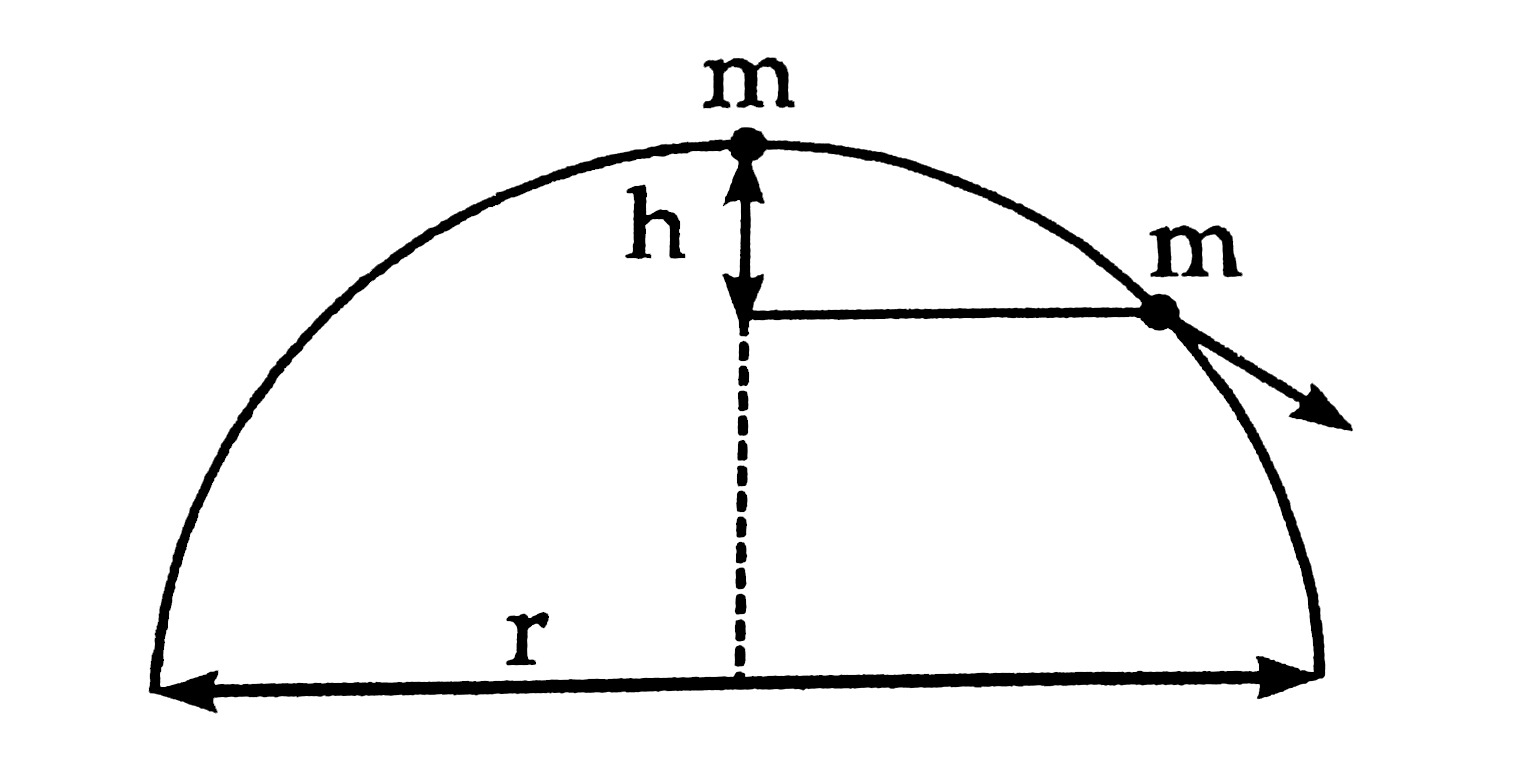
A small body of mass m slides down from the top of a hemisphere of radius r . The surface of block and hemisphere are frictionless. The height at which the body lose contact with the surface of the sphere is

32R
23R
12R
13R
(b) Suppose body slips at point B
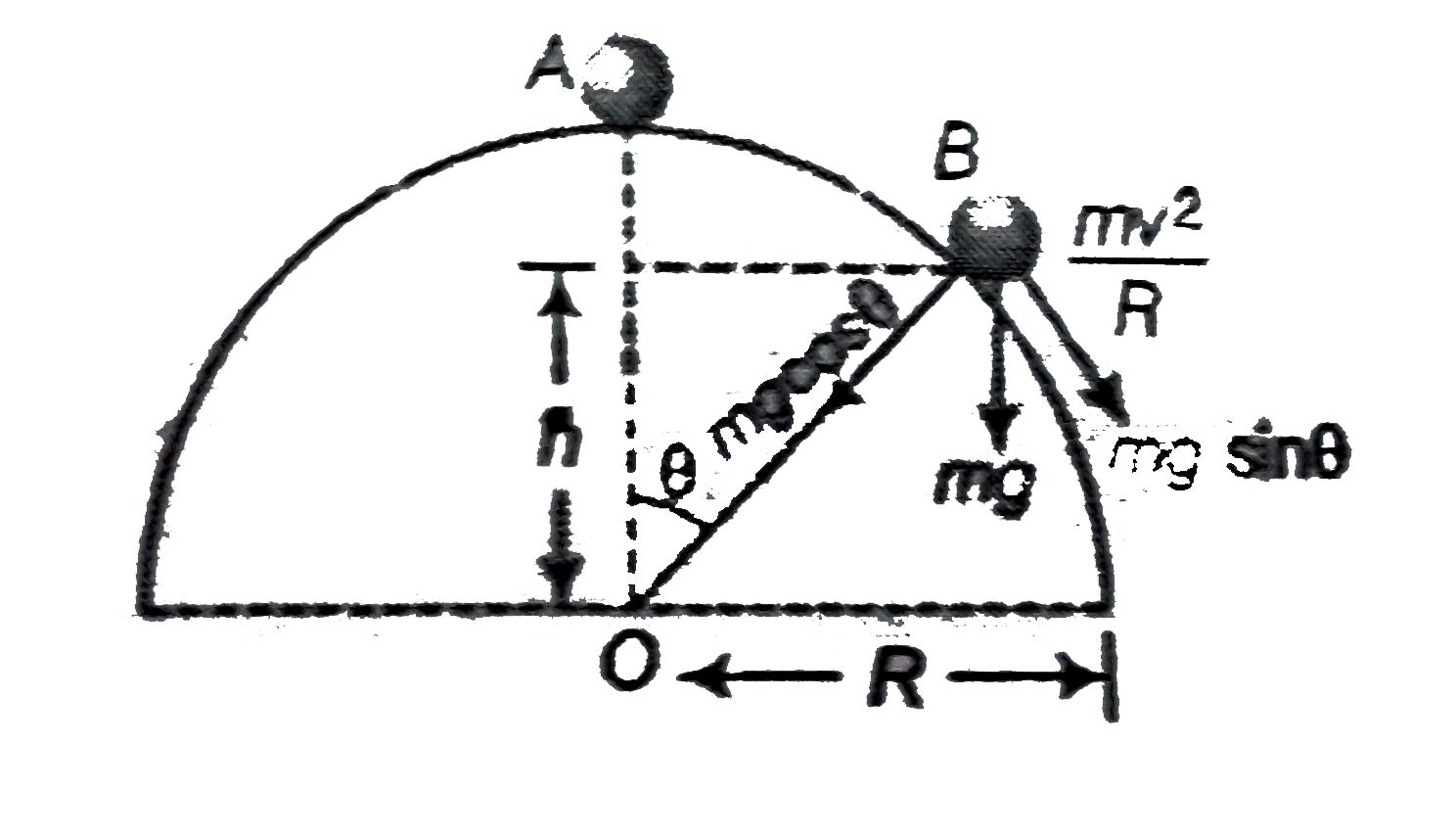
mgcosθ=mv2R[v=√2g(R−h)]
gcostheta=(2g(R-h))/(R)<br>costheta=(2(R-h))/(R)<br>(h)/(R)=(2(R-h))/(R)" " [costheta=(h)/(R)]<br>:." "h=(2)/(3)R
Topper's Solved these Questions
Similar Questions
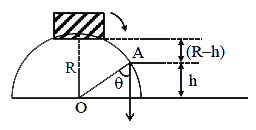
A small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
View SolutionA small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?
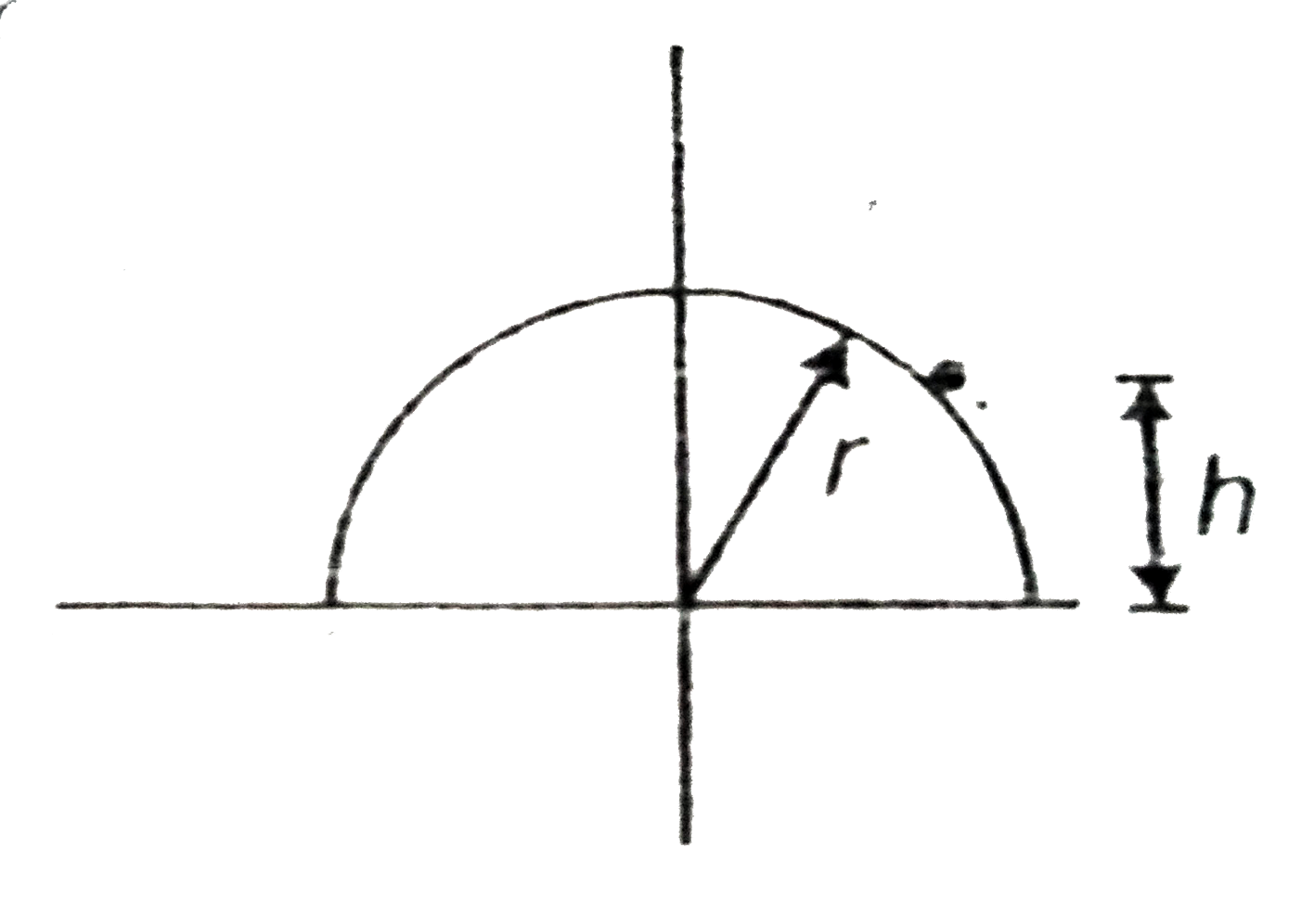
View Solution
Knowledge Check
The total surface area of a solid hemisphere of radius r is
Aπr2B2πr2C3πr2D4πr2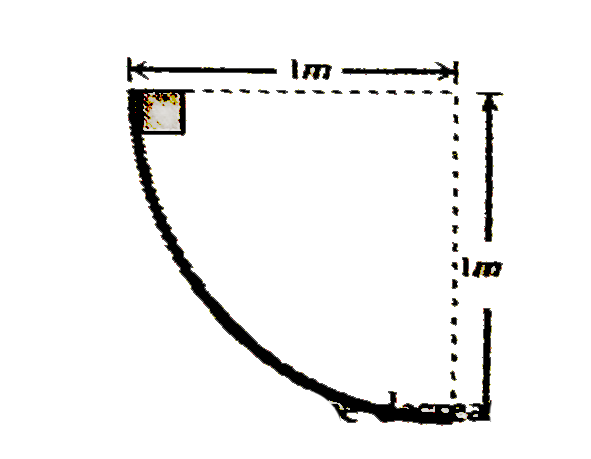
A body of mass 2kg slides down a curved track which is quadrant of a circle of radius 1 metre . All the surfaces are frictionless. If the body starts from rest, its speed at the bottom of the track isA4.43m/secB2m/secC0.5m/secD19.6m/ec
A small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View SolutionWhat is the total surface area of hemisphere if the radius of hemisphere is r.
View SolutionA small body A starts sliding off the top of a smooth sphere of radius R. Find the angle θ (figure) corresponding to the point at which the body breaks off the sphere, as well as the break-off velocity of the body.

View SolutionFind the ratio of the total surface area of a sphere and a hemisphere of same radius.
View SolutionA particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical wheere cosθ35. if the work done against frictiion is 2mgR10x, find x.
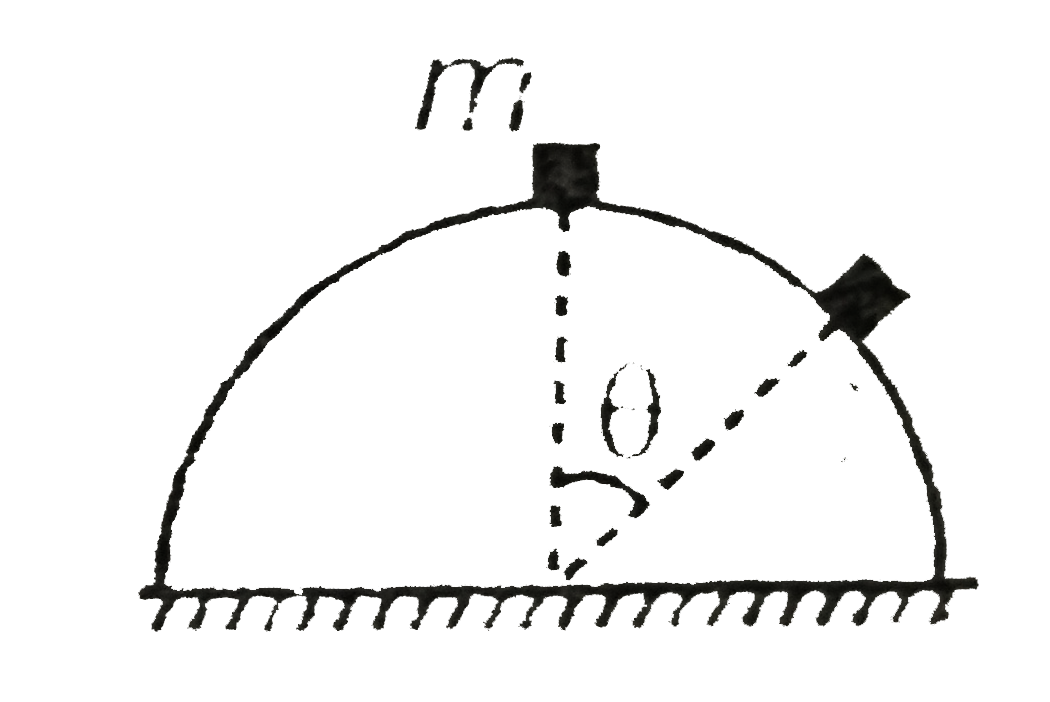
View Solution
