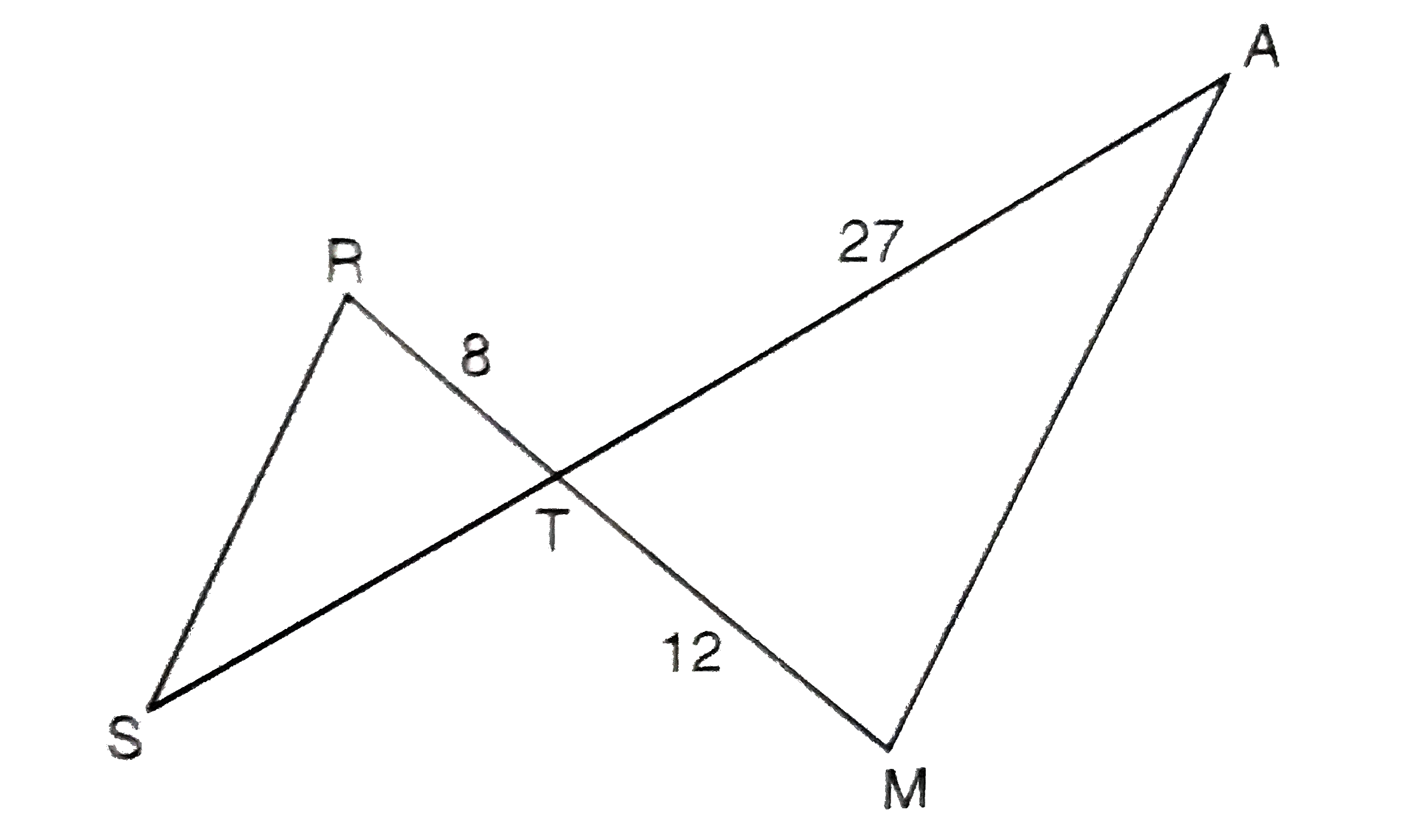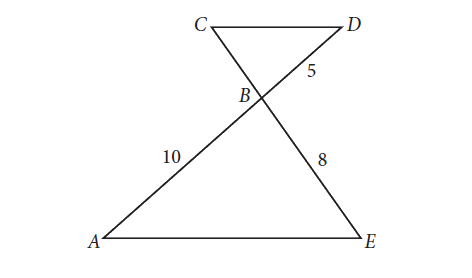
In the figure above, AE || CD and segment AD intersects segment CE at B. What is the length of segment CE ?
Video Solution
Text Solution
The correct answer is 12. Angles ABE and DBC are vertical angles and thus have the same measure. Since segment AE is parallel to segment CD, angles A and D are of the same measure by the alternate interior angle theorem. Thus, by the angle-angle theorem, triangle ABE is similar to triangle DBC, with vertices A, B, and E corresponding to vertices D, B, and C, respectively. Thus, ABDB=EBCBor105=8CB . It follows that CB = 4, and so CE=CB+BE=4+8=12.
|
Similar Questions
Knowledge Check

In the figure above, if line segment AB is parallel to line segment CD, what is the value of y?A12B15C18D20In the figure above, if VO=VY, what is the slope of segment VO?
A−√3B−√32C√32Dcannot be determined from the given informationIn the circle shown in the figure, the length of the arc ACB is 3 times the length of the arc AB. What is the length of the line segment AB ?
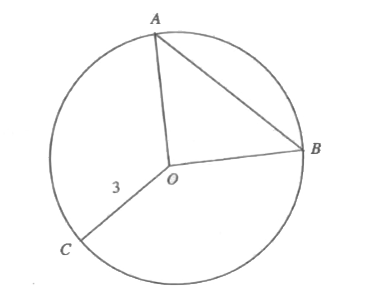 A3B4C5D3√2
A3B4C5D3√2
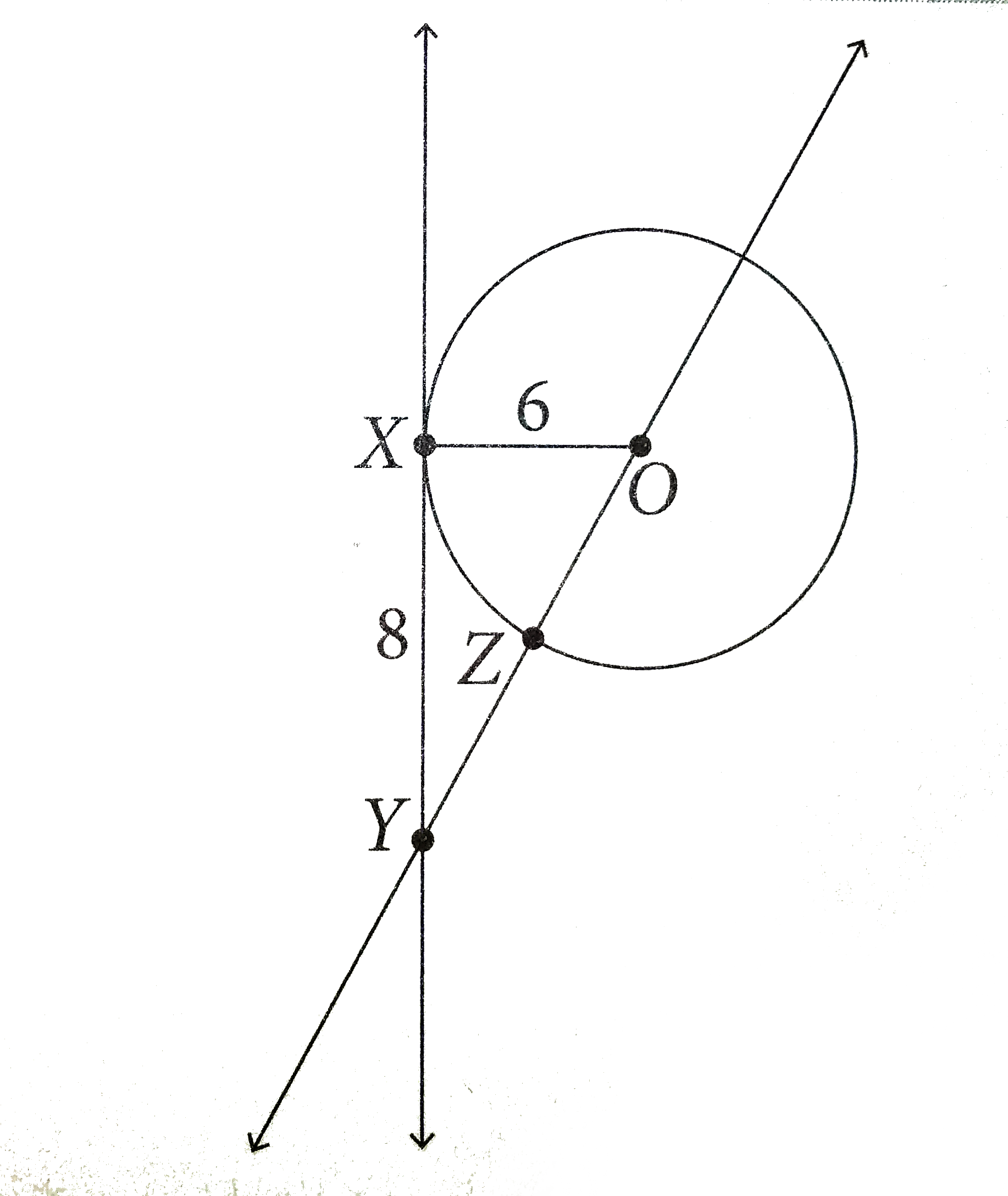
In the figure above, O is the center of the circle, the length of segment XY is 8, and the line passing through point X and Y is tangent to the circle at point X. What is the length of segment ZY?
View Solution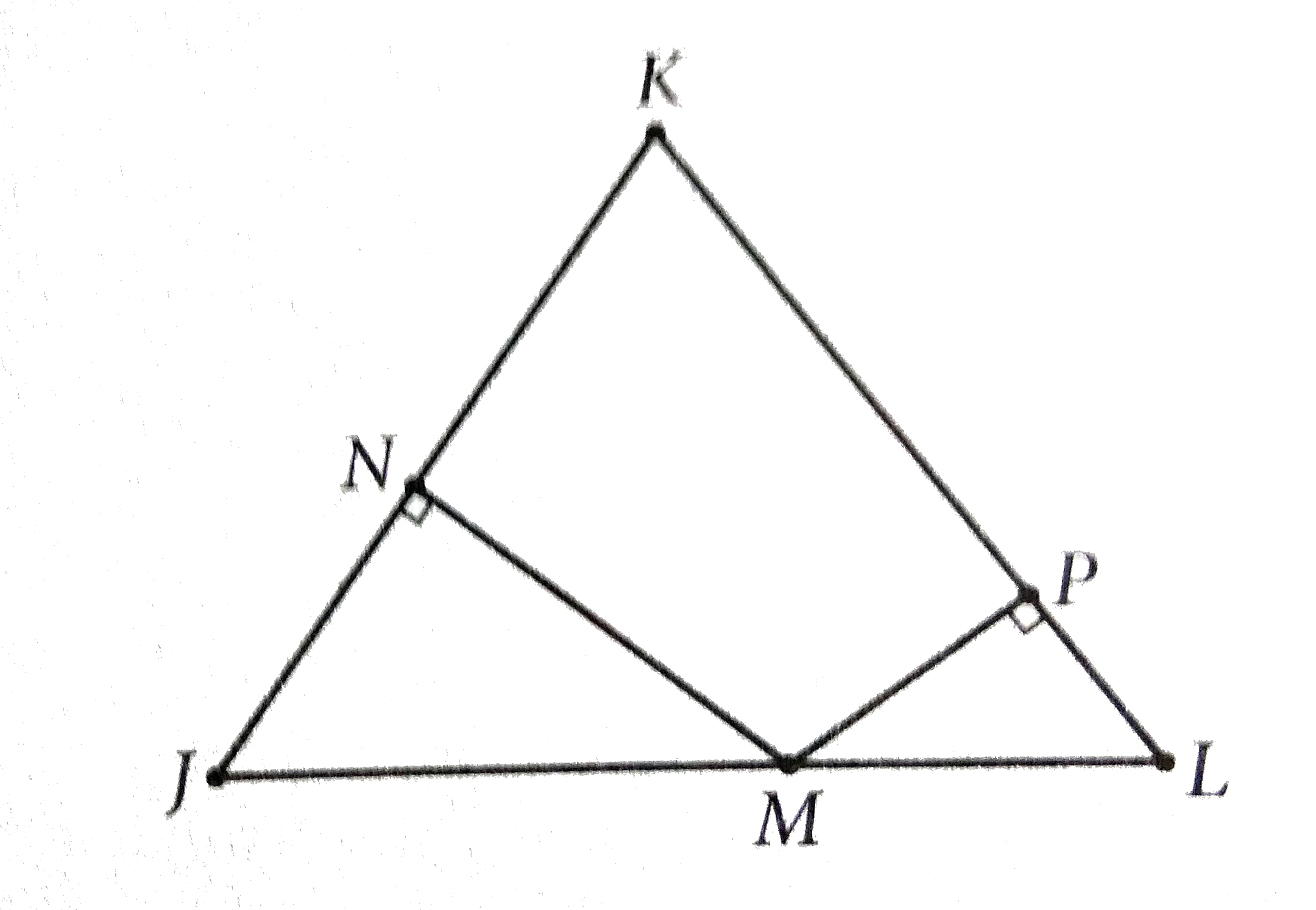
In triangle JKL above, JK=KLandJL=26. The ratio of MN to MP is 8.5. What is the length of segment JM?
View SolutionIn the given figure, AB∣∣CD. The line segments BC and AD intersect at O. Show that : z=x+y.

View Solution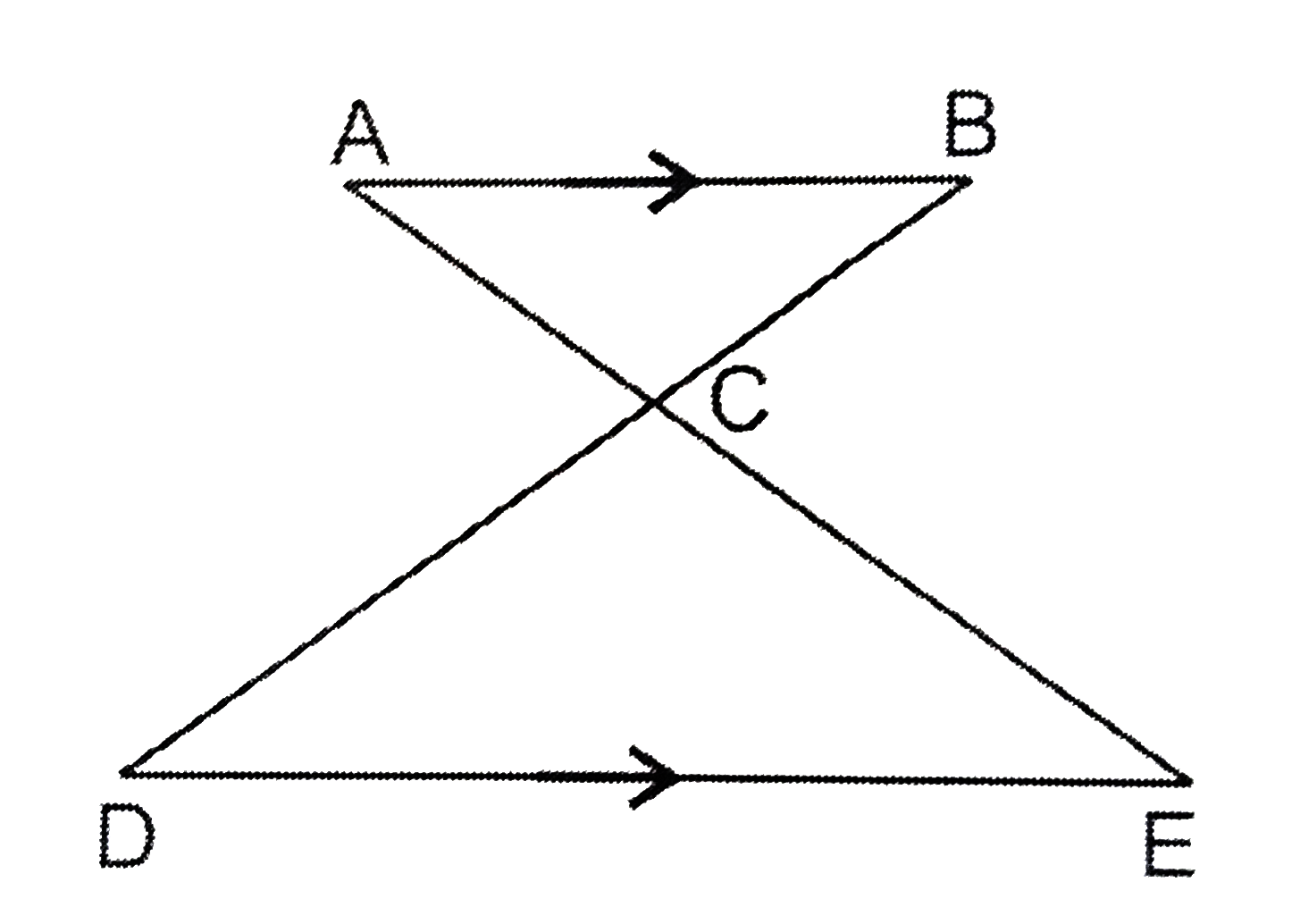
In the figure AB∣∣DE , AC=6, CE=15 and DB=28. What is the length of CD?
View Solution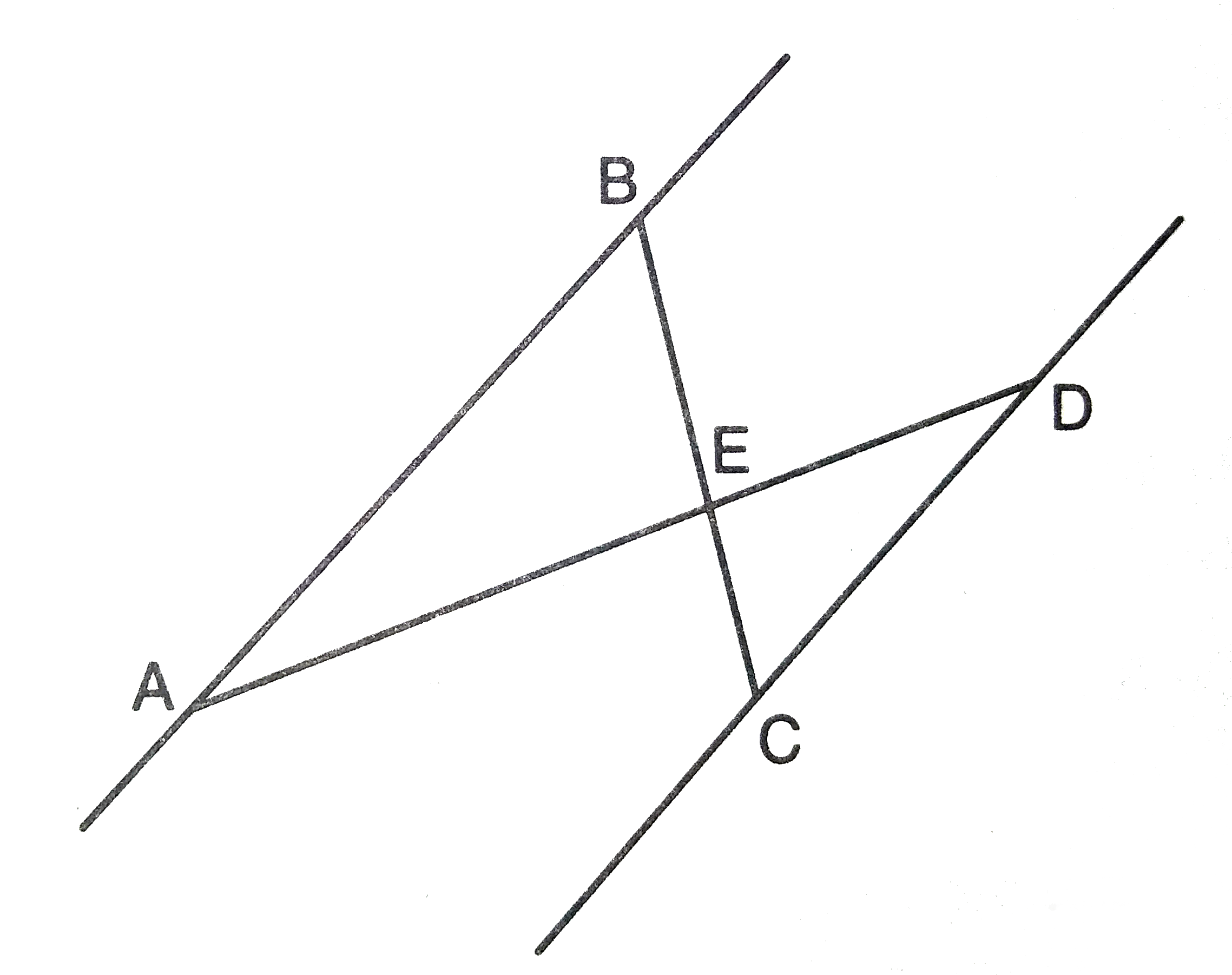
In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD, AD=30, AB=21, and CD=15. What is the length of ¯¯¯¯¯¯DE?
View Solution