f(x)=(x+6)(x−4)
Which of the following is an equivalent form of the function f above in which the minimum value of f appears as a constant or coefficient?
f(x)=x2−24
f(x)=x2+2x−24
f(x)=(X−1)2−21
f(x)=(x+1)2−25
The correct Answer is:D
To solve the problem, we need to rewrite the function f(x)=(x+6)(x−4) in a form that highlights its minimum value. We will follow these steps:
Step 1: Expand the function
First, we will expand the function f(x).
f(x)=(x+6)(x−4)
Using the distributive property (FOIL method):
f(x)=x2−4x+6x−24
Combining like terms:
f(x)=x2+2x−24
First, we will expand the function f(x).
Similar Questions
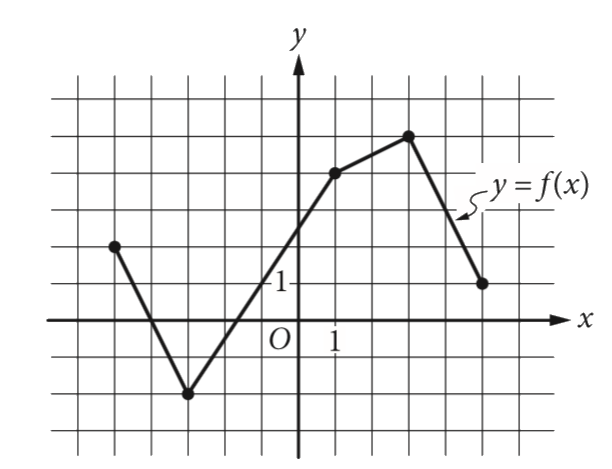
The complete graph of the function f is shown in the xy-plane above. For what value of x is the value of f(x) at its minimum?
View Solutiong(x)=(x−5)(x+3)
Which of the following is an equivalent form of the function g above in which the minimum value of g appears as a constant or coefficient ?
View SolutionLet f be a real-valued function satisfying f(x)+f(x+4)=f(x+2)+f(x+6) Prove that ∫x+8xf(t)dt is constant function.
View SolutionThe minimum value of the function f(x)=tan(x+π6)tanx is:
View SolutionThe function f (x) is differentiable for every x. f(1)=−2 and f'(x)≥2,∀x∈[1,6]. Then minimum value of f (6) is ……….
View SolutionA function f is such that f'(4)=f''(4)=0 and f has minimum value 10 at x=4. Then f(x) is equal to
View SolutionA polynomial function f(x) is such that f'(4)= f''(4)=0 and f(x) has minimum value 10 at x=4 .Then
View SolutionLet f be a real-valued function satisfying f(x)+f(x+4)=f(x+2)+f(x+6) Prove that ∫x+8xf(t)dt is constant function.
View Solution
