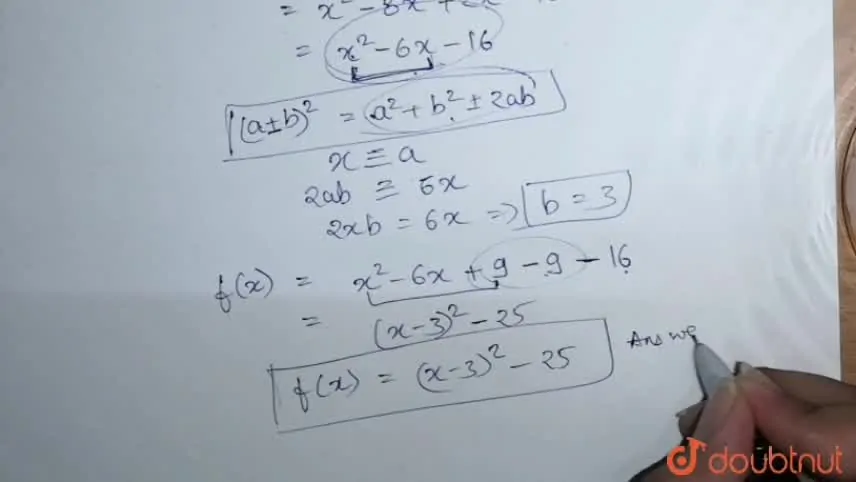f(x)=(x−8)(x+2)
f(x)=x2−16
f(x)=(x+3)2−16
f(x)=(x+3)2−7
f(x)=(x−3)2−25
The correct Answer is:D
Step by step video, text & image solution for f(x)=(x-8)(x+2) ,brgt Which of the following is an equivalent form of the function above in which the minimum value of function f appears in the equation as a constant? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
g(x)=(x−5)(x+3)
Which of the following is an equivalent form of the function g above in which the minimum value of g appears as a constant or coefficient ?View Solutionf(x)=(x+6)(x−4)
Which of the following is an equivalent form of the function f above in which the minimum value of f appears as a constant or coefficient?View SolutionThe graph of the function f(x)=−12(x+4)(x+8) in the xy-plane is a parabola. Which of the following is an equivalent form of function f in which the maximum value of the function appears as a constant?
View Solutiony=x2+16x+28
The equation above represents the graph of a parabola in the xy-plane. Which of the following represents an equivalent form of the equation that includes the minimum value of y as a constant?View SolutionThe minimum value of the function f(x)=tan(x+π6)tanx is:
View Solutionf(x)=x4+2x3−3x2+4x+12x+3
Which of the following functions is equivalent to the functions above for all values of x for which function above for all values of x for which function f is defined?View SolutionFor which of the following functions does f(x)f(2−x) ?
View SolutionFind the maximum and minimum values of the function f(x)=tanx−2x .
View SolutionLet f(x) = [x] and g(x) = x - [x], then which of the following functions is the zero function ?
View Solutionf(x)=x+32
For the function f defined above, what is the value of f (−1) ?View Solution