In the equation above, t is a constant. If the equation has no real solutions, which of the following could be the value of t ?
3
The correct Answer is:A
To determine the value of t for which the equation 2x2−4x=t has no real solutions, we need to analyze the quadratic equation formed by rearranging it into standard form.
1. Rearranging the equation:
Start with the given equation:
2x2−4x−t=0
This is now in the standard quadratic form ax2+bx+c=0, where:
- a=2
- b=−4
- c=−t
Hint: Identify the coefficients a, b, and c from the standard form of a quadratic equation.
2. Using the discriminant:
For a quadratic equation to have no real solutions, the discriminant must be less than zero. The discriminant D is given by:
D=b2−4ac
Substituting the values of a, b, and c:
D=(−4)2−4⋅2⋅(−t)
Hint: Remember that the discriminant determines the nature of the roots of the quadratic equation.
3. Calculating the discriminant:
Calculate D:
D=16+8t
We want this discriminant to be less than zero for the equation to have no real solutions:
16+8t<0
Hint: Set up the inequality to find the conditions on t.
4. Solving the inequality:
Rearranging the inequality gives:
8t<−16
Dividing both sides by 8:
t<−2
Hint: Isolate t to find the range of values that satisfy the condition.
5. Finding possible values of t:
Now, we need to find a value of t that is less than -2. For example, t=−3 satisfies this condition.
Hint: Check the options provided to see which values are less than -2.
Conclusion:
The value of t that could make the equation 2x2−4x=t have no real solutions is t=−3.
Start with the given equation:
2x2−4x−t=0
This is now in the standard quadratic form ax2+bx+c=0, where:
- a=2
- b=−4
- c=−t
For a quadratic equation to have no real solutions, the discriminant must be less than zero. The discriminant D is given by:
D=b2−4ac
Substituting the values of a, b, and c:
D=(−4)2−4⋅2⋅(−t)
Calculate D:
D=16+8t
We want this discriminant to be less than zero for the equation to have no real solutions:
16+8t<0
Rearranging the inequality gives:
8t<−16
Dividing both sides by 8:
t<−2
Now, we need to find a value of t that is less than -2. For example, t=−3 satisfies this condition.
The value of t that could make the equation 2x2−4x=t have no real solutions is t=−3.
Similar Questions
Knowledge Check
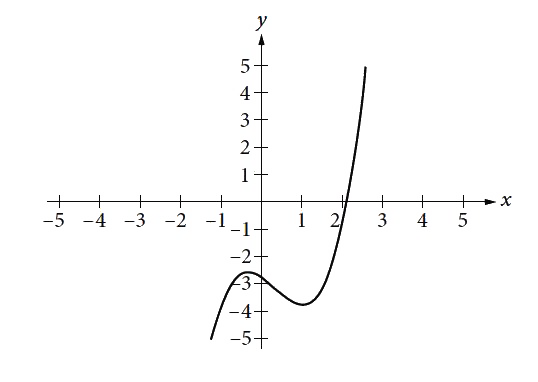
The function f(x)=x3−x2−x−114 s graphed in the xy-plane above. If k is a constant such that the equation f(x)=k has three real solutions, which of the following could be the value of k ?A2B0C−2D−3If 8and−4 are the solutions for x, which of the following could be the equation?
Ax2−4x−32=0Bx2−4x+32=0Cx2+4x−12=0Dx2+4x+32=0(2x2+3x−4)(3x+2)=6x3+ax2−6x−8
In the above equation, a is a constant. If the equation is true for all value of x, what is the value of a ?A4B9C13D16
4x2−9=(px+t)(px−t)
In the equation above, p and t are constants. Which of the following could be the value of p ?
View Solutionx(dx+10)=−3
The equation above, where d is a constant, has no real solutions. The value of d could be which of the following?
View Solution{(y=(1)/(2)x-2), (y=-x^(2)+1):}
If (a, b) is a solution to the system of equations above, which of the following could be the value of b?
View Solution−3x + y = 6
ax + 2y = 4
In the system of equations above, a is a constant. For which of the following values of a does the system have no solution?
View Solution12t+4=34t−5
In the equation above . What is the value of t?
View Solution
