An electron moves a distance of 6.0 cm when accelerated from rest by an electric field of strength 2×10−4NC−1. Calculate the time of travel.
The correct Answer is:5.85×10−5s
To solve the problem of an electron moving a distance of 6.0 cm when accelerated from rest by an electric field of strength 2×10−4N/C, we will follow these steps:
Step 1: Identify the given values
- Distance S=6.0cm=6.0×10−2m
- Electric field strength E=2×10−4N/C
- Charge of electron Q=1.6×10−19C
- Mass of electron m=9.1×10−31kg
Step 2: Calculate the force acting on the electron
The force F acting on the electron due to the electric field is given by:
F=Q×E
Substituting the values:
F=(1.6×10−19C)×(2×10−4N/C)=3.2×10−23N
Step 3: Calculate the acceleration of the electron
Using Newton's second law, the acceleration A can be calculated as:
A=Fm
Substituting the values:
A=3.2×10−23N9.1×10−31kg≈3.51×107m/s2
Step 4: Use the kinematic equation to find the time of travel
Since the electron starts from rest, the initial velocity U=0. The kinematic equation relating distance, initial velocity, acceleration, and time is:
S=UT+12AT2
Substituting U=0:
S=12AT2
Rearranging for T:
T2=2SA
T=√2SA
Step 5: Substitute the values to find T
Substituting S=6.0×10−2m and A≈3.51×107m/s2:
T=√2×(6.0×10−2)3.51×107
Calculating the values:
T=√1.2×10−13.51×107≈√3.42×10−9≈5.84×10−5s
Final Answer
The time of travel for the electron is approximately T≈5.84×10−5s.
---
- Distance S=6.0cm=6.0×10−2m
- Electric field strength E=2×10−4N/C
- Charge of electron Q=1.6×10−19C
- Mass of electron m=9.1×10−31kg
The force F acting on the electron due to the electric field is given by:
F=Q×E
Substituting the values:
F=(1.6×10−19C)×(2×10−4N/C)=3.2×10−23N
Using Newton's second law, the acceleration A can be calculated as:
A=Fm
Substituting the values:
A=3.2×10−23N9.1×10−31kg≈3.51×107m/s2
Since the electron starts from rest, the initial velocity U=0. The kinematic equation relating distance, initial velocity, acceleration, and time is:
S=UT+12AT2
Substituting U=0:
S=12AT2
Rearranging for T:
T2=2SA
T=√2SA
Substituting S=6.0×10−2m and A≈3.51×107m/s2:
T=√2×(6.0×10−2)3.51×107
Calculating the values:
T=√1.2×10−13.51×107≈√3.42×10−9≈5.84×10−5s
The time of travel for the electron is approximately T≈5.84×10−5s.
Similar Questions
An electron falls through a distance 1.5 cm in a uniform electric field of magnitude 2.0×104NC−1 .Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed keeping its magnitude uncharged , calculate the time taken by a proton to fall through this distance starting from rest.
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
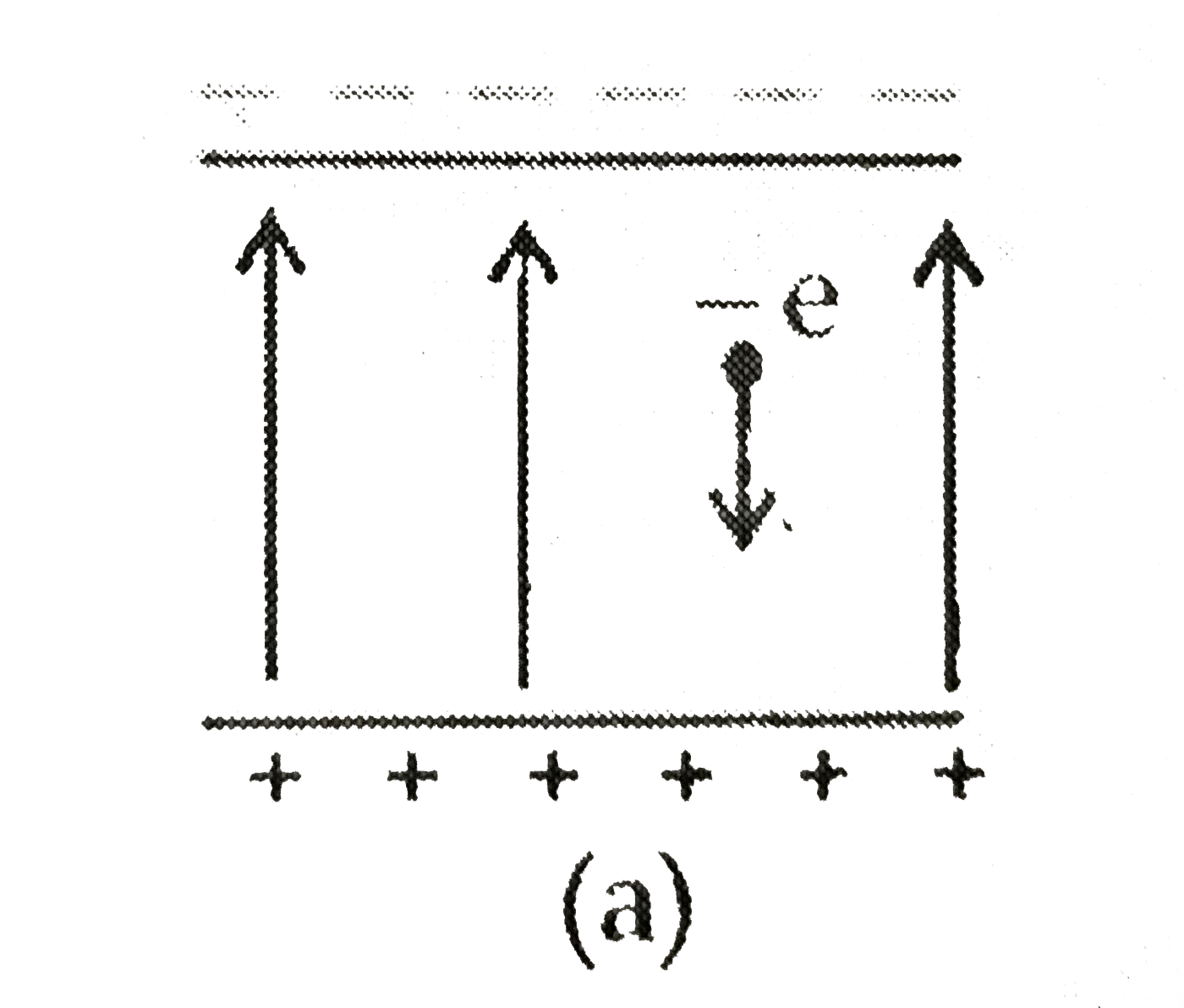
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest.

View Solution
Knowledge Check
An electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E the velocity acquired by it as it travels a distance l is
A[2Eqlm]1/2B[2EqmI]1/2C[2Emql]1/2D[EqmI]1/2An electron of mass m and charge q is accelerated from rest in a uniform electric field of strength E. The velocity acquired by it as it travels a distance l is
A√2Eql/mB√2Eq/mlC√2Em/qlD√Eq/mlAn electron initially at rest falls a distance of 2 cm in a uniform electric field of magnitude 3×104NC−1. The time taken by the electron to fall to this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.75×10−9s
A small metallic ball with charge 1 μC and mass 0.1 mg, when thrown in an upward direction with initial velocity u, comes to rest after covering a distance of 5 cm in a uniform external electric field of strength 2.8×106NC−1 . Find the value of u.
View SolutionAn electron is released from rest in a uniform electric field of magnitude 2.00×104N/C . (a) Calculate the acceleration of the electron. (Ignore gravitational) (b) How much time does the electron take to reach 1.00 % of the speed of light ?
View SolutionAn electric dipole consists of charges +2eand−2e separated by 0.78mm. It is an electric field of strength 3.4×106N/C. Calculate the magnitude of the torque on the dipole when the dipole moment is (a) parallel to (b) perpendicular to, and (c) antiparallel to the electric field.
View SolutionAn electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View SolutionA diople consisting of an electron and a proton separated by a distance of 4×10−10 m is situated in an electric field of intensity 3×105NC−1 at an angle of 30∘ with the field. Calculate the diople moment and the torque acting on it. Charge e on an electron =1⋅6×10−19C.
View Solution

