An electron is liberated from the lower of the two large parallel metal plates separated by a distance of 20 mm. the upper plate has a potential of +2400V relative to the lower plate. How long does the electron take to reach the upper plate ? Take em of electrons 1.8×1011Ckg−1
To solve the problem of how long it takes for an electron to reach the upper plate of a parallel plate capacitor, we can follow these steps:
Step 1: Understand the Setup
We have two parallel plates separated by a distance D=20mm=20×10−3m. The upper plate has a potential of V=+2400V and the lower plate is at 0V. An electron is liberated from the lower plate and moves towards the upper plate.
Step 2: Calculate the Electric Field (E)
The electric field E between two parallel plates is given by the formula:
E=VD
Substituting the values:
E=2400V20×10−3m=24000.02=120000V/m
Step 3: Calculate the Force (F) on the Electron
The force F acting on the electron due to the electric field is given by:
F=eE
Where e is the charge of the electron (e≈1.6×10−19C). Thus:
F=(1.6×10−19C)(120000V/m)=1.92×10−14N
Step 4: Calculate the Acceleration (a) of the Electron
Using Newton's second law, the acceleration a of the electron can be calculated as:
a=Fm
Where m is the mass of the electron (m≈9.11×10−31kg). Therefore:
a=1.92×10−14N9.11×10−31kg≈2.11×1016m/s2
Step 5: Use Kinematic Equation to Find Time (t)
Since the electron starts from rest, we can use the kinematic equation:
S=ut+12at2
Where S=D=20×10−3m and u=0. This simplifies to:
D=12at2
Rearranging gives:
t2=2Da
Substituting the known values:
t2=2(20×10−3m)2.11×1016m/s2≈0.042.11×1016≈1.895×10−18
Taking the square root:
t≈√1.895×10−18≈1.38×10−9s
Final Answer
The time taken by the electron to reach the upper plate is approximately:
t≈1.38ns(nanoseconds)
---
We have two parallel plates separated by a distance D=20mm=20×10−3m. The upper plate has a potential of V=+2400V and the lower plate is at 0V. An electron is liberated from the lower plate and moves towards the upper plate.
The electric field E between two parallel plates is given by the formula:
E=VD
Substituting the values:
E=2400V20×10−3m=24000.02=120000V/m
The force F acting on the electron due to the electric field is given by:
F=eE
Where e is the charge of the electron (e≈1.6×10−19C). Thus:
F=(1.6×10−19C)(120000V/m)=1.92×10−14N
Using Newton's second law, the acceleration a of the electron can be calculated as:
a=Fm
Where m is the mass of the electron (m≈9.11×10−31kg). Therefore:
a=1.92×10−14N9.11×10−31kg≈2.11×1016m/s2
Since the electron starts from rest, we can use the kinematic equation:
S=ut+12at2
Where S=D=20×10−3m and u=0. This simplifies to:
D=12at2
Rearranging gives:
t2=2Da
Substituting the known values:
t2=2(20×10−3m)2.11×1016m/s2≈0.042.11×1016≈1.895×10−18
Taking the square root:
t≈√1.895×10−18≈1.38×10−9s
The time taken by the electron to reach the upper plate is approximately:
t≈1.38ns(nanoseconds)
Topper's Solved these Questions
- ELECTROSTATIC FORCES, CHARGES AND FIELDSBook:SL ARORAChapter:ELECTROSTATIC FORCES, CHARGES AND FIELDSExercise:Problems
Explore 18 Videos
- ELECTROSTATIC FORCES, CHARGES AND FIELDSBook:SL ARORAChapter:ELECTROSTATIC FORCES, CHARGES AND FIELDSExercise:Problems For Self Practice
Explore 1 Video
- ELECTRONS AND PHOTONSBook:SL ARORAChapter:ELECTRONS AND PHOTONSExercise:TYPE E : Problem For Self Practice
Explore 11 Videos
- HEATING EFFECT OF CURRENTBook:SL ARORAChapter:HEATING EFFECT OF CURRENTExercise:All Questions
Explore 192 Videos
Similar Questions
Two parallel plates kept in air 5cm apart are at a potential difference of 500V. If there be an electron (ii) kinetic energy an (iii) velocity of the electron, when it reaches the other plate.
View SolutionCalculate the capacitance of a parallel-plate capacitor having 20 cm xx 20 cm square plates separated by a distance of 1.0 mm.
View Solution
Knowledge Check
An electron having charge e and mass m starts from the lower plate of two metallic plates separated by a distance d. If the potential difference between the plates is V, the time taken by the electron to reach the upper plate is given by
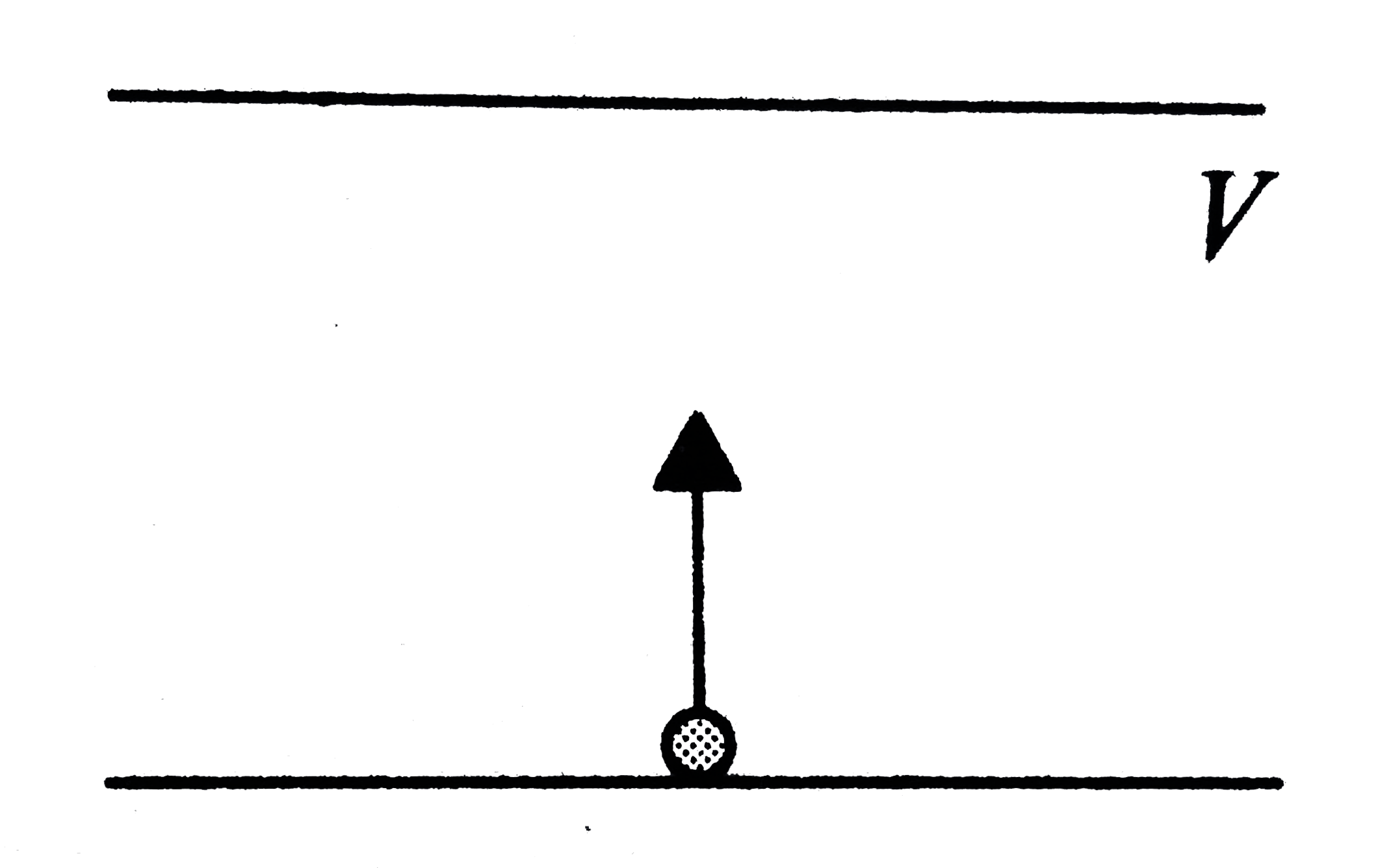 .A√2md2eVB√md2eVC√md22eVD2md2eV
.A√2md2eVB√md2eVC√md22eVD2md2eVThe p.d between two plates separated by a distance of 1mmis100V.The force on an electron placed in between the plates is
A105NB1.6×10−24NC1.6×10−14ND1.6×10−19NAn electron enters between two horizontal plates separated by 2mm and having a potential difference of 1000V. The force on electron is
A8×10−12NB8×10−14NC8×10−9ND8×1014N
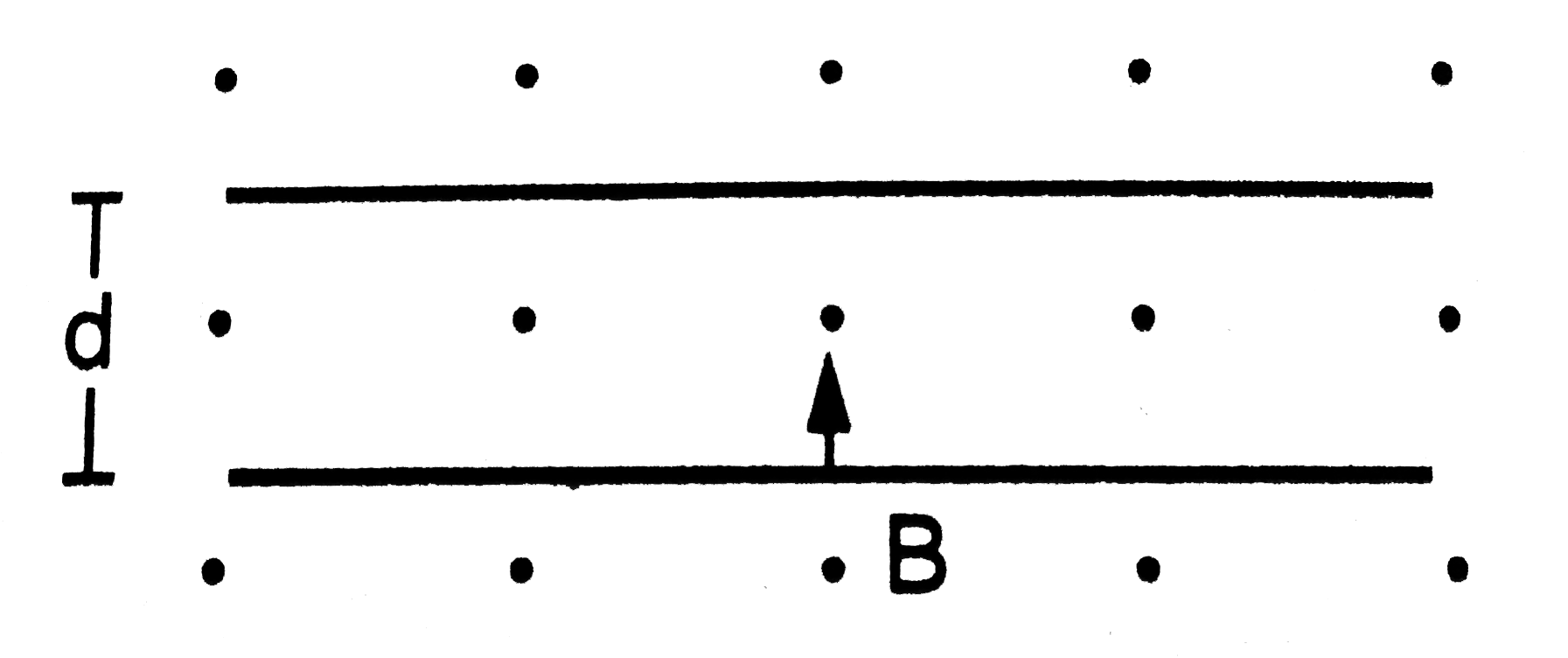
An electron is emitted with negligible speed from th nagative plate of a parallel plate capacitor charged ot a potential difference V. The separtion between the plates is d and a magnetic field B exists in the space as shown in . Show that the electron will fail to strike the upper plate if ltdgt (2meVeB20)12.
View SolutionAn electric field E is produced between two parallel plates having a separation d as shown.
(a) With what minimum speed should an electron be projected from the lower plate in the direction of field so that it may reach the upper plate ?
(b) Suppose the electron is projected from the lower plate with the speed calculated in part (a). The direction of projection makes an angle of 60∘with the field. Find the maximum height reached by the electron.
(c ) After how much time , the electron again strikes the lower plate ?
(d) Horizontal distance travelled by the electron in time calculated in part (c).
Charge on electron : e ,mass of electron : m, consider only electric force.
View SolutionA partical having charge that of an electron and mass 1.6×10−30kg is projected with an initial speed u at the angle 45∘ to the horizontal from the lower plate of a parallel-plate capacitor as shown in fig. The plates are suffiecienly long and have a separation of 2 cm, find the maximum value of the velocity of he particle so that it does not hit the upper plate. Take the electric field between the plates as 103Vm−1 directed upward.

View Solution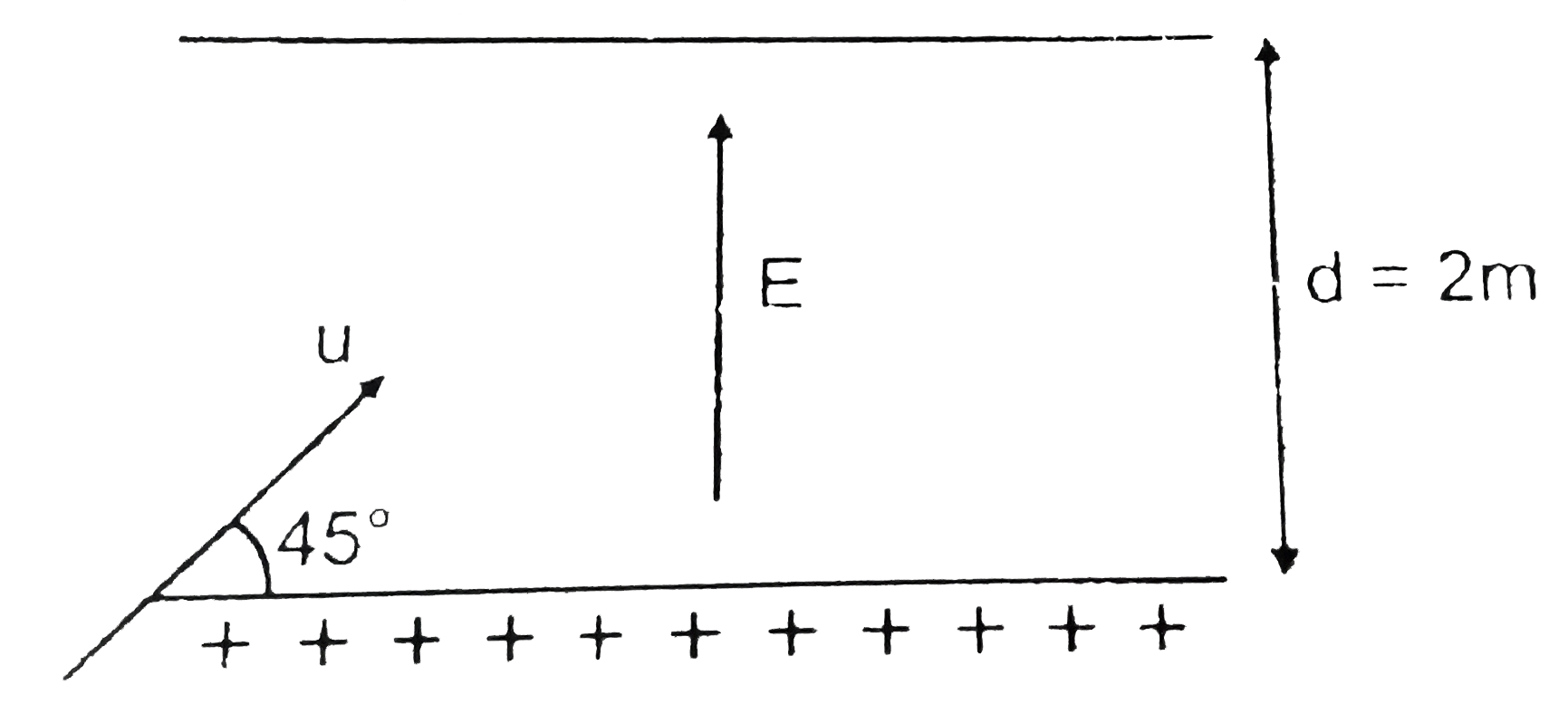
An electron is projected as shown with speed u. If electron just fails to strike the upper plate, find range. (distance from starting point at which electron strike the lower plate again). Consider only electric force.
View SolutionElectrons are observed to be ejected in various directions with negligible speed from the negative plate of a parallel plate capacitor when the plate is illuminated by a certain wavelength. The plates are separated by a distance d and a potential difference V is maintained between them. Show that none of these electrons will reach the positive plate if a magnetic field is applied at right angles to the electric field and that the magnetic induction has a value B>(2mVed2)12 where m and e are the electron mass and charge respectively.
View Solution

