A particle moves in space along the path z=ax3+by2 in such a way that dxdt=c=dydt where a,b and c are constants. The acceleration of the particle is
(6ac2x+2bc2)ˆk
(2ax2+6by2)ˆk
(4bc2+3ac2)ˆk
(bc2x+2by)ˆk
The correct Answer is:A
Step by step video, text & image solution for A particle moves in space along the path z=ax^(3)+by^(2) in such a way that (dx)/(dt)=c=(dy)/(dt) where a,b and c are constants. The acceleration of the particle is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A particle moves along a path y=ax2 (where a is constant) in such a way that x-component of its velocity (ux) remains constant. The acceleration of the particle is
View SolutionA particle moves along the parabola y2=2ax in such a way that its projection on y-axis has a constant velocity. Show that its projection on the x-axis moves with constant acceleration
View Solution
Knowledge Check
The displacement x of a particle at time t moving along a straight line path is given by x2=at2+2bt+c where a, b and c are constants. The acceleration of the particle varies as
Ax−1Bx−2Cx−3Dx−4A particle moves along a parabolic parth y=9x2 in such a way that the x-component of velocity remains constant and has a value 13ms−1 . The acceleration of the particle is -
A13ˆlms−2B3ˆjms−2C23ˆjms−2D2ˆjms−2A particle moves along the parabolic path y=ax2 in such a The accleration of the particle is:
A2a2cˆjB2ac2ˆjCacˆkDa2c2ˆk
A particle moves uniformly with speed v along a parabolic path y=kx2, where k is a positive constant. Find the acceleration of the particle at the point x = 0.
View SolutionThe angular acceleration of a particle moving along a circle is given by a=ksin (theta),where "theta" is the angle turned by particle and k is constant.The centripetal acceleration of the particle in terms of k ,theta and R (radius of circle) is given by
View SolutionA particle moves along a constant curvature path between A and B (length of curve wire AB is 100m) with a constant speed of 72km/hr. The acceleration of particle at mid point 'C' of curve AB is
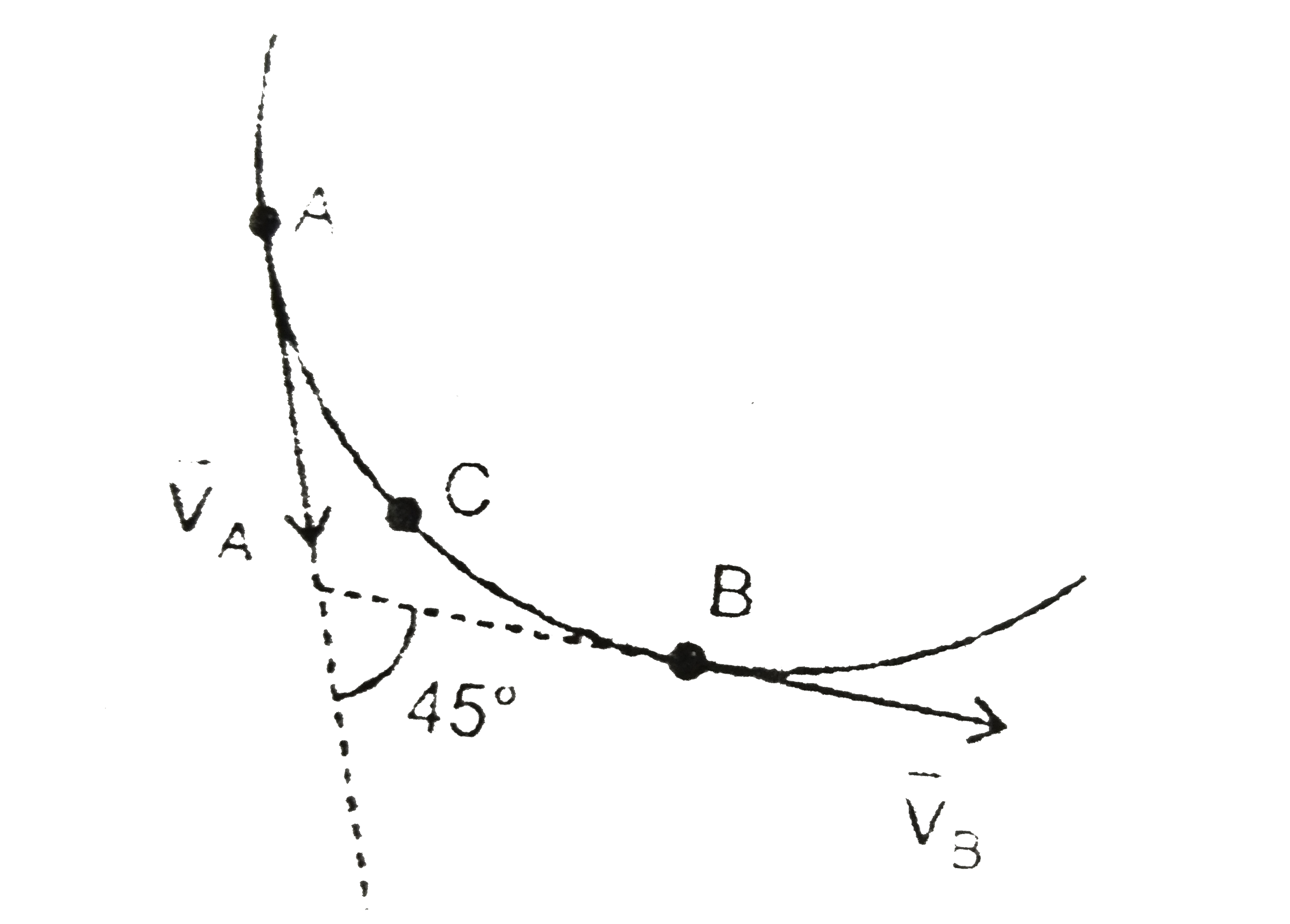
View SolutionDisplacement (x) of a particle is related to time (t) as
x=at+bt2−ct3
where a,b and c are constant of the motion. The velocity of the particle when its acceleration is zero is given by:
View SolutionA particle moves along a straight line to follow the equation ax2+bv2=k, where a,b is and k are constant and x and and x axis coordirete and velocity of the particle respectively find the amplitude
View Solution
