Two particles are released from the same height at an interval of 1s. How long after the first particle begins to fall will the two particles be 10m apart? (g=10m/s2)
1.5s
2s
1.25s
2.5s
The correct Answer is:A
To solve the problem, we need to determine how long after the first particle begins to fall the two particles will be 10 meters apart.
1. Understanding the Problem:
- Particle 1 is released at time t=0.
- Particle 2 is released at time t=1 second.
- We need to find the time t after the release of Particle 1 when the distance between the two particles is 10 meters.
2. Using the Equations of Motion:
- The distance fallen by an object under gravity (with initial velocity u=0) is given by the equation:
s=ut+12gt2
- For both particles, since they are released from rest, the equation simplifies to:
s=12gt2
3. Calculating the Distance Fallen by Each Particle:
- For Particle 1 (released at t=0):
- At time t, the distance fallen is:
H1=12gt2
- For Particle 2 (released at t=1):
- At time t, the time since its release is t−1. Thus, the distance fallen is:
H2=12g(t−1)2
4. Setting Up the Equation:
- According to the problem, the distance between the two particles is 10 meters:
H1−H2=10
- Substituting the expressions for H1 and H2:
12gt2−12g(t−1)2=10
5. Simplifying the Equation:
- Factor out 12g:
12g(t2−(t−1)2)=10
- Expanding (t−1)2:
(t−1)2=t2−2t+1
- Therefore:
t2−(t2−2t+1)=2t−1
- Substituting back:
12g(2t−1)=10
6. Substituting g=10m/s2:
- Plugging in the value of g:
12×10(2t−1)=10
- Simplifying:
5(2t−1)=10
- Dividing both sides by 5:
2t−1=2
- Solving for t:
2t=3⇒t=32=1.5seconds
Final Answer:
The two particles will be 10 meters apart after 1.5 seconds from the release of the first particle.
---
- Particle 1 is released at time t=0.
- Particle 2 is released at time t=1 second.
- We need to find the time t after the release of Particle 1 when the distance between the two particles is 10 meters.
- The distance fallen by an object under gravity (with initial velocity u=0) is given by the equation:
s=ut+12gt2
- For both particles, since they are released from rest, the equation simplifies to:
s=12gt2
- For Particle 1 (released at t=0):
- At time t, the distance fallen is:
H1=12gt2
- For Particle 2 (released at t=1):
- At time t, the time since its release is t−1. Thus, the distance fallen is:
H2=12g(t−1)2
- According to the problem, the distance between the two particles is 10 meters:
H1−H2=10
- Substituting the expressions for H1 and H2:
12gt2−12g(t−1)2=10
- Factor out 12g:
12g(t2−(t−1)2)=10
- Expanding (t−1)2:
(t−1)2=t2−2t+1
- Therefore:
t2−(t2−2t+1)=2t−1
- Substituting back:
12g(2t−1)=10
- Plugging in the value of g:
12×10(2t−1)=10
- Simplifying:
5(2t−1)=10
- Dividing both sides by 5:
2t−1=2
- Solving for t:
2t=3⇒t=32=1.5seconds
The two particles will be 10 meters apart after 1.5 seconds from the release of the first particle.
Topper's Solved these Questions
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:MCQ_TYPE
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:COMPREHENSION_TYPE
Explore 19 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 11 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
Similar Questions
Two diamonds begin a free fall from rest from the same height, 1.0 s apart. How long after the first diamond begins to fall will the two diamonds be 10 m apart? Take g=10m/s2.
View SolutionTwo balls are released from the same height at an interval of 2s. When will the separation between the balls be 20m after the first ball is released? Take g=10m/s2.
View Solution
Knowledge Check
Two particles are released from the same height at an interval of 1s. How long after the first particle begins to fall will the two particles be 10m apart? (g=10m/s2)
A1.5sB2sC1.25sD2.5sTwo bodies begin a free fall from rest from the same height 2 seconds apart. How long after the first body begins to fall, the two bodies will be 40 m apart? (Take g = 10ms−2)
A1 sB2 sC3 sD4 sTwo balls are dropped from the same point after an interval of 1s. If acceleration due to gravity is 10m/s2, what will be their separation 3 seconds after the release of first ball?
A5 mB10 mC25 mD30 m
Two particles begin to fall freely from the same height but the second falls t0 second after the first. Find the time (after the dropping of first) when separation between the particles is h0.
View SolutionA particle is thrown vertically up from the top of a building of height 20m with initial velocity u. A second particle is released from the same point 1 second later. If both particles reach the ground at the same instant ,3u=m/s. [Takeg=10m/s2]
View SolutionTwo equally charged particles, held 3.2×10−3m apart, are released from rest. The initial accelerartion of the first particle is observed to be 7.0m/s2 and that of the secound to be 9.0m/s2. If the mass of the first particle is 6.3×10−7kg, what are (a) the mass of the secound particle adn (b) teh magnitude of the charge of each particle ?
View SolutionTwo particles A and B masses 1 kg and 2 kg respectivelty are projected in the same vertical line as shown in figure with speeds uA=200m/s and uB=85m/s respectively. Initially they were 90 m apart. Find the maximum height attained by the centre of mass of the system of particles A and B, from the initial position of centre of mass of the system. Assume that none of these particles collides with the ground in that duration Take g=10m/s2
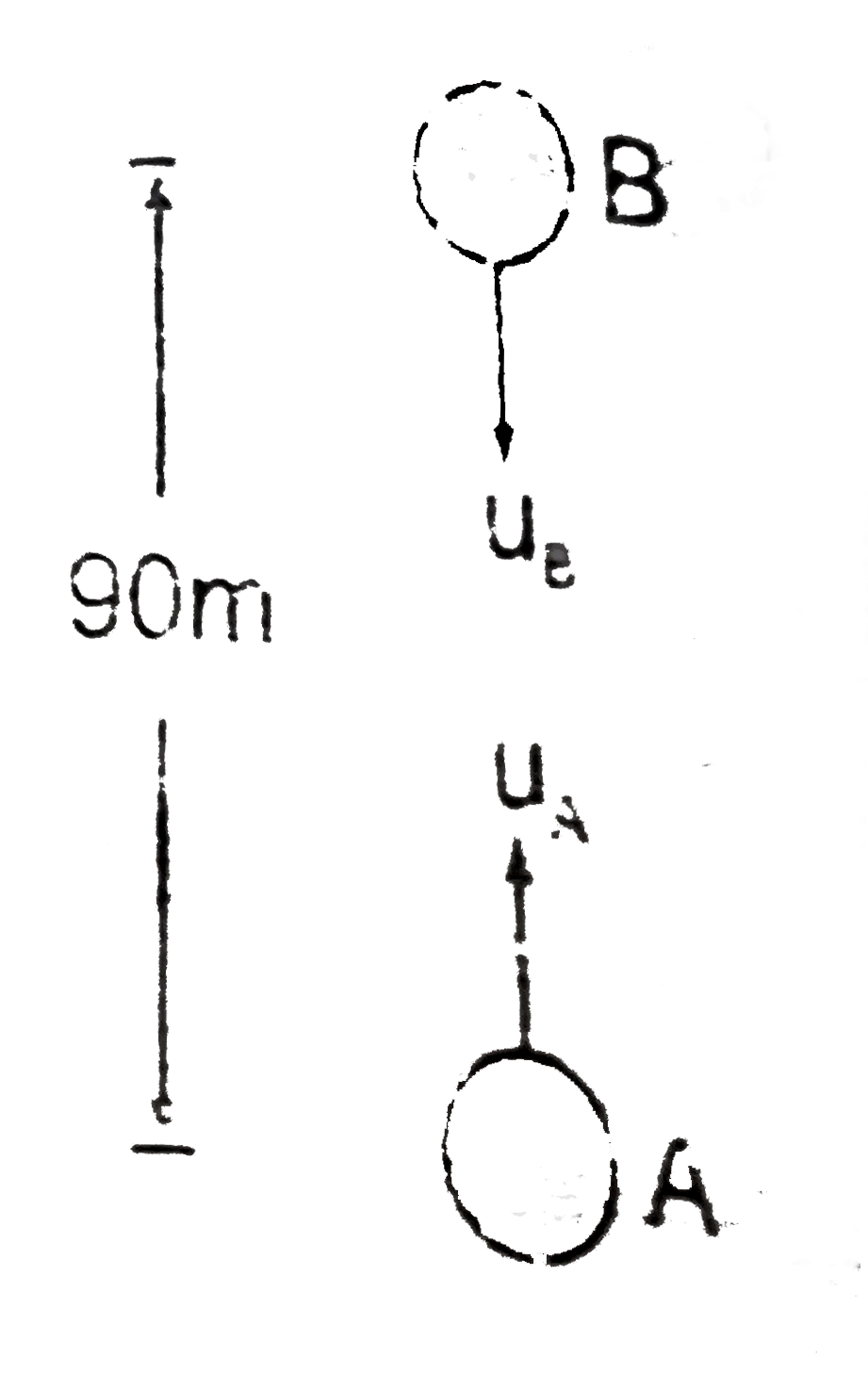
View SolutionTwo balls of equal masses are thrown upwards, along the same vertical direction at an interval of 2 seconds, with the same initial velocity of 40m/s. Then these collide at a height of (Take g=10m/s2).
View Solution

