A charged particle (q.m) released from origin with velocity v=v0ˆi in a uniform magnetic field B=B02ˆi+√3B02ˆJ.
Z-component of velocity is √3v02 after in t=……….
2πmB0q
πmB0q
πm2B0q
2πm4B0q
The correct Answer is:c
Step by step video, text & image solution for A charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ. Z-component of velocity is (sqrt3v_(0))/(2) after in t=………. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Matrix Matching type Questions
Explore 11 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Integer type Questions
Explore 10 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:More than One Option is Correct
Explore 25 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEYChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
Similar Questions
For the path of a charged particle math the following.

View SolutionTwo parallel, long wires carry currents t1andt2 with t1>t2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 μT. If the direction of i2 is reversed, the field becomes 30 μT. Find the ratio i1i2.
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process
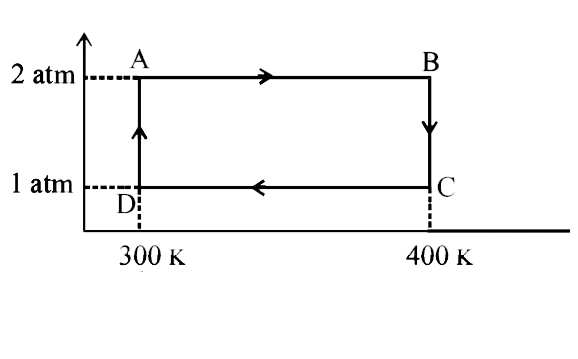
(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
View SolutionWrite down the number of significant figures in the following (a) 6428 (b)62.00 (c)0.00628 cm (d) 1200N
View SolutionA magnetic field vec(B)=-B_(0)hati exists within a sphere of radius R=v_(0)T sqrt(3) where T is the time period of one revolution of a charged particle starting its motion from origin and moving with a velocity vec(v)_(0)=(v_(0))/2sqrt(3)hati-(v_(0))/2 hatj . Find the number of turns that the particle will take to come out of the magnetic field.
View SolutionA particle of charge per unit mass α is released from origin with a velocity →v=v0ˆi in a magnetic field
→B=−B0ˆk for x≤√32v0B0α
and →B=0 for x>√32v0B0α
The x-coordinate of the particle at time t(π3B0α) would be
View SolutionA uniform electric field, underset(E)to=E_(0)hati and a uniform magnetic field, underset(B)to=B_(0)hati exist in region y gt 0. A particle hav- ing positive charge q and mass m is projected from the origin with a velocity underset(V)to=V_(0)hati+V_(0)hatJ. The velocity of the particle when it leaves the region of fields was found to be -underset(V)to. (i) Find the ratio (E_(0))/(B_(0)) in terms of v0. (ii) Find the co-ordinates of the point where the particle leaves the fields. (iii) Find the minimum speed of the particle during the course of the motion.
View SolutionIn the region between the plane z=0 and z=a (a gt 0) , the uniform electric and magnetic fields are given by vecE=E_(0)(hatk-hatj) , vecB=B_(0)hati . The region defined by a le z le b contains only magnetic field vecB= -B_(0)hati . Beyond z gt b no field exits. A positive point charge q is projected from the origin with velocity v_(0)hatk . Assuming the mass of the particle to be (2)/(3)(qE_(0)a)/(v_(0)^(2)) . The value of E_(0) such that the particle moves undeviated upto the plane z=a is
View SolutionIn the region between the plane z=0 and z=a (a gt 0) , the uniform electric and magnetic fields are given by vecE=E_(0)(hatk-hatj) , vecB=B_(0)hati . The region defined by a le z le b contains only magnetic field vecB= -B_(0)hati . Beyond z gt b no field exits. A positive point charge q is projected from the origin with velocity v_(0)hatk . Assuming the mass of the particle to be (2)/(3)(qE_(0)a)/(v_(0)^(2)) . The minimum value of b such that the particle reverses its direction completely is
View SolutionIn the region between the plane z=0 and z=a(a>0), the uniform electric and magnetic fields are given by →E=E0(ˆk−ˆj), →B=B0ˆi. The region defined by a≤z≤b contains only magnetic field →B=−B0ˆi. Beyond z>b no field exits. A positive point charge q is projected from the origin with velocity v0ˆk. Assuming the mass of the particle to be 23qE0av20.
When the particle just reverse its direction, all the fields are switched off. Time taken by the particle to touch the plane z=0 from that instant is
View SolutionA charged particle of specific charge (Charge/mass) alpha is released from origin at time t=0 with a velocity given as vecv=v_(0)(hati+hatj) The magnetic field in region is uniform with magnetic induction vecB=B_(0)hati . Coordinates of the particle at time t=(pi)/(B_(0)alpha) are:
View SolutionA charge praticule of sepeific charge (charge/ mass ) alpha is realsed from origin at time t=0 with velocity v= v_(0)(hati+hatj) in unifrom magnetic fields B= B_(0)hati . Co-ordinaties of the particle at time t = (pi)/(B_(0)alpha) are
View SolutionA charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ . Pitch of the helical path described by the particle is
View SolutionA charged particle (q.m) released from origin with velocity v=v_(0)hati in a uniform magnetic field B=(B_(0))/(2)hati+(sqrt3B_(0))/(2)hatJ . Maximum z-coordinate of the particle is
View Solution

