A portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
its Z co-ordinate can never be negative
its x co-ordinate can never be positive
its x and z co-ordinates cannot be zero at the same time
its y co-ordinate will be proportional to its time of flight
The correct Answer is:b,d
Step by step video, text & image solution for A portion is fired from origin with velocity vec(v) = v_(0) hat(j)+ v_(0) hat(k) in a uniform magnetic field vec(B) = B_(0) hat(j). In the subsequent motion of the proton by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Comprehension type Questions
Explore 16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Matrix Matching type Questions
Explore 11 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Only One Option is Correct
Explore 45 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEYChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
Similar Questions
A particle of specific charge 'α' is projected from origin at t=0 with a velocity →V=V0(ˆi−ˆk) in a magnetic field →B=−B0ˆk. Then : (Mass of particle =1 unit)
View SolutionA wire forming one cycle of sine curve is moved in x-y plane with velocity →V=Vxˆi+Vyˆj. There exist a magnetic field →B=−B0ˆk.
Find the motional emf decelop across the ends PQ of wire.
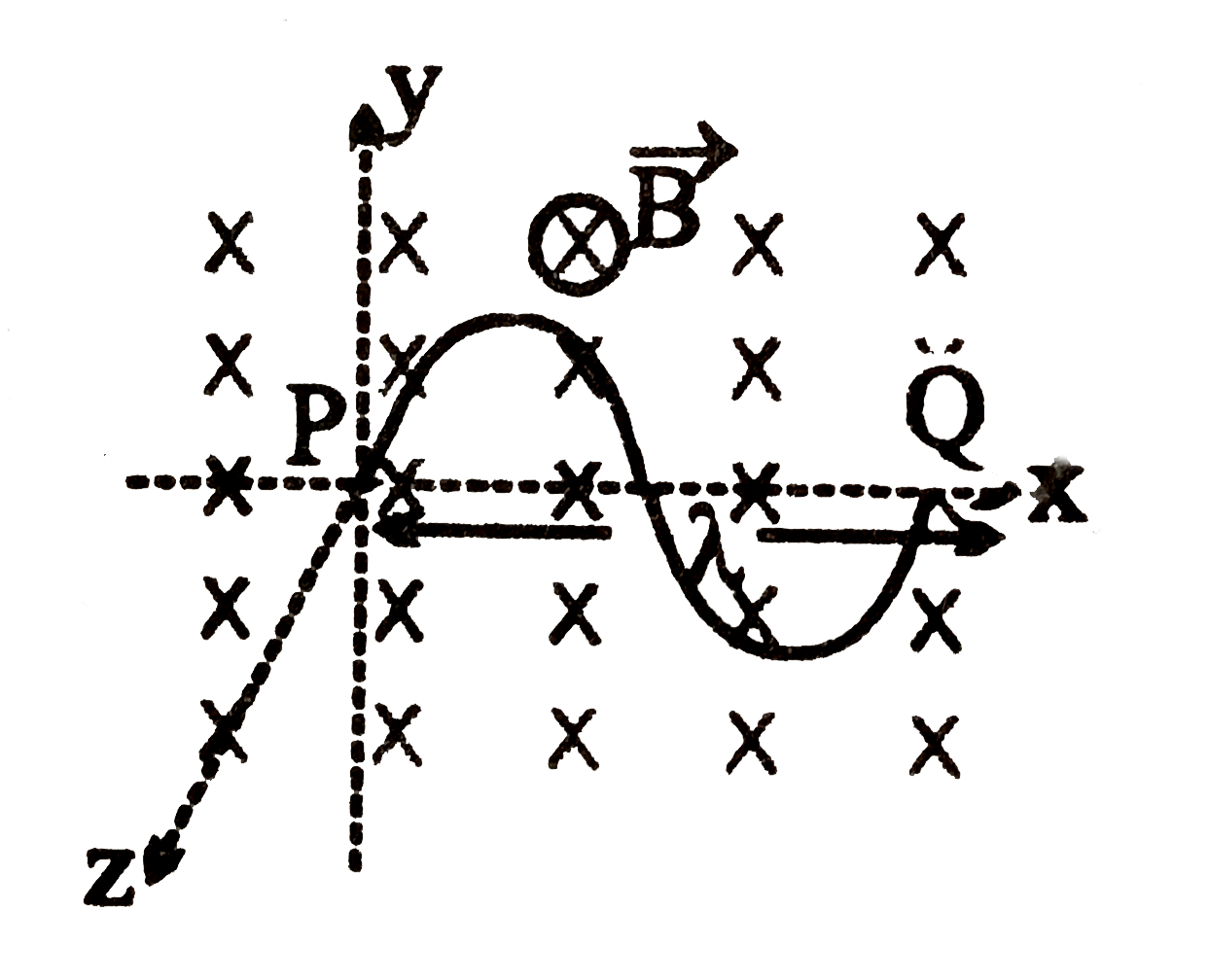
View Solution
Knowledge Check
In uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Angle between v and B isA45∘B30∘C60∘D120∘In uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Axis of helix is alongAX-axisBY-axisCNegative Y-axisDZ-axisIn uniform magnetic field, if angle between →vand→Bis0∘<0<90∘, the path of particle is helix. Let v1 be the component of →valong→Bandv2 be the component perpendicular to →B. Suppose p is the pitch. T is the time period and r is the radius of helix. Then
T=2πmqB,r=mv2qB,P=(v1)T
Assume a charged particle of charge q and mass m is released from the origin with velocity →v=v0ˆi−v0ˆk in a uniform magnetic field →B=−B0ˆk.
Pitch of helical path described by particle isA2mv0qB0B2πmv0qB0C√2πmv0qB0D√3πmv0qB0
An alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View SolutionA particle of charge q and mass m released from origin with velocity →v=v0ˆi into a region of uniform electric and magnetic fields parallel to y-axis. i.e., →E=E0ˆjand→B=B0ˆj. Find out the position of the particle as a functions of time
Strategy : Here →E∣∣→B
The electric field accelerates the particle in y-direction i.e., component of velocity goes on increasing with acceleration
ay=Fym=Fem=qE0m
The magnetic field rotates the particle in a circle in x-z plane (perpendicular to magnetic field) The resultant path of the particle is a helix with increasing pitch.
Velocity of the particle at time t would be
→v(t)=vxˆi+vyˆj+vzˆk
View SolutionA charged particle of specific charge (charge/mass) α released from origin at time t=0 with velocity →v=v0(ˆi+ˆj) in uniform magnetic field →B=B0ˆi. Coordinates of the particle at time t=π/(B0α) are
View SolutionA conductor AB of length l moves in xy plane with velocity →v=v0(ˆi−ˆj). A magnetic field →B=B0(ˆi+ˆj) exists in the region. The induced emf is
View SolutionA magnetic field →B=B0ˆj , exists in the region a<x<2a , and vec(B) = -B_(0) hat(j),∈theregion2a lt xlt 3a,whereB_(0)isapositiveconstant.Apositivep∮char≥mov∈gwithavelocityvec(v) = v_(0) hat (i),wherev_(0) is a positive constant , enters the magnetic field at x=a . The trajectory of the charge in this region can be like

View Solution

