Two identical particles having the same mass m and charges +q and -q separated by a distance d enter a uniform magnetic field B directed perpendicular to paper inwards with speeds v1andv2 as shown in Fig. 1.139. The particles will not collide if

d>mBq(V1−V2)
d<mBq(V1−V2)
d>2mBq(V1−V2)
V1=V2
The correct Answer is:C
Step by step video, text & image solution for Two identical particles having the same mass m and charges +q and -q separated by a distance d enter a uniform magnetic field B directed perpendicular to paper inwards with speeds v_1 and v_2 as shown in Fig. 1.139. The particles will not collide if by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEYCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
Two particles having identical masses and charges 2Q and Q are moving with velocities v and 2v resp. In uniform magnetic field B. Find ratio of radius of circle described by them
View SolutionA positive charge particle enters and comes out (at 60∘ and 37∘ as shown) from a uniform magnetic field which is perpendicular to paper inwards in a finite space of width 60 cm as shown in the figure. Find the radius of curvature of the charged particle (in meter) when it is inside the magnetic field.

View Solution
Knowledge Check
A n electrically charged particle enters into a uniform magnetic induction field in a direction perpendicular to the field with a velocity v then it travels
Aina straight line without accelerationBwith force in the direction of the fieldCin a circular path with a radius directly proportional toDin a circular path with a radius directly proportional to its velocityA charged particle of mass m and charge q is accelerated through a potential differences of V volts. It enters of uniform magnetic field B which is directed perpendicular to the direction of motion of the particle. The particle will move on a circular path of radius
A(√Vm2qB2)B2VmqB2C√2Vmq(1B)D√Vmq(qB)A V-shaped conducting wire is moved inside a magnetic field as shown in figure. Magnetic fiel d is perpendicular to paper inwards. Then
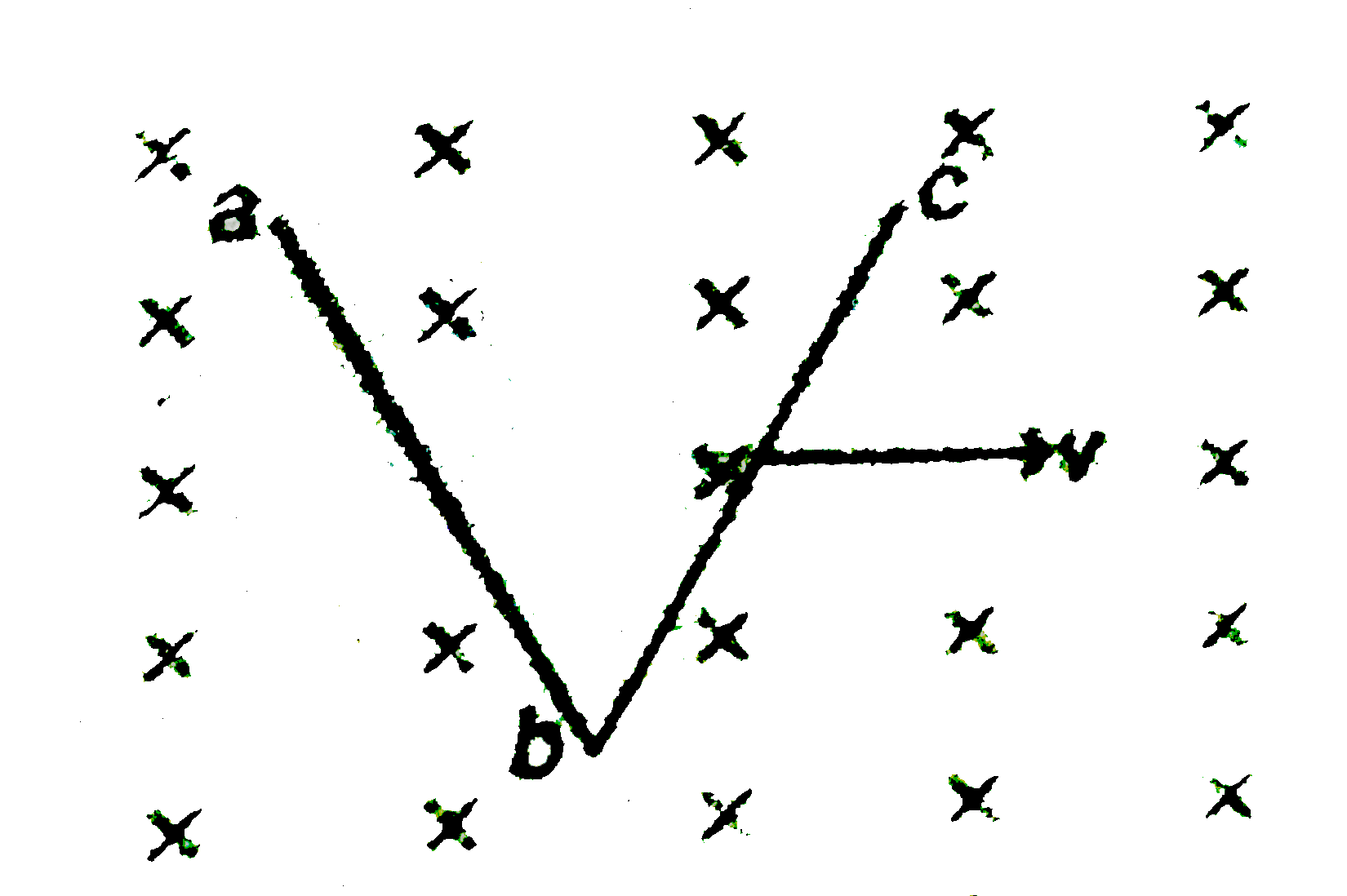 AVa=VcBVa>VcCVa>VbDVc>Vb
AVa=VcBVa>VcCVa>VbDVc>Vb
A charged particle of mass m and charge q is accelerated through a potential difference of V volts. It enters a region of uniform magnetic field which is directed perpendicular to the direction of motion of the particle. Find the radius of circular path moved by the particle in magnetic field.
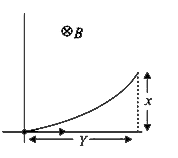
View SolutionA positively charged particle of charge 'q' enters in a uniform magnetic field B directed inward and is deflected a distance x after travelling a distance Y as shown in the figure. The magnitude of linear momentum of the particle is:
View SolutionA particle of charge -q and mass m enters a uniform magnetic field →B (perpendicular to paper inward) at P with a velocity v0 at an angle α and leaves the field at Q with velocity v at angle β as shown in fig.

View SolutionA particle of charge q and mass m is projected with a velocity v0 toward a circular region having uniform magnetic field B perpendicular and into the plane of paper from point P as shown in Fig. 1.136. R is the radius and O is the center of the circular region. If the line OP makes an angle θ with the direction of v0 then the value of v0 so that particle passes through O is

View SolutionA particule having charge q enters a rection of untiormal magnetic field B (direction inwards) and in denfectro as shown . The magnetic of the momentum of the particles is
View Solution
