Two identical thin planoconvex lenses of refractive index n are silvered, one on the plane side and other on the convex side. The ratio of their for lengths is
n/(n−1)
(n−1)/n
(n+1)/n
n
The correct Answer is:A
Step by step video, text & image solution for Two identical thin planoconvex lenses of refractive index n are silvered, one on the plane side and other on the convex side. The ratio of their for lengths is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:B. More than one option is correct
Explore 20 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:C. comprehension type question
Explore 14 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Integer type q.
Explore 15 Videos
- PROPERTIES OF MATTERBook:DC PANDEYChapter:PROPERTIES OF MATTERExercise:Integer
Explore 8 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
Similar Questions
Two identical equiconvex lenses of refractive index 3/2 and focal length 16 cm are kept in contact. The space between the lenses is filled with water of refractive index 4/3. What is the focal length of the combination ?
View SolutionThe figure below shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. Another thin lens of refractive index μ3 has same radius of curvature R on the two surface between the plano-convex and plano-concae lenses that the plane surfaces are parallel to each other. Find the focal length of the combination.
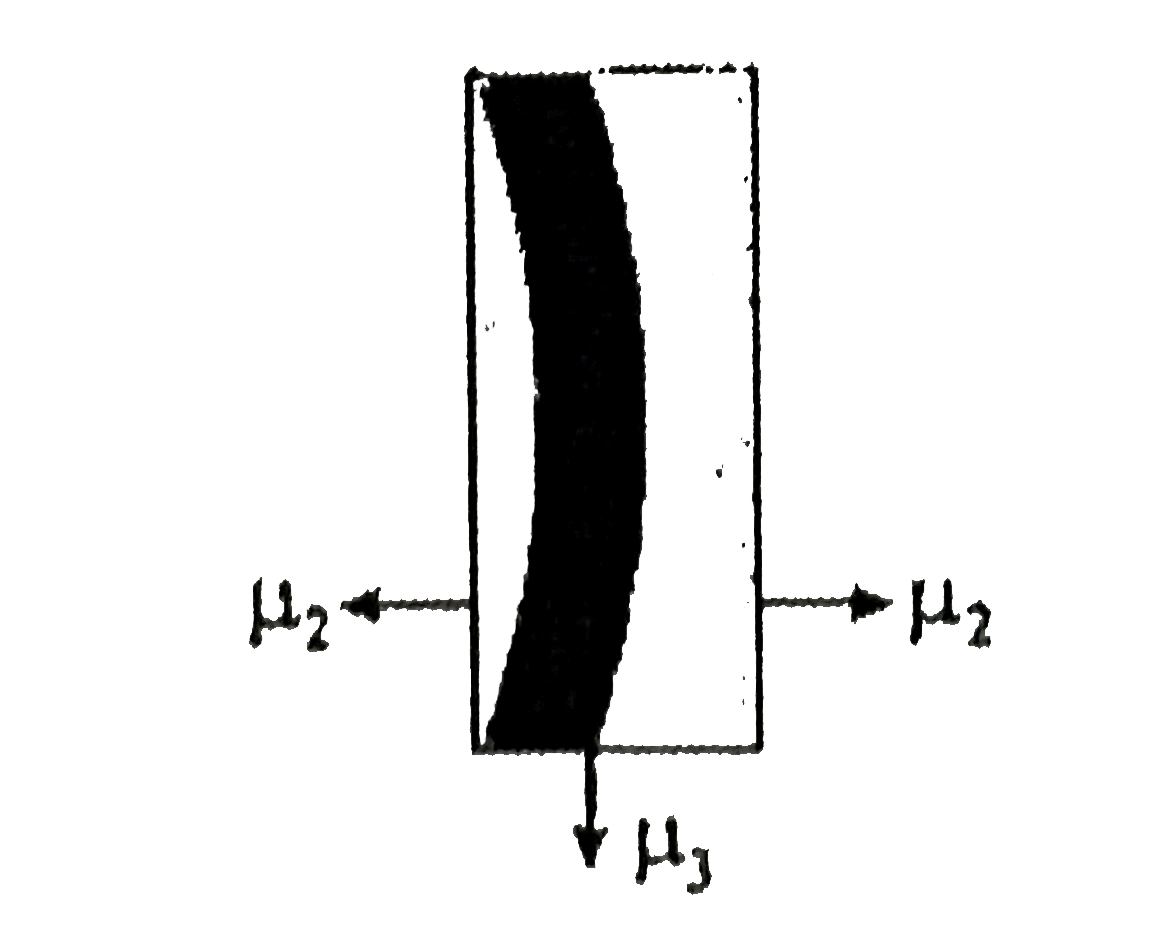
View Solution
Knowledge Check
Two identical thin planoconvex glass lenses (refractive index 1.5) each having radius of curvature of 20cm are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
A−20cmB−25cmC−50cmD50cmChoose the most appropriate option.
Two identical thin plano-convex glass lenses (refractive index 1.5) each having radius of curvature of 20 cm are placed with their convex surfaces in contact at the center. The intervening space is lled with oil of refractive index 1.7. The focal length of the combination is:A−20cmB−25cmC−50cmD50 cmTwo identical thin planoconvex glass lenses (refractive index 1.5) each having radius of curvature of 20cm are placed with their convex surfaces in contact at the centre. The intervening space is filled with oil of refractive index 1.7. The focal length of the combination is
A−20cmsB−25cmC−50cmD50cm
The adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionA liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangement P and Q are shown in figure-. The system is:

View SolutionTwo similar planoconvex lenses are combined together in three different ways as shown in the adjoining figure. The ratio of the focal lengths in three cases will be

View SolutionA convex lens has its radi of curvature equal. The focal length of the lens is f. It is is dividded vertically into two identical plano-convex lenses by cutting it, then the focal length of the plane -convex lens is (μ= the refractive index of the material of the lens)
View SolutionA liquid of refractive index 1.33 is placed between two identical plano-convex lenses, with refractive index 1.50. Two possible arrangement P and Q are shown. The system is
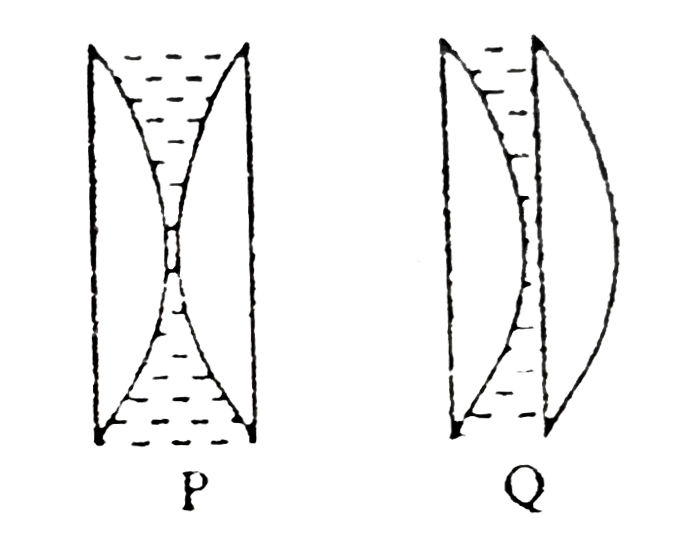
View Solution

