If k is a positive constant such that 0<k<1, which of the following could be the graph of y−x=k(x+y) ?
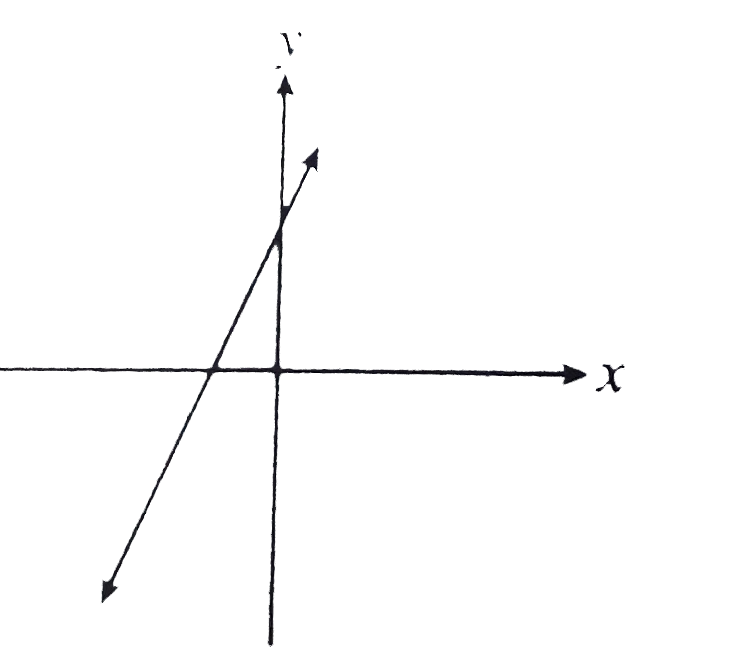

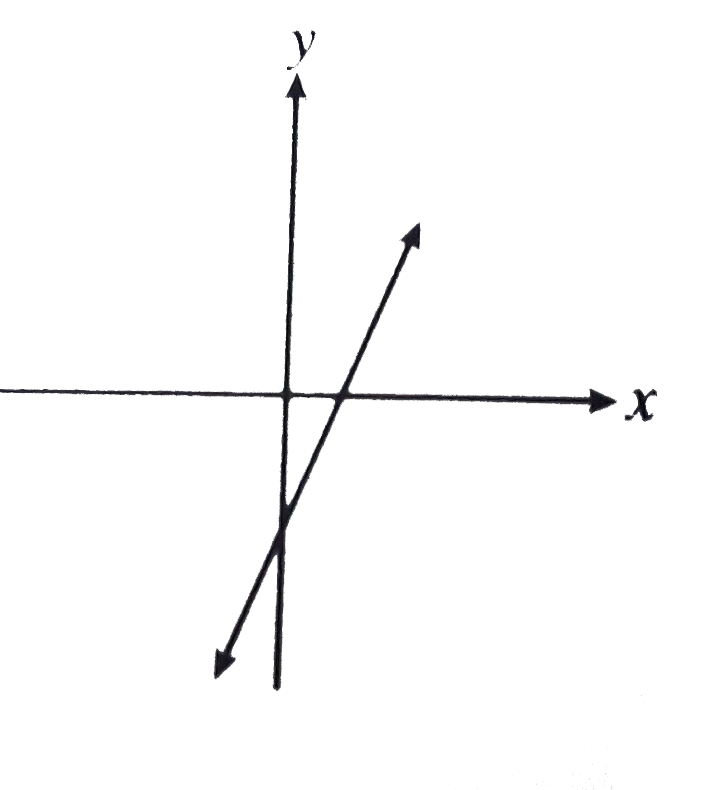

The correct Answer is:B
To solve the equation y−x=k(x+y) where k is a positive constant such that 0<k<1, we will follow these steps:
Step 1: Rearranging the Equation
Start with the given equation:
y−x=k(x+y)
We can rearrange this to isolate y:
y−ky=kx+x
This simplifies to:
y(1−k)=(k+1)x
Step 2: Solving for y
Now, divide both sides by (1−k) (since k<1, 1−k>0):
y=(k+1)(1−k)x
Step 3: Analyzing the Slope
The slope of the line is given by:
slope=(k+1)(1−k)
Since k is a positive constant less than 1, both k+1 and 1−k are positive. Therefore, the slope is positive.
Step 4: Finding the y-intercept
Since the equation is in the form y=mx+b (where b is the y-intercept), and there is no constant term added to y, we can conclude that the line passes through the origin (0,0).
Step 5: Conclusion
Since the slope is positive and the line passes through the origin, the graph of the equation y−x=k(x+y) will be a straight line through the origin with a positive slope.
Now, we can eliminate options that do not fit this description:
- Any option with a y-intercept (not passing through the origin) can be eliminated.
- Any option with a negative slope can also be eliminated.
Thus, the correct graph would be the one that shows a straight line through the origin with a positive slope.
Start with the given equation:
y−x=k(x+y)
We can rearrange this to isolate y:
y−ky=kx+x
This simplifies to:
y(1−k)=(k+1)x
Now, divide both sides by (1−k) (since k<1, 1−k>0):
y=(k+1)(1−k)x
The slope of the line is given by:
slope=(k+1)(1−k)
Since k is a positive constant less than 1, both k+1 and 1−k are positive. Therefore, the slope is positive.
Since the equation is in the form y=mx+b (where b is the y-intercept), and there is no constant term added to y, we can conclude that the line passes through the origin (0,0).
Since the slope is positive and the line passes through the origin, the graph of the equation y−x=k(x+y) will be a straight line through the origin with a positive slope.
- Any option with a y-intercept (not passing through the origin) can be eliminated.
- Any option with a negative slope can also be eliminated.
Topper's Solved these Questions
Similar Questions
If 12x=k is the directrix of parabola y2+4y+3x=0, then which of the following true? (A) k=25 (B) k=0 (C) k=5 (D) k=15
View SolutionQuestion 1 and 2 refer to the information and graph below.
Let function f be defined by the graph in the accompanying figure.
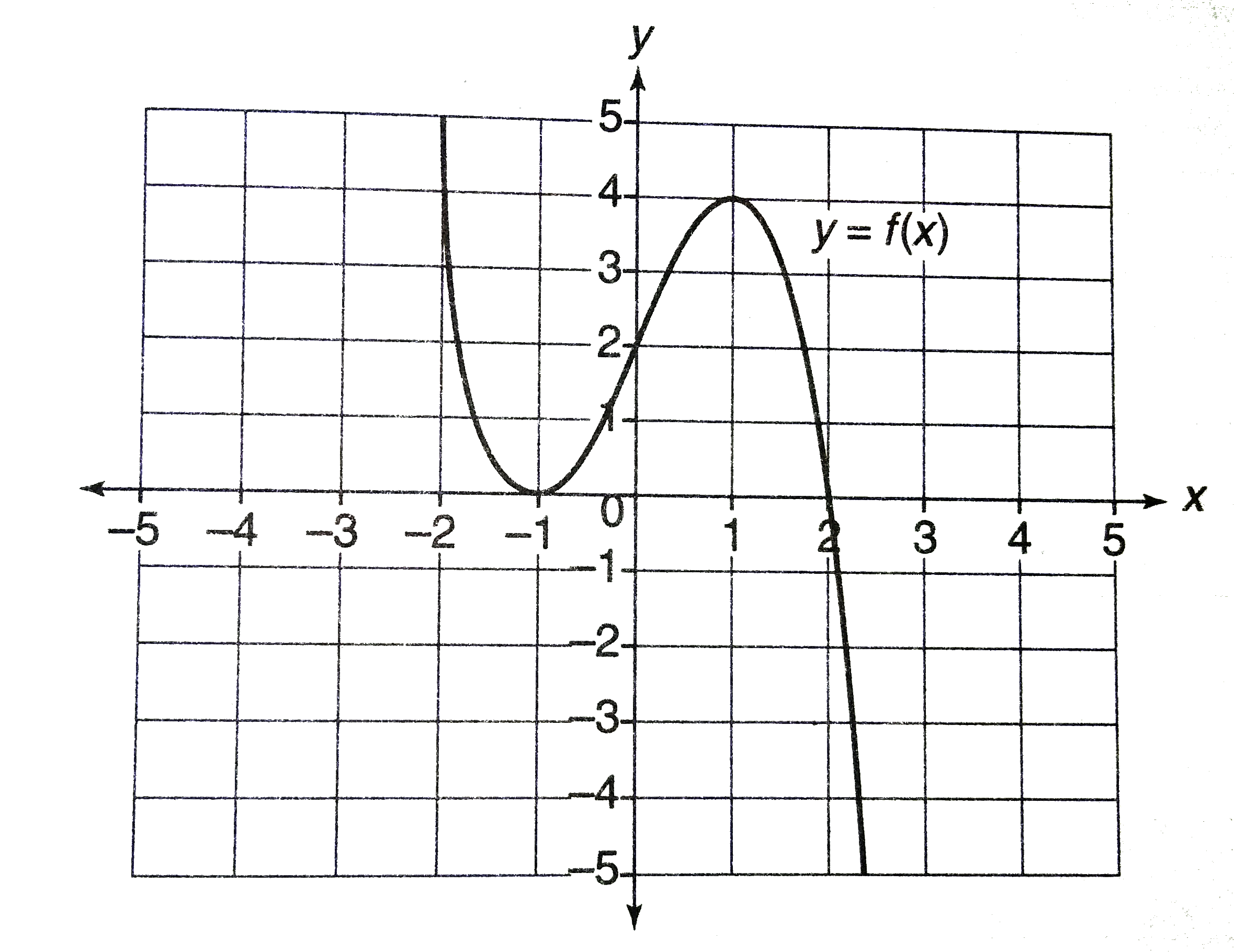
Q. For what positive integer k is (1, 0) an x-intercept of the graph of y=f(x−k)?
View Solution
Knowledge Check
Which of the following could be the graph of 2x+3y+12=0 ?
A B
B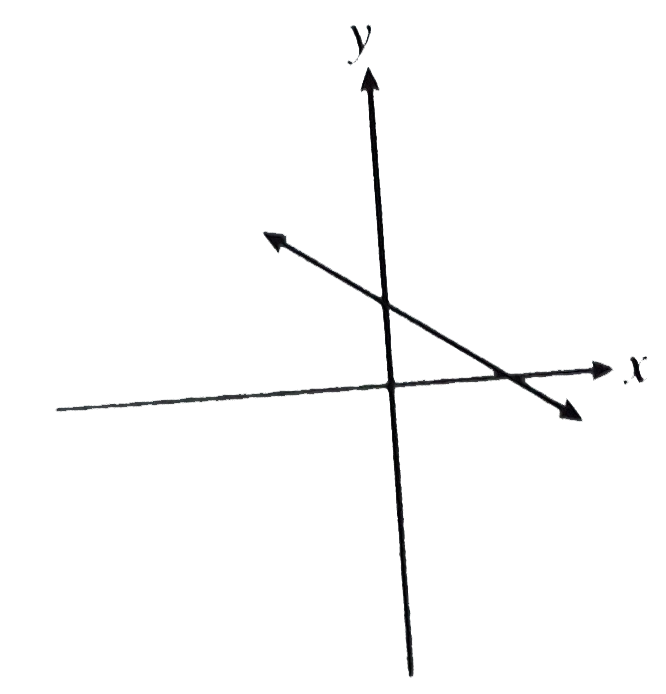 C
C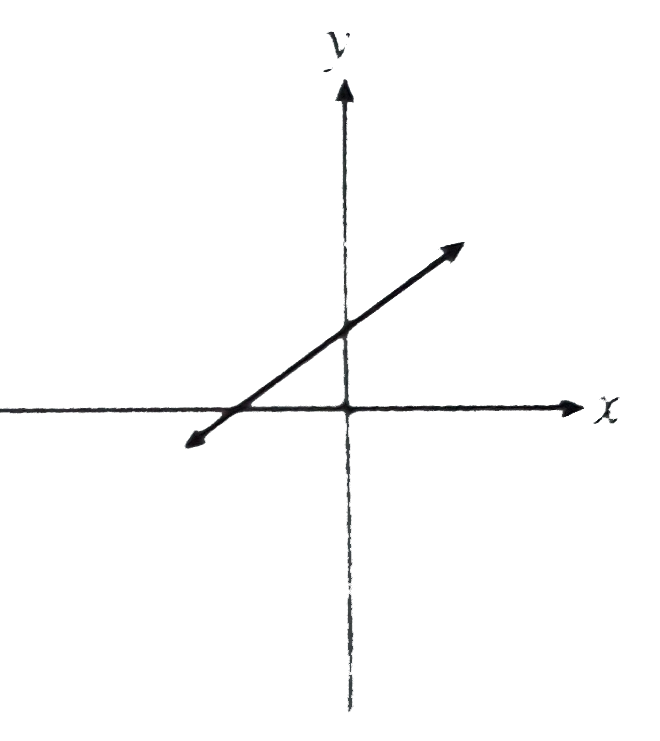 D
D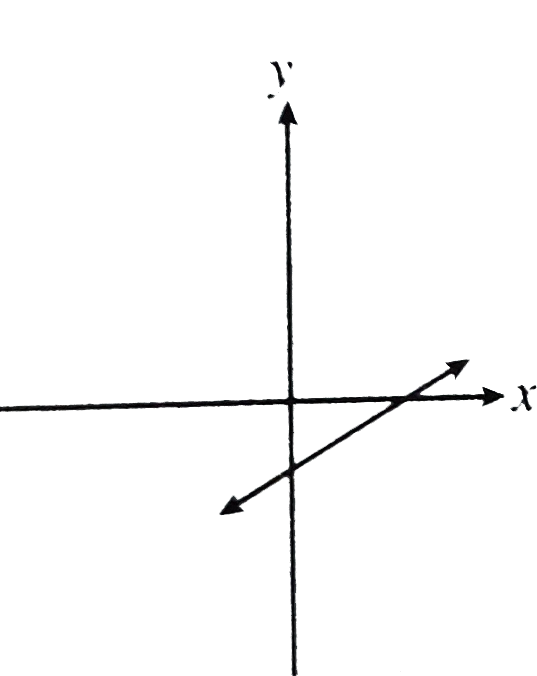
f (x) = (x + 3)(x − k)
T he function f is defined above. If k is a positive integer, which of the following could represent the graph of y = f (x) in the xy-plane?A B
B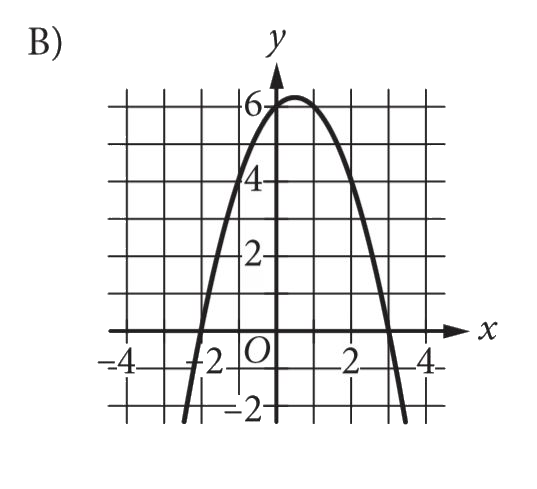 C
C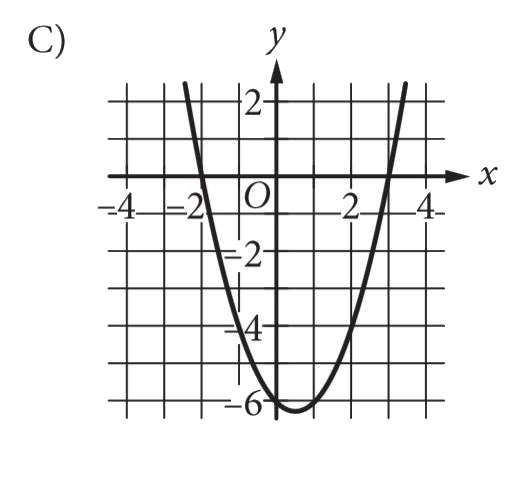 D
D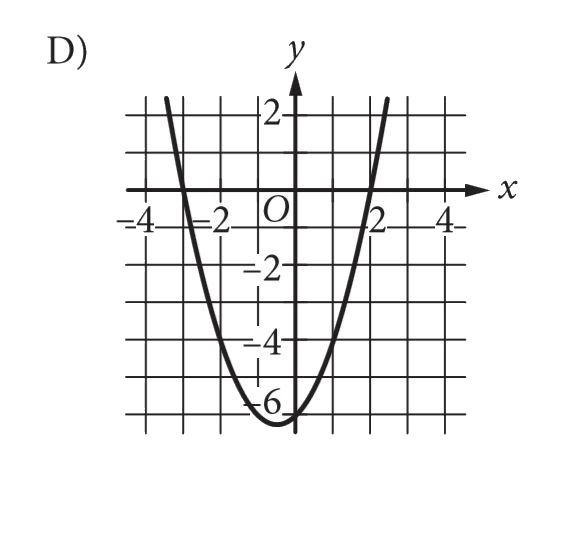
The graph of y=f(x) is shown below.
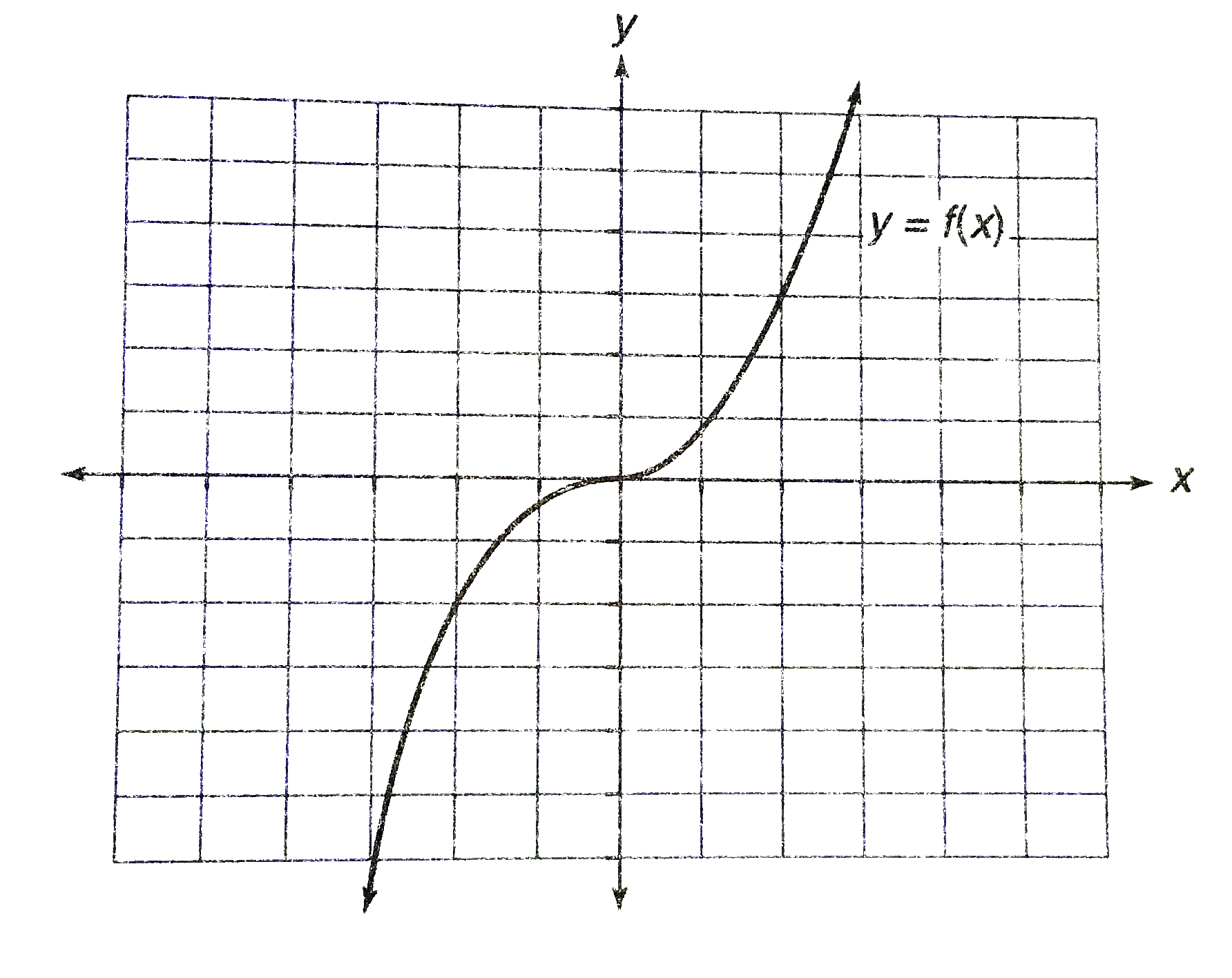
Which of the following could represents the graph of y=f(x−2)+1?A B
B C
C D
D
If is given that cosx=k, where x is the radian measure of an angle and π<x<3π2. If cosz=−k, which of the following could not–––– be the value of z ?
View Solution
If g(x)=−2 intersects the graph of y=f(x)+k at one point, which of these choices could be the value of k?
View SolutionIf kgt4 is a constant, how would you translate the graph of y=x2 to get the graph of y=x2+4x+k?
View SolutionWhich could be the graph of y=x2+3x+k , where k is an integer ?
View SolutionThe graph of x=−y2+2 and the graph of the line k intersect at (0,p) and (1,q). Which one of the following is the smallest possible slope of line k?
View Solution

