When the current through a solenoid increases at a constant rate, the induced current in the solenoid
Is constant and is in the direction of the increasing current in it
Is a constant and is opposite to the direction of the increasing current in it.
Increases with time and is in the direction of increasing current in it.
Increases with time and is opposite to the direction of the increasing current in it
The correct Answer is:B
To solve the question regarding the behavior of induced current in a solenoid when the current through it increases at a constant rate, we can follow these steps:
1. Understanding the Scenario:
- We have a solenoid through which the current is increasing at a constant rate. This means that the rate of change of current (di/dt) is constant.
2. Applying Lenz's Law:
- According to Lenz's Law, the direction of the induced current is such that it opposes the change in magnetic flux that produced it. The induced electromotive force (EMF) can be expressed as:
EMF=−Ldidt
- Here, L is the inductance of the solenoid, and didt is the rate of change of current.
3. Analyzing the Induced EMF:
- Since the current is increasing at a constant rate, didt is a constant value. Therefore, the induced EMF will also be constant in magnitude.
- The negative sign indicates that the induced EMF (and hence the induced current) will flow in a direction that opposes the increase in current through the solenoid.
4. Conclusion about Induced Current:
- The induced current in the solenoid will be constant in magnitude and will flow in the opposite direction to the increasing current.
5. Final Answer:
- The induced current in the solenoid is constant and flows in the opposite direction to the increasing current.
- We have a solenoid through which the current is increasing at a constant rate. This means that the rate of change of current (di/dt) is constant.
- According to Lenz's Law, the direction of the induced current is such that it opposes the change in magnetic flux that produced it. The induced electromotive force (EMF) can be expressed as:
EMF=−Ldidt
- Here, L is the inductance of the solenoid, and didt is the rate of change of current.
- Since the current is increasing at a constant rate, didt is a constant value. Therefore, the induced EMF will also be constant in magnitude.
- The negative sign indicates that the induced EMF (and hence the induced current) will flow in a direction that opposes the increase in current through the solenoid.
- The induced current in the solenoid will be constant in magnitude and will flow in the opposite direction to the increasing current.
- The induced current in the solenoid is constant and flows in the opposite direction to the increasing current.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Numerical MCQs
60 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Discussion Question-
21 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
389 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
Similar Questions
A long solenoid of diameter 0.1 m has 2×104 turns per meter. At centre of the solenoid is 100 turns coil of radius 0.01 m placed with its axis coinciding with solenoid axis. The current in the solenoid is decreased at a constant rate form + 2 A to - 2 A in 0.05 s. Find the e.m.f. induced in the coil. Also, find the total charge flowing through the coil during this time, when the resistance of the coil is 10π2ohm.
View SolutionA solenoid with N loops of wire tightly wrapped around an iron-core is carrying an electric current I. If the current through this solenoid is reduced to half, then what change would you expect in inductance L of the solenoid.
View Solution
Knowledge Check
A technician wraps wire around a tube of length 4π2 cm having a diameter of 8.00cm. When the windings are evenly spread over the full length of the tube, the result is a solenoid containing 1000turns of wire. If the current in this solonoid increases at the rate of 4.00A/s
the self-induced emf in the solenoid isA32mVB16mVC64mVD24mVA ring of area A and resistance R is placed on the axis of a solenoid. The mutual inductance between them is M. When the current in the solenoid changes at the rate of I, the magnetic moment of the ring is
AARMIBAI/RMCMRI/ADAMI/RThe flux linked with a coil is 0.8Wb when a 2 A current is flowing through it. If this current begins to increases at the rate of 400A/s, the induced emf in the coil will be
A20VB40VC80VD160V
A Current I0=1.9A flows in a long closed solenoid. The wire it is wound of is a superconducting state. Find the current flowing in the solenoid when the length of the solenoid is increased by η=5%.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
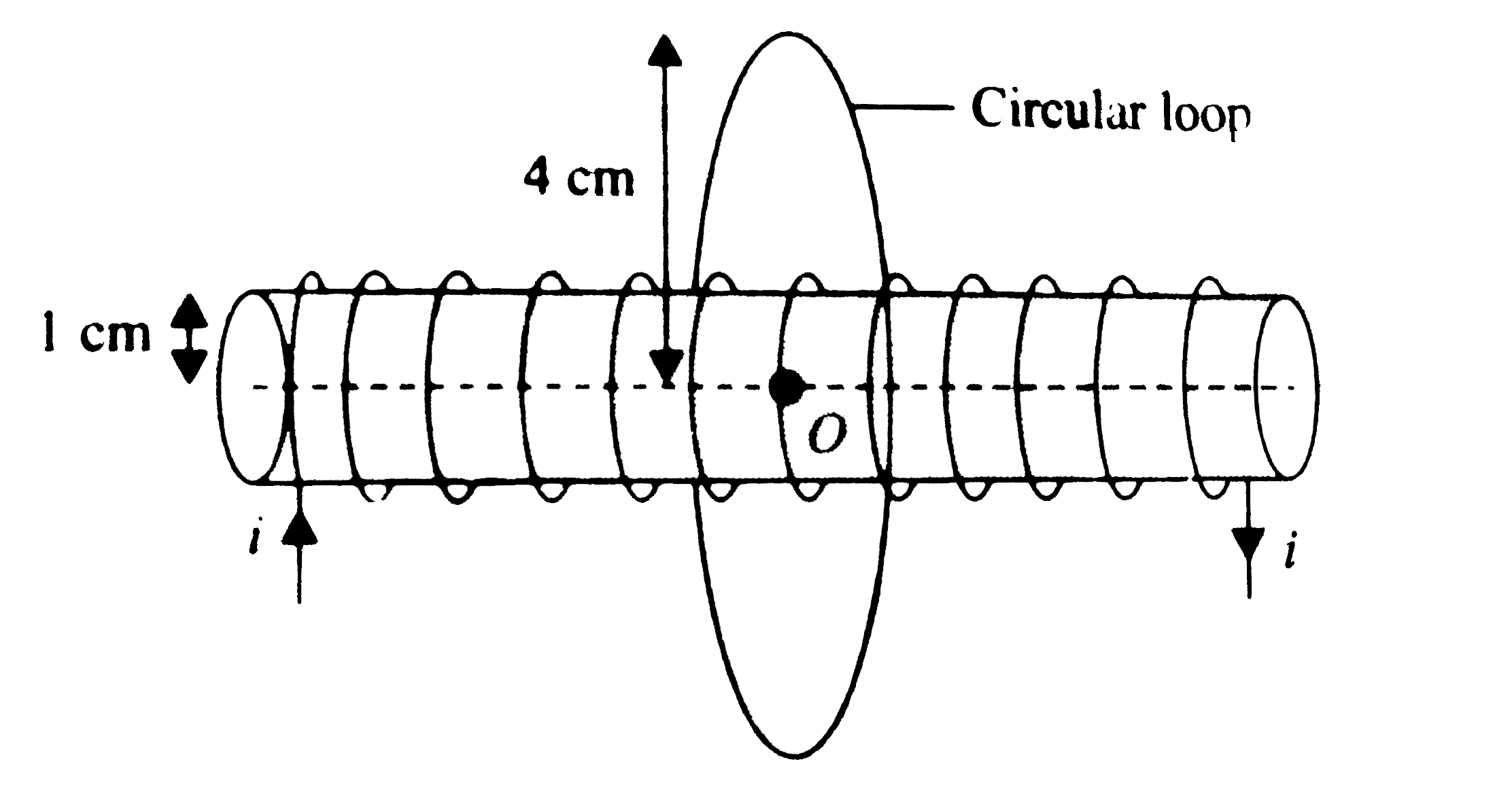
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionA small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is
View SolutionA long solenoid of radius 2R contains another coaxial solenoid of radius R. The coils have the same number of turns per unit length and initially both carry zero current. At time, t=0, current start increasing linearly with time in both solenoids. At any moment the current flowing in the inner coil is twice as large as that in the outer one and their directions are same. A charged particle, initially at rest between the two solenoids, start moving along a circular trajectory due to increasing current in the solenoid as shown in the figure What is the radius of the circle ? (Assume magnetic field due to each solenoid remains uniform over its cross-section.)

View SolutionAssertion (A) : Electromagnets are made of soft iron.
Reason (R) : The strenght of an electromagnet is increased by increasing the current flowing through the solenoid coil.
View Solution
