Two chunks of metal with heat capacities C1 and C2, are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t=0 the temperature difference betwene the two chunks of metal equals (ΔT)0. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time.
The correct Answer is:λSl
Step by step video, text & image solution for Two chunks of metal with heat capacities C_(1) and C_(2), are interconnected by a rod length l and cross-sectional area S and fairly low heat conductivity K. The whole system is thermally insulated from the environment. At a moment t = 0 the temperature difference betwene the two chunks of metal equals (DeltaT)_(0). Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chucks as a function of time. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the fisrt body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
Knowledge Check
Two rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
A(5/6)KB1.5KC1.2KD(8/9)KA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLTwo adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
AmsLAδtBemsLAδtCmsL2eAδtDmsL2Aδt
Two bodies each of mass m, having specific heats s, are connected by ametal rod of negligible heat capacity of length l, area of cross section A and thermal conductivity k. Initially both bodies are at different temperatures, find the time taken for the temperature difference between the two bodies to become half of the. initial value.
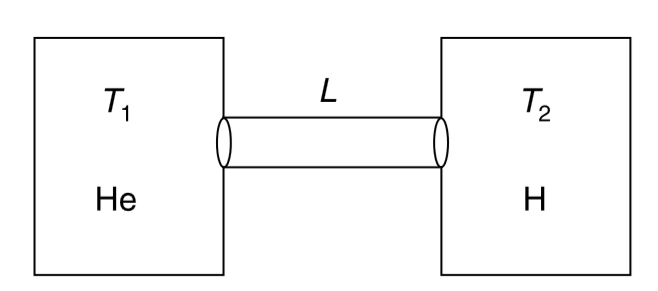
View SolutionTwo identical adiabatic containers of negligible heat capacity are connected by conducting rod of length L and cross sectional area A. Thermal conductivity of the rod is k and its curved cylindrical surface is well insulated from the surrounding. Heat capacity of the rod is also negligible. One container is filled with n moles of helium at temperature T1 and the other one is filled with equal number of moles of hydrogen at temperature T2(<T1). Calculate the time after which the temperature difference between two gases will becomes half the initial difference.
View SolutionA metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionTwo identical rods of length (L), area of cross-sectional (A) and thermal conductivity k are joined end to end. If temperature difference of free ends is ΔT, the heat Q0 flows along rods per second. Find the total heat flowing per second along the rods if the two rods are placed parallel and temperature difference of free ends is ΔT. There is no heat loss from curved surface.
View Solution
