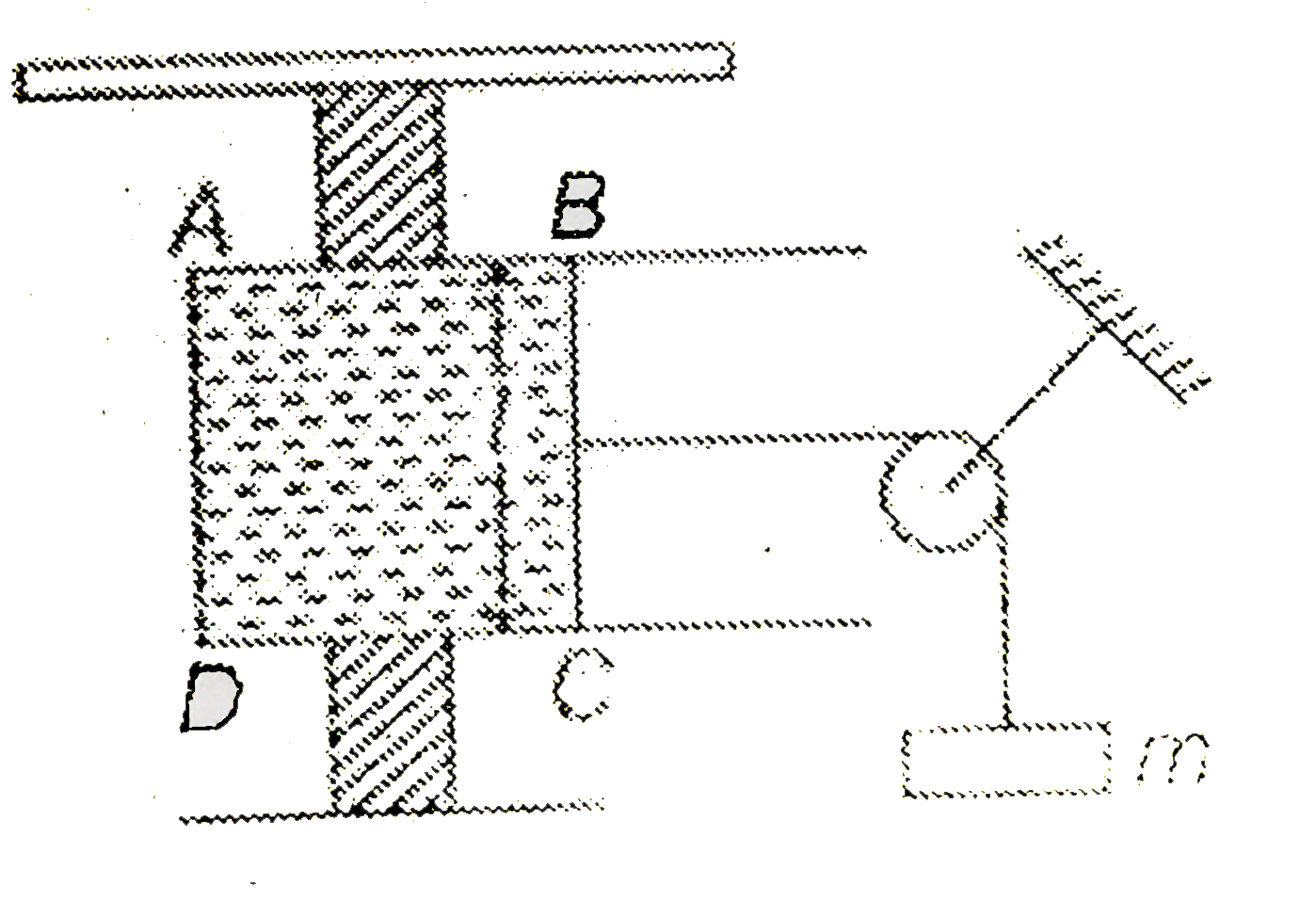
A wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
The correct Answer is:A
Step by step video, text & image solution for A wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
Similar Questions
A soap film is formed on a rectangular frame of length 7 cm dipping in soap solution. The frame hanges from the arm of a balance. An extra weight of 0.38 g is to be placed in the opposite pan to balance the pull on the frame. Calculate the surface tension of the soap solution. Giveng=980cms−2.
View SolutionA wire ring of 3cm redius is rested on the surface of a liquid and then reaised. The pull required is 3.03g more before the film breaks than it is afterwards. Find the surface tension of the liquid.
View Solution
Knowledge Check
A square wire frame of length l is dipped in a solution. When the frame is taken out, a liquid film is formed. What is the algebraic sum of all the force acting on the frame due to surface tension of the liquid? (givenσ=surface tension of the liquid).
A4σlB8σlC10σlD12σl
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod isA2π√lgB2π√lcosθgC2π√lgcosθD2π√lgtanθA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
 Ag2B(√3g)(2)Cg√2Dg
Ag2B(√3g)(2)Cg√2Dg
A soap film is formed on a rectangular frame of 7 cm side dipping into a scop solution. The frame hangs from the arm of a balance. An extra weight of 0.4 gram is to be placed in the opposite pan to balance the pull on the frame. Caluclate the surface tension of the soap solution.
View SolutionA liquid film is formed over a frame ABCD as shown in figure. Wire CD can slide without friction. The mass to be hung from CD to keep it in equilibrium is

View SolutionU - shaped film of a liquid is formed between a wire frame and movable wire 5 cm long. Then the force required to hold the wire in equilibrium is ,
(Surface tension of liquid is 0.024 N/m )
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.

View SolutionConsider a U-shaped frame with a sliding wire of length l and mass 'm' on its arm. It is dipped in a soap solution, taken out and placed in vertical position as shown in figure. Choose minimum value of m so that does not descent (Surface tension of soap solution is S)

View Solution
