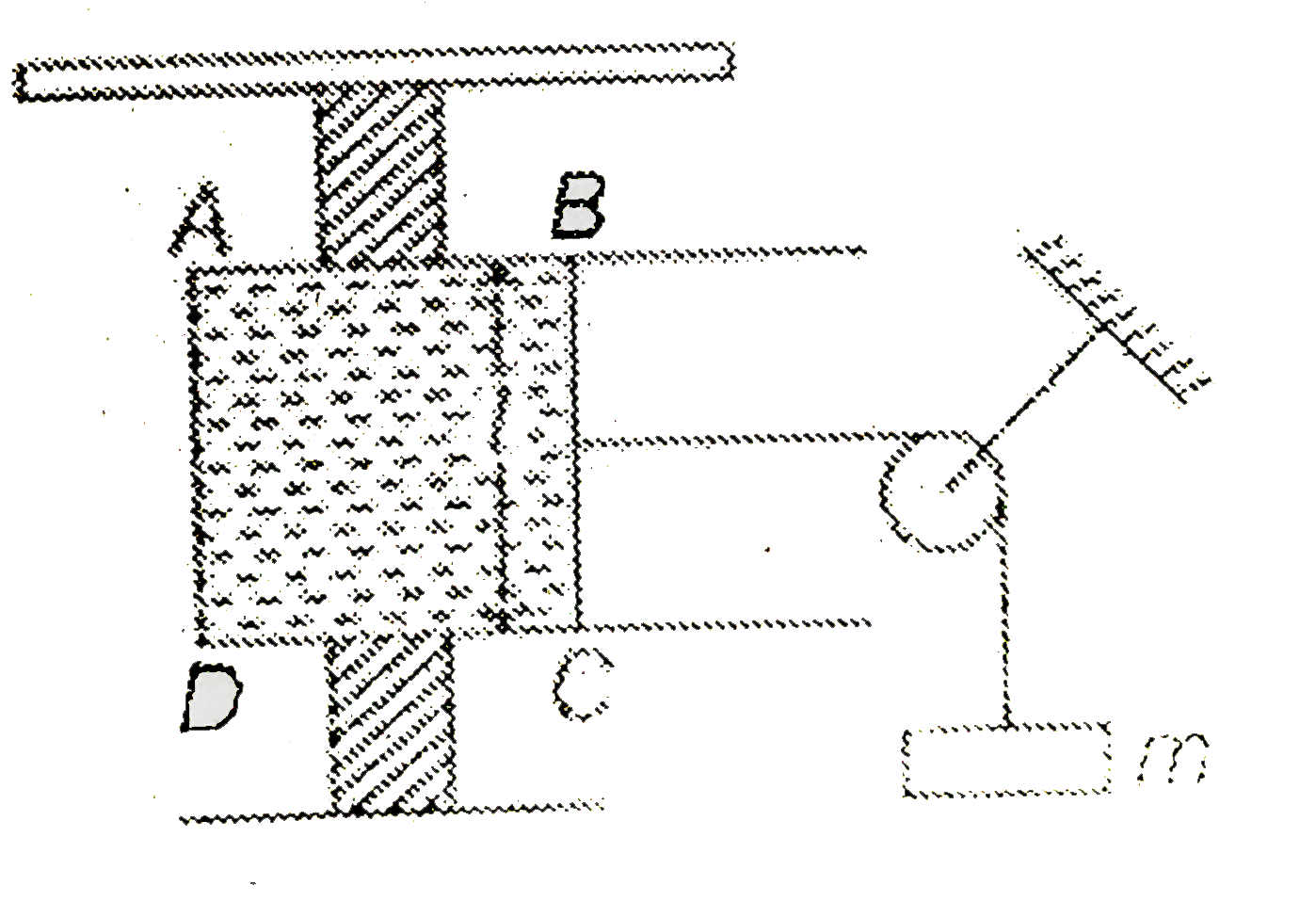
Consider a U-shaped frame with a sliding wire of length l and mass 'm' on its arm. It is dipped in a soap solution, taken out and placed in vertical position as shown in figure. Choose minimum value of m so that does not descent (Surface tension of soap solution is S)

2Slg
Slg
Sl2g
Sl4g
The correct Answer is:D
For wire to be in equilibrium,
mg=2Sl⇒m=2Slg
For mass less than 2Slg it will move upward So amongst the options Sl4g is the minimum mass.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.70
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.71
Explore 10 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.68
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
A rectangular wire frame of size 2 cm × 2 cm, is dipped in a soap solution and taken out. A soap film is formed, it the size of the film is changed to 3 cm x 3 cm, Calculate the work done in the process. The surface tension of soap film is 3×10−2 N/m.
View SolutionA soap film is formed on a rectangular frame of length 7 cm dipping in soap solution. The frame hanges from the arm of a balance. An extra weight of 0.38 g is to be placed in the opposite pan to balance the pull on the frame. Calculate the surface tension of the soap solution. Giveng=980cms−2.
View Solution
Knowledge Check
A film of soap solution is formed in a rectnagular wire frame of length 10 cm and breadth 5 cm . The surface energy of the film , if the surface tension of soap solution is 0.035 N/m is
A5.5×10−4 JB3.5×10−4 JC1.75×10−4 JD2.75×10−4 JA square frame of side L is dipped in a soap solution .When it is taken out of the solution . When it is take out of the solution , a film is formed on it . If the surface tension is T, then force acting on it is :
A2TLB16TLC4TLD8TLA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
 A2TlgBTlgCTl22gDTl2g
A2TlgBTlgCTl22gDTl2g
Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
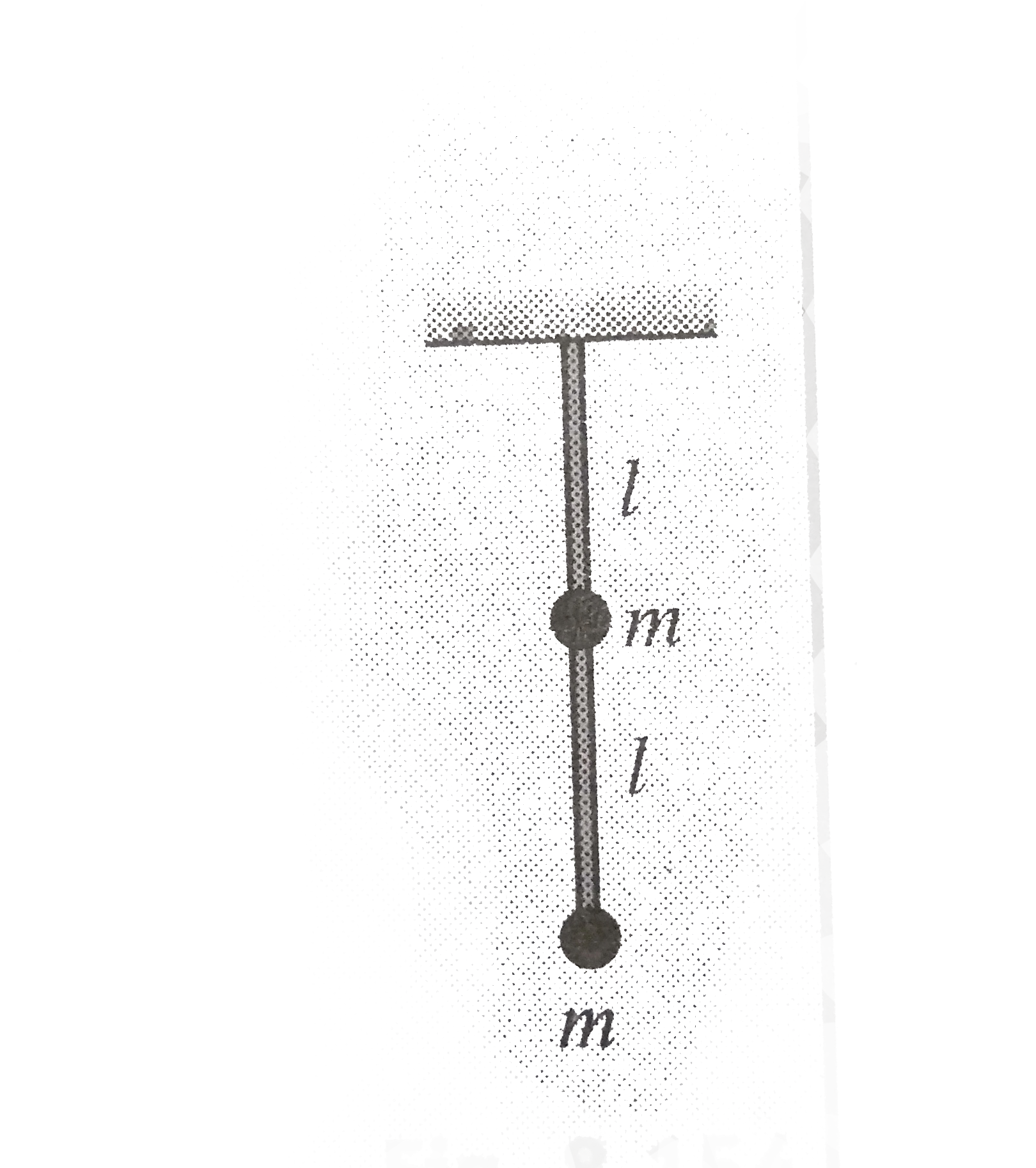
View SolutionA soap film is formed on a rectangular frame of 7 cm side dipping into a scop solution. The frame hangs from the arm of a balance. An extra weight of 0.4 gram is to be placed in the opposite pan to balance the pull on the frame. Caluclate the surface tension of the soap solution.
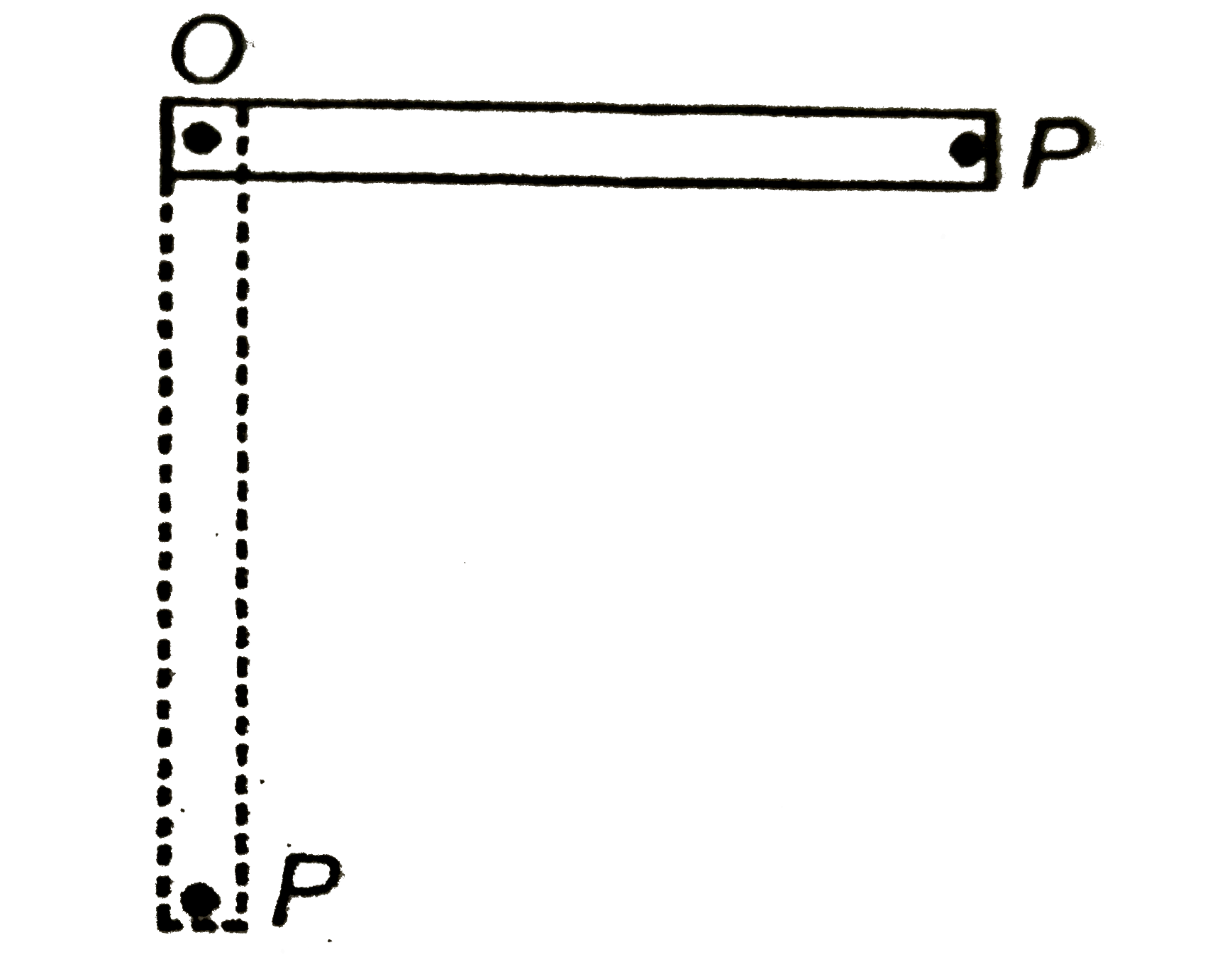
View SolutionA rod of mass m and length L is pivoted at a point O and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotates freely about the point O in downward direction. When it becomes vertical
View SolutionA wire is bent in the form of a U-shape and a slider of negligible mass is connecting the two vertical sides of the U-shape. This arrangement is dipped in a soap solution and lifted a thin soap film is formed in t he frame it supports a wegith of 2.0×10−2 if the length of the slider is 40 cm whta is the surface tension of the film?
View SolutionA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
View Solution

