A plank of mass 10 kg lies on a smoth horizontal surface .A constant forces F= 400 N is is applied on the plank as shown in the figure .(g=10m/s2)
match the statements from Table -1 with the the values in Table -2 and select the correct answer using the code given below.
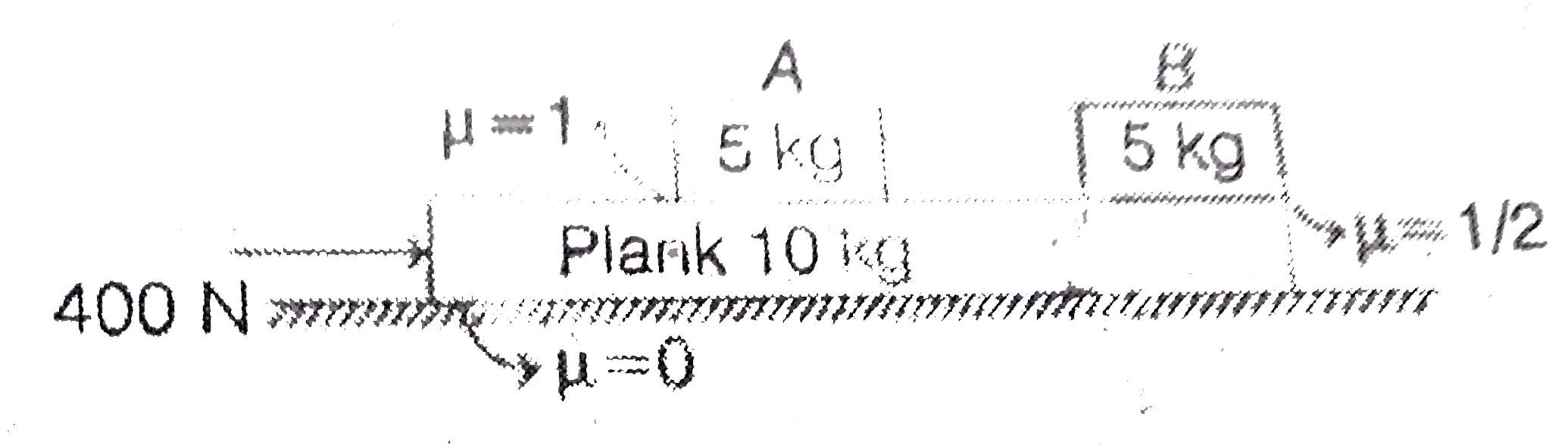

The correct Answer is:(A) (R ) ,(B ) S,(C ) Q,(D)P
Step by step video, text & image solution for A plank of mass 10 kg lies on a smoth horizontal surface .A constant forces F= 400 N is is applied on the plank as shown in the figure .(g=10 m//s^(2)) match the statements from Table -1 with the the values in Table -2 and select the correct answer using the code given below. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
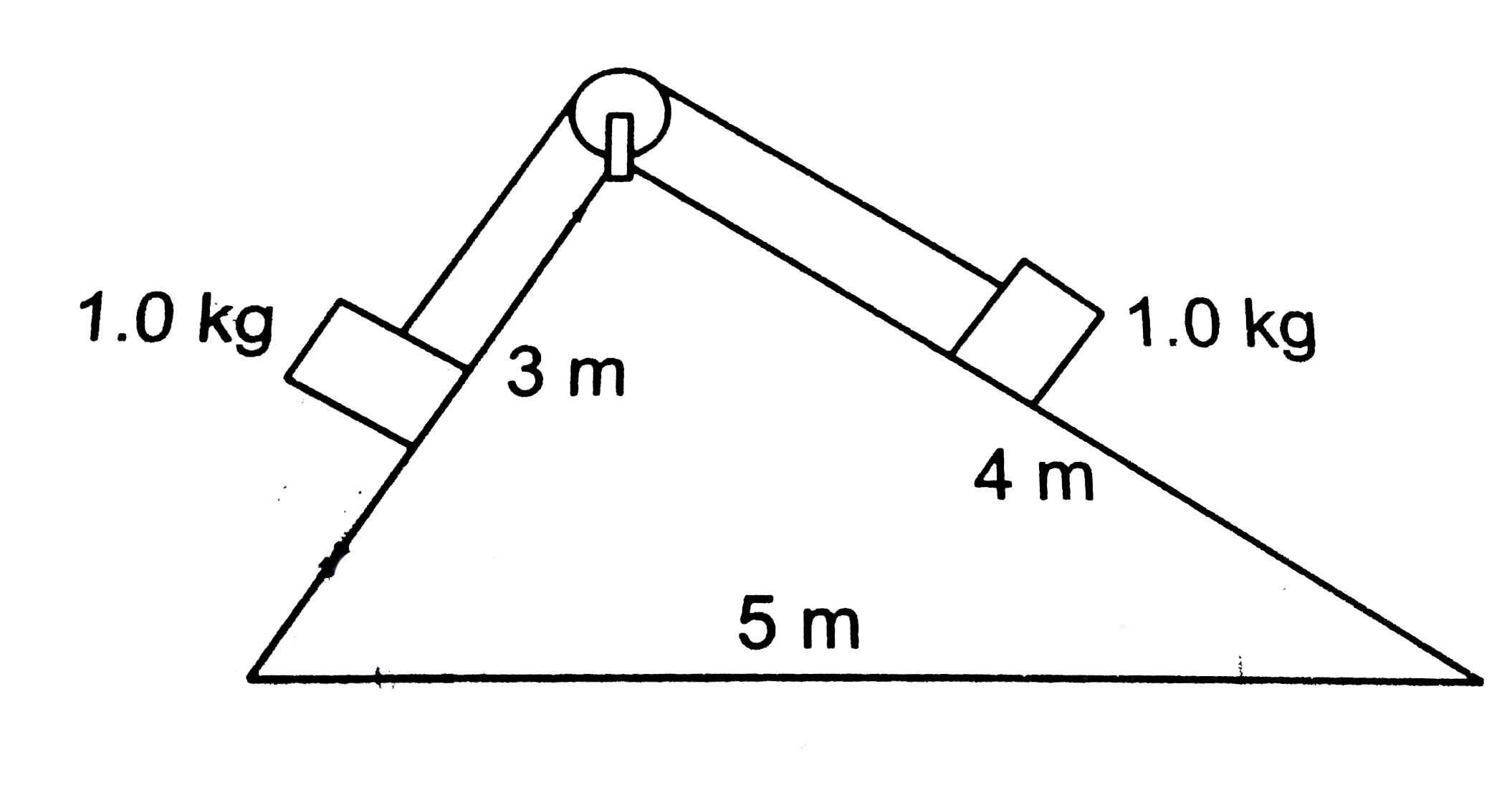
A uniform rod AB of mass 1 kg is supported on a horizontal smooth surface by a small roller of negligible mass and dimension. If the cofficient of friction between end B and vertical wall is 1/3 . The rod is released from rest in the shown position. (Given length of rod =2m, g=10m/s2).Match Table-1 with Table-2 and select the correct answer using the codes given below the lists:

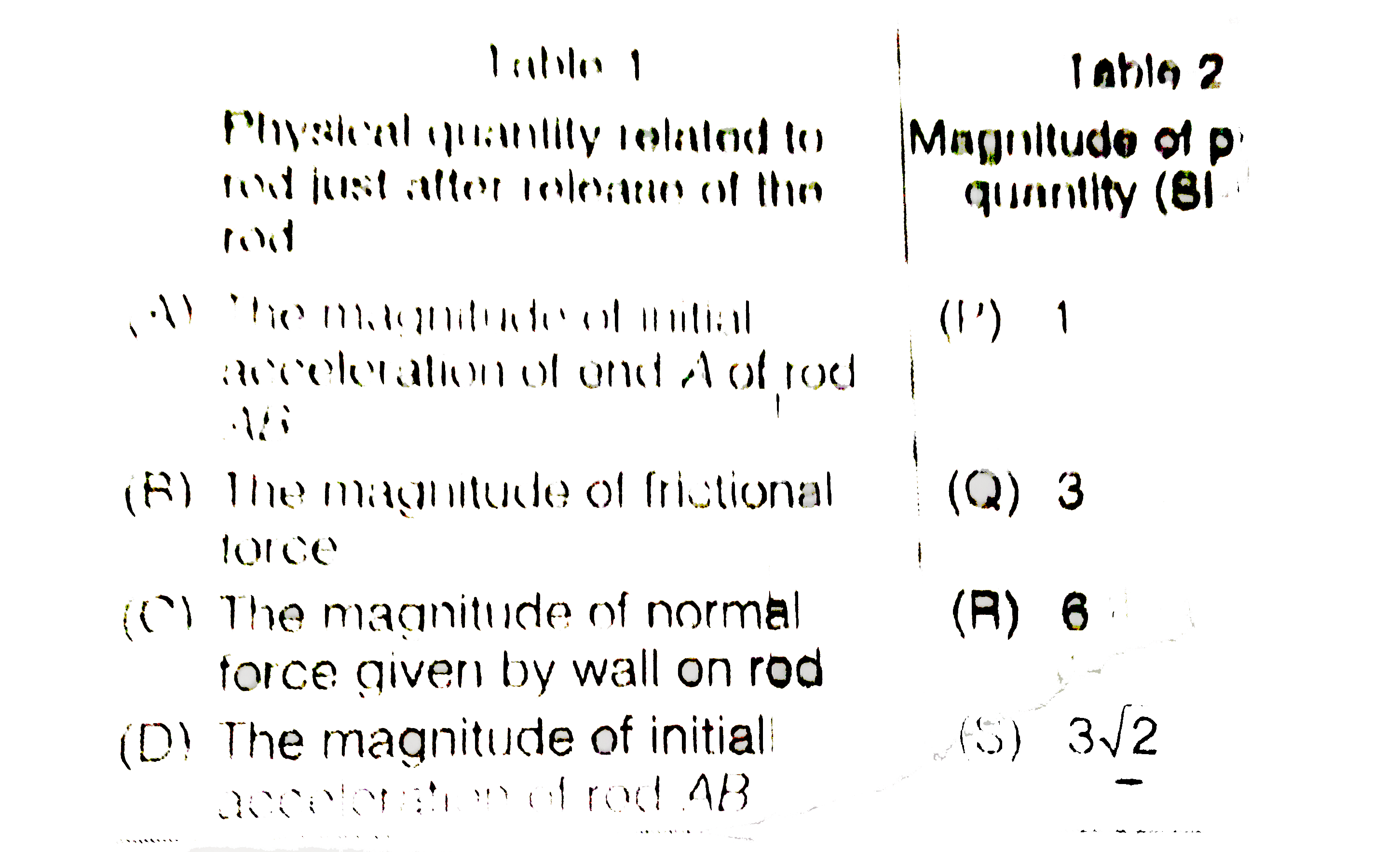
View SolutionA block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View Solution
Knowledge Check
A block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .
 A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2
A5.73m/sec2B8.0m/sec2C3.17m/sec2D10.0m/sec2The uniform rod AB of mass 1 kg is supported on a horizontal smooth surface by a small roller of negligible mass and dimension. If the coefficient of kinetic friction between ends and vertical wall is 1/3. The rod is released from rest in the shown position. (Given length of rod = 2m, g=10m/s2).
Match list-I with List-II and select the correct answer using the codes given below the lists:
 APQRS3124BPQRS1423CPQRS4123DPQRS2341
APQRS3124BPQRS1423CPQRS4123DPQRS2341Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Acceleration of the plank isA3F16mB11F8mC9F4mDZero
A plank of mass 10kg rests on a smooth horizontal surface. Two blocks A and B of masses mA=2kgandmB=1kg lies at a distance of 3m on the plank as shown in the distance of 3m on the plank as shown in the figure. The friction coefficient between the blocks and plank are μA=0.3andμB=0.1. Now a force F = 15 N is applied to the plank in horizontal direction. Find the time after which block A collides with B.
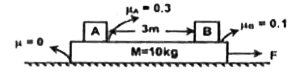
View SolutionA constant force F=m_2g/sisappliedontheblockofmassm_1asshown∈figure.Thestr∈gandthep≤––––yarelightandthesurfaceofthetab≤issm∞th.F∈dtheae≤rationofm_1
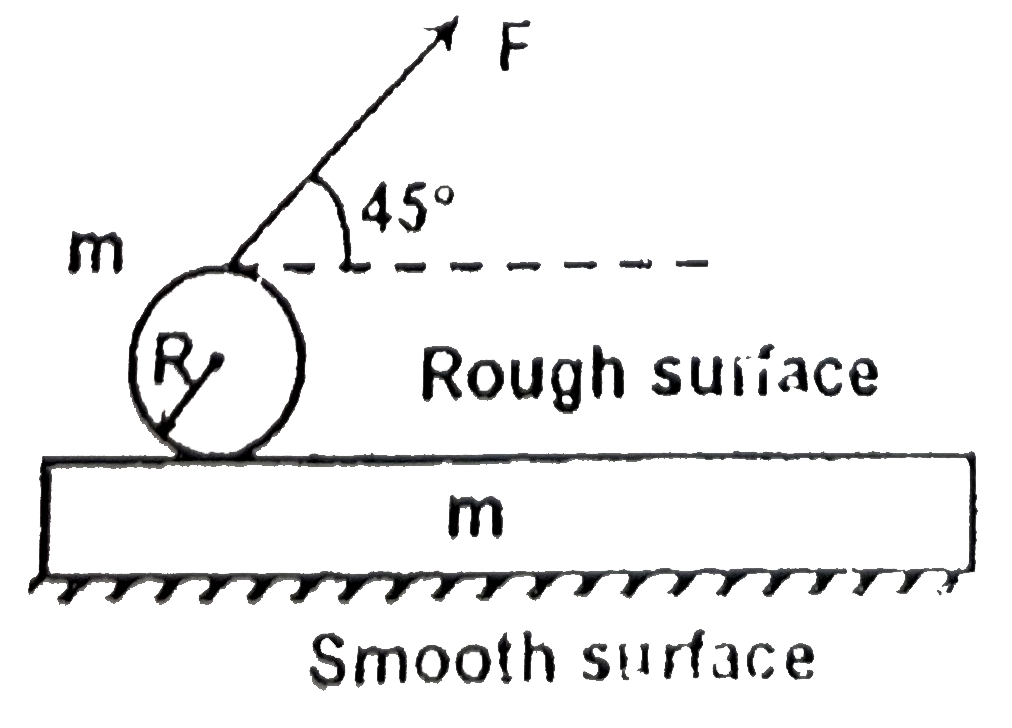
View SolutionA plank of mass m is placed on a smooth surface. Now, a uniform solid sphere of equal mass m and radius R is placed on the plank as shown in the figure. A force F is applied at topmost point of the sphere at an angle of 45∘ to the horizontal. Surface between the plank and the sphere is extremely rough so that there is no slip between the plank and the sphere. The force of firction acting between the plank and the sphere is Fk√2. Find the value of k.
View SolutionA block of mass'm' it kept over the smooth surface of the plank of mass M. the plank of length l is kept over the smooth horizontal surface. A constant horizontal force F is applied onto the plank as shown in figure. Calculate the time after which the block falls off the plank?

View SolutionTwo blocks of masses 2 kg and 4 kg are in close contact on a frictionless horizontal table. A horizontal force of 18 N is applied to the larger mass. What is the force at the surface of contact between the blocks?
View Solution

