Question

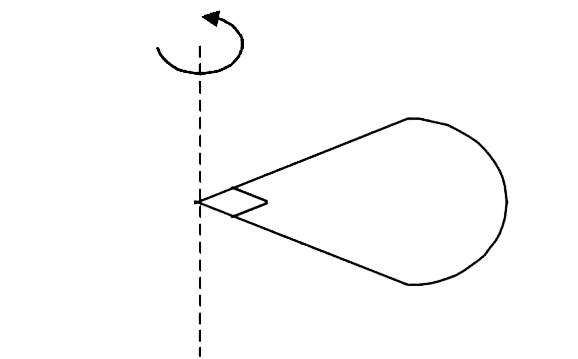
One quarter sector is cut from a uniform disc of radius R. This sector has mass M. It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. What is its moment of inertia about the axis of rotation ?

Options

A. `(MR^(2))/(8)`
B. `sqrt2MR^(2)`
C. `(MR^(2))/(4)`
D. `(MR^(2))/(2)`

Answer

D

Explanation

To find the moment of inertia of a quarter sector cut from a uniform disc of radius $$R$$ and mass $$M$$ about an axis perpendicular to its plane and passing through the center of the original disc, we can follow these steps:

1. Identify the mass of the full disc:
Since the mass of the quarter sector is \( M \), the mass of the full disc can be calculated as:
\( M_{\text{full}} = 4M \)
This is because a quarter of the disc has \( \frac{1}{4} \) of the total mass.

2. Calculate the moment of inertia of the full disc:
The moment of inertia \( I \) of a full disc about an axis passing through its center and perpendicular to its plane is given by the formula:
\( I_{\text{full}} = \frac{1}{2} M_{\text{full}} R^2 \)
Substituting \( M_{\text{full}} = 4M \):
\( I_{\text{full}} = \frac{1}{2} (4M) R^2 = 2MR^2 \)

3. Determine the moment of inertia of the quarter sector:
The moment of inertia of the quarter sector about the same axis can be found by taking \( \frac{1}{4} \) of the moment of inertia of the full disc since the mass of the quarter sector is \( M \) (which is \( \frac{1}{4} \) of the full mass):
\( I_{\text{quarter}} = \frac{1}{4} I_{\text{full}} = \frac{1}{4} (2MR^2) = \frac{1}{2} MR^2 \)

4. Final Result:
Therefore, the moment of inertia of the quarter sector about the specified axis is:
\( I_{\text{quarter}} = \frac{1}{2} MR^2 \)