Two linear harmonic motions of equal amplitudes and frequencies ω and 2 ω imposed on a particle along the axes of x and y respectively. If the initial phase difference between them is π/2, then find the resultant path followed by the particle.
Step by step video & image solution for Two linear harmonic motions of equal amplitudes and frequencies omega and 2 omega imposed on a particle along the axes of x and y respectively. If the initial phase difference between them is pi//2, then find the resultant path followed by the particle. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBook:SL ARORAChapter:OSCILLATIONSExercise:Problems for self practice
Explore 67 Videos
- OSCILLATIONSBook:SL ARORAChapter:OSCILLATIONSExercise:Exercise
Explore 233 Videos
- OSCILLATIONSBook:SL ARORAChapter:OSCILLATIONSExercise:Example
Explore 202 Videos
- MOTION IN ONE DIMENSIONBook:SL ARORAChapter:MOTION IN ONE DIMENSIONExercise:problems for self practice
Explore 66 Videos
- Physical worldBook:SL ARORAChapter:Physical worldExercise:Exercise
Explore 49 Videos
Similar Questions
Two linear SHM of equal amplitudes A and frequencies ω and 2ω are impressed on a particle along x and y−axes respectively. If the initial phase difference between them is π/2. Find the resultant path followed by the particle.
View SolutionThe maximum seperation between two particles executing simple harmonic motion of the equal amplitude and same frequency along the same straight line and about the same mean position, is √3 times the amplitude of oscillation. IF the phase difference between them is ϕ, determine 2π/ϕ.
View Solution
Knowledge Check
Two linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
Aa circleBa straight lineCan ellipseDa parabolaTwo simple harmonic motions y1=Asinωt and y2=Acosωt are supre imposed on a particle of mass m.
A12mω2A2Bmω2A2C14mω2A2DzeroTwo simple harmonic motions with the same frequency act on a particle at right angles i.e., along X-axis and Y-axis. If the two amplitudes are equal and the phase difference is π/2, the resultant motion will be
Aa circleBan ellipse with the major axis along Y-axisCan ellipse with the major axis along X-axisDa straight line inclined at 45∘ to the X-axis
Two particles perform linear simple harmonic motion along the same path of length 2 A and period T as shown in the graph below. The phase difference between them is
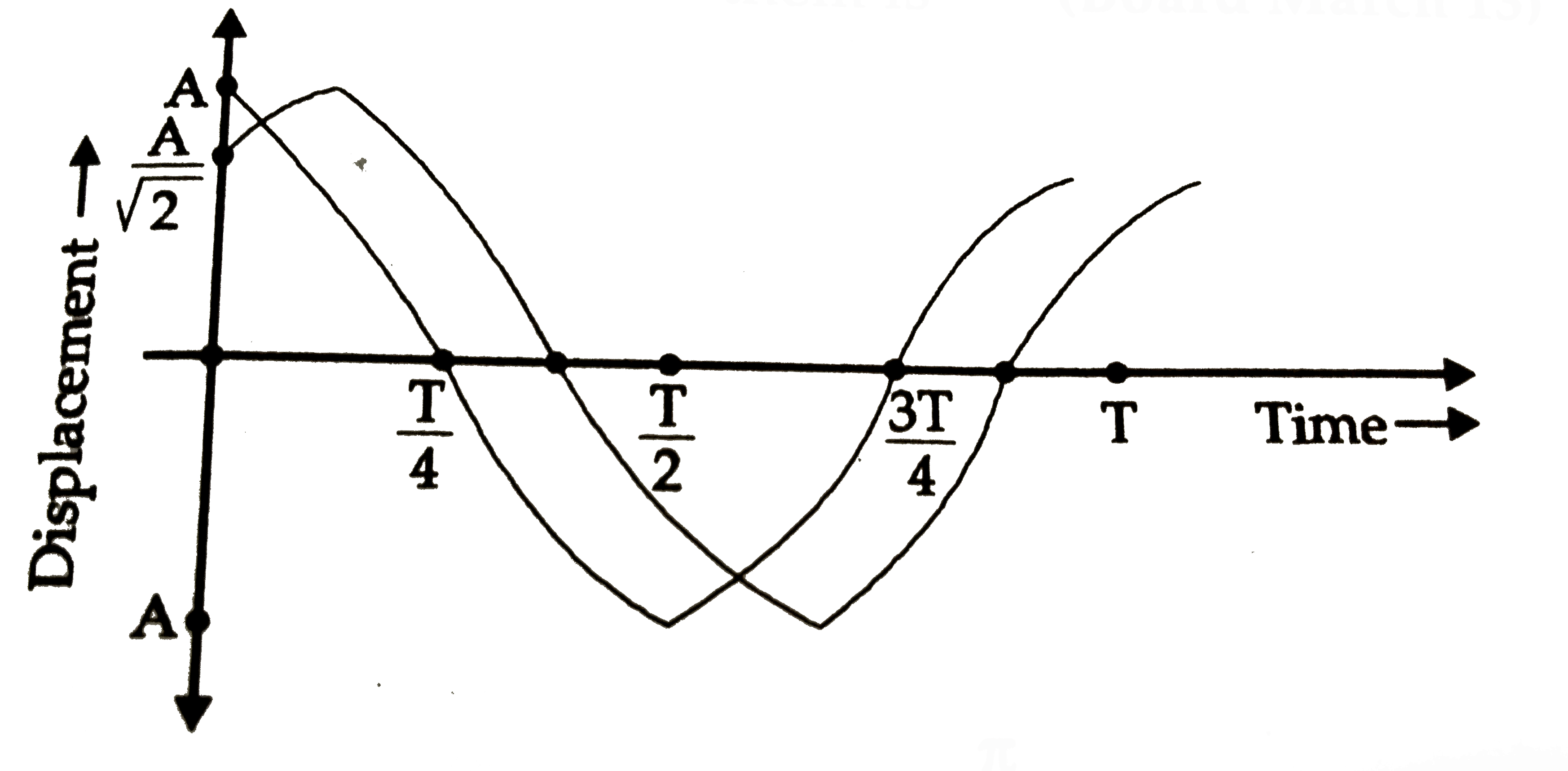
View SolutionA particle is subjected to two simple hasrmonic motions in the same direction having equal amplitudes and equal frequency. If the resultant amplitude is equal to the amplitude of the individual motions, find the phase difference between the individual motions.
View SolutionTwo simple harmonic motions y1=Asinωt and y2 = Acosωt are superimposed on a particle of mass m. The total mechanical energy of the particle is
View SolutionA particle executing simple harmonic motion with an amplitude A and angularr frequency ω. The ratio of maximum acceleration to the maximum velocity of the particle is
View SolutionTwo simple harmonic motions are given by x1=asinωt+acosωt and x2=asinωt+a√3 01. The ratio of the amplitudes of first and second motion and the phase difference between them are respectively
View Solution

