Assertion: Two blocks A and B are connected at the two ends of an ideal spring as shown in figure. Initially, spring was released. Now block B is pressed. Linear momentum of the system will not remain constant till the spring reaches its initial natural length.
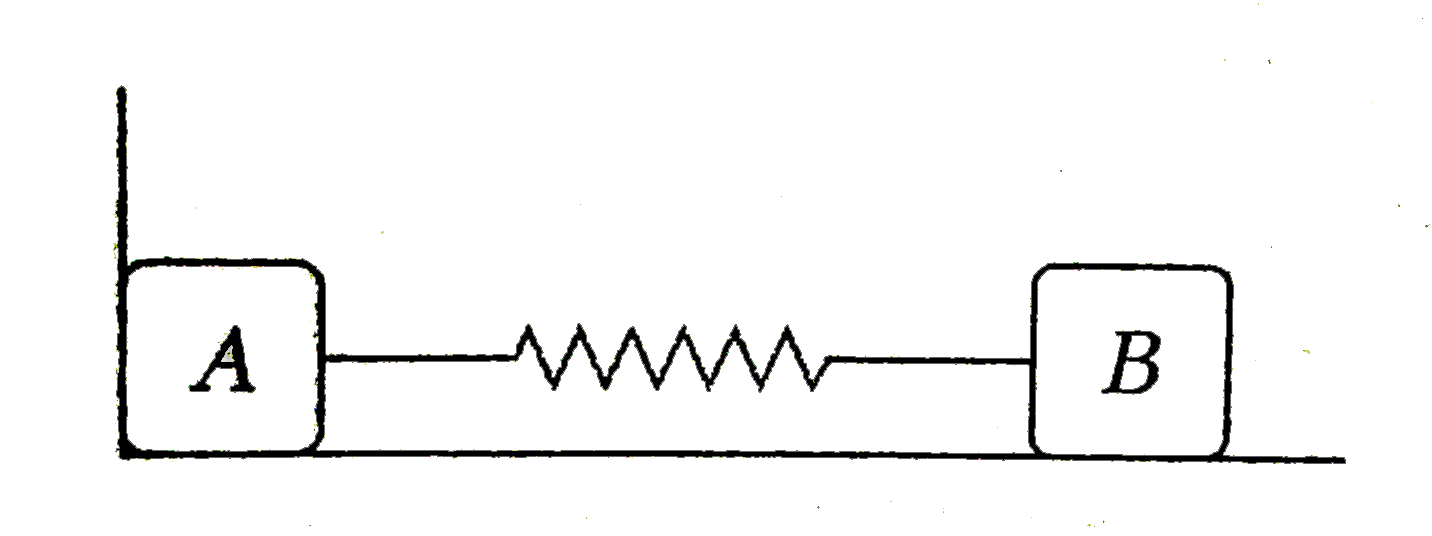
Reason: An external force will act from the wall on block A.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
Linear momentum will not remain constant till spring will remain compressed. Therefore a force will act on block A from the wall.
Topper's Solved these Questions
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Match the coloumns
Explore 9 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Taking it together
Explore 73 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
Similar Questions
Two blocks having masses 8kg and 16kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects B with ceiling as shown in the figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contact with ground?

View SolutionTwo blocks having masses 8kg and 16 kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible starting also connects B with ceiling as shown in figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contant with ground
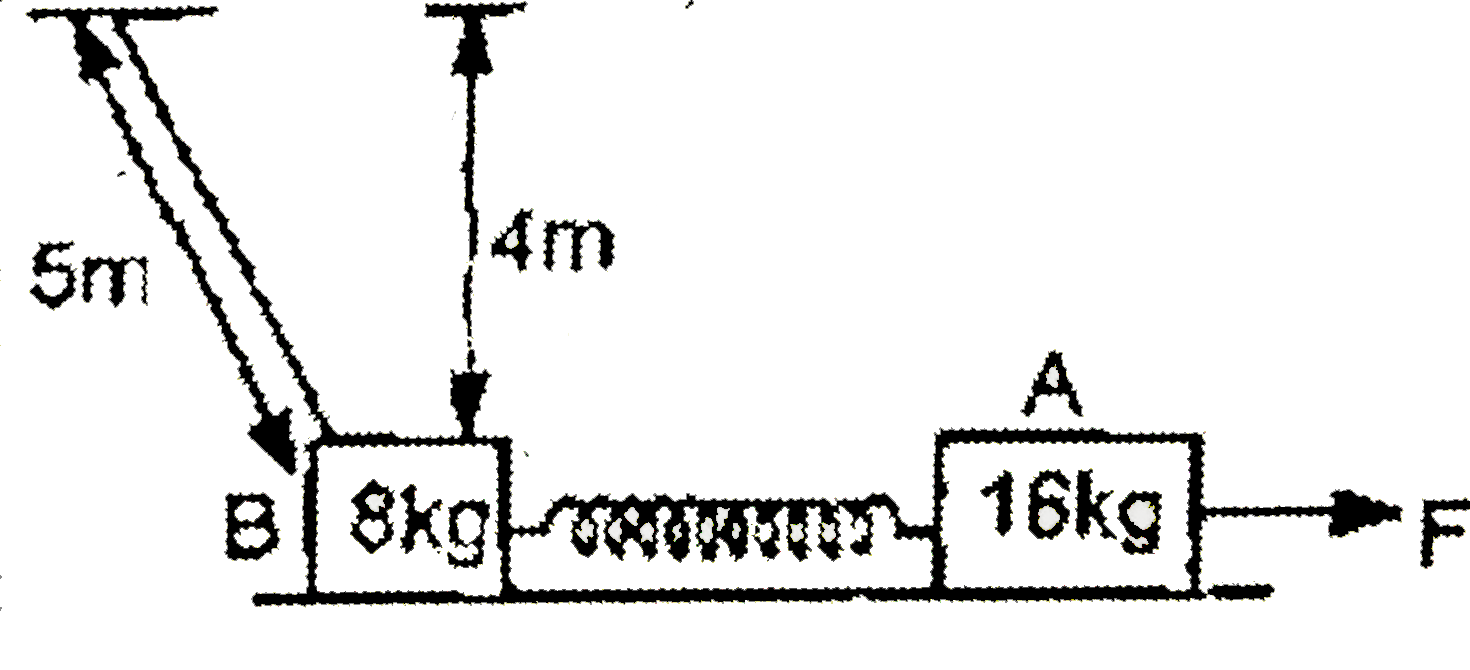
View Solution
Knowledge Check
Assertion: Two blocks A and B are connected at the two ends of an ideal spring as shown in figure. Initially, spring was released. Now block B is pressed. Linear momentum of the system will not remain constant till the spring reaches its initial natural length.

Reason: An external force will act from the wall on block A.AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.CIf Assertion is true but Reason is false.DIf Assertion is false but Reason is true.Two masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length
 Aenergy of smaller body will be 20 JBenergy of smaller body will be 40 JCenergy of smaller body will be 10 JDenergy of both the bodies will be same
Aenergy of smaller body will be 20 JBenergy of smaller body will be 40 JCenergy of smaller body will be 10 JDenergy of both the bodies will be sameFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mg
In the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View SolutionTwo blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion
View SolutionThe system of the wedge and the block connected by a massless spring as shown in the figure is released with the spring in its natural length. Friction is absent. Maximum elongation in the spring will be
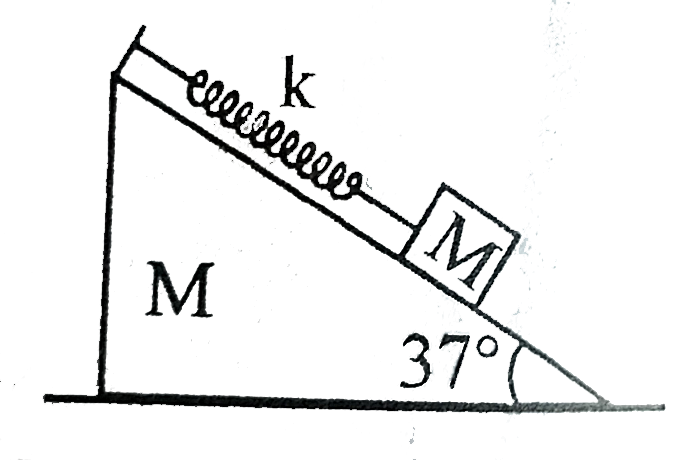
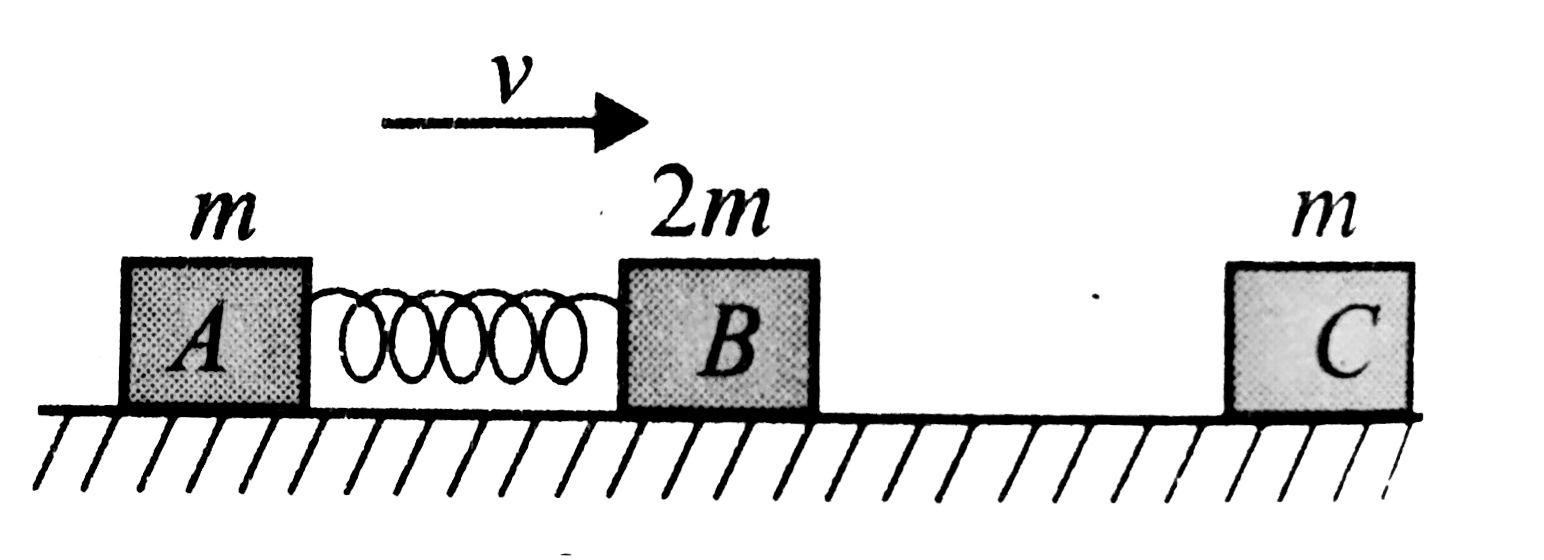
View SolutionTwo blocks A and B of masses in and 2m, respectively, are connected with the help of a spring having spring constant, k as shown in Fig. Initially, both the blocks arc moving with same velocity v on a smooth horizontal plane with the spring in its natural length. During their course of motion, block B makes an inelastic collision with block C of mass m which is initially at rest. The coefficient of restitution for the collision is 1/2. The maximum compression in the spring is
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View Solution

