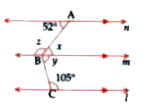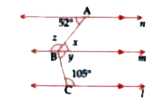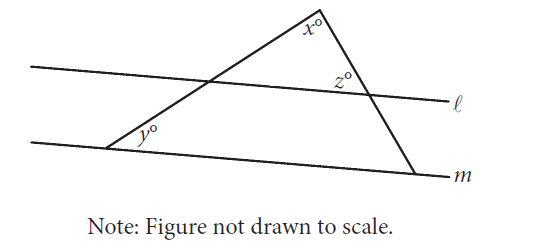
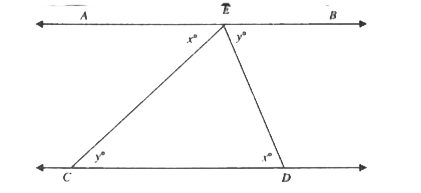
In the figure above, lines l and m are parallel, y = 20, and z = 60. What is the value of x ?
A
120
B
100
C
90
D
80
Video Solution
Text Solution
The correct Answer is:B
Let the measure of the third angle in the smaller triangle be a∘. Since lines l and m are parallel and cut by transversals, it follows that the corresponding angles formed are congruent. So a∘=y∘=20∘. The sum of the measures of the interior angles of a triangle is 180∘, which for the interior angles in the smaller triangle yields a + x + z = 180. Given that z = 60 and a = 20, it follows that 20 + x + 60 = 180. Solving for x gives x = 180 − 60 − 20, or x = 100.
Choice A is incorrect and may result from incorrectly assuming that angles x + z = 180. Choice C is incorrect and may result from incorrectly assuming that the smaller triangle is a right triangle, with x as the right angle. Choice D is incorrect and may result from a misunderstanding of the exterior angle theorem and incorrectly assuming that x = y + z.
|
Similar Questions
Knowledge Check
In the figure, lines l and m are parallel. If y−z=60,then what is the value of x?
 A60B75C90D120
A60B75C90D120
In the figure above, lines l and m are parallel and lines s and t are parallel. If the measure of ∠1 is 35∘, what is the measure of ∠2 ?A35∘B55∘C70∘D145∘
In the figure above, if line segment AB is parallel to line segment CD, what is the value of y?A12B15C18D20
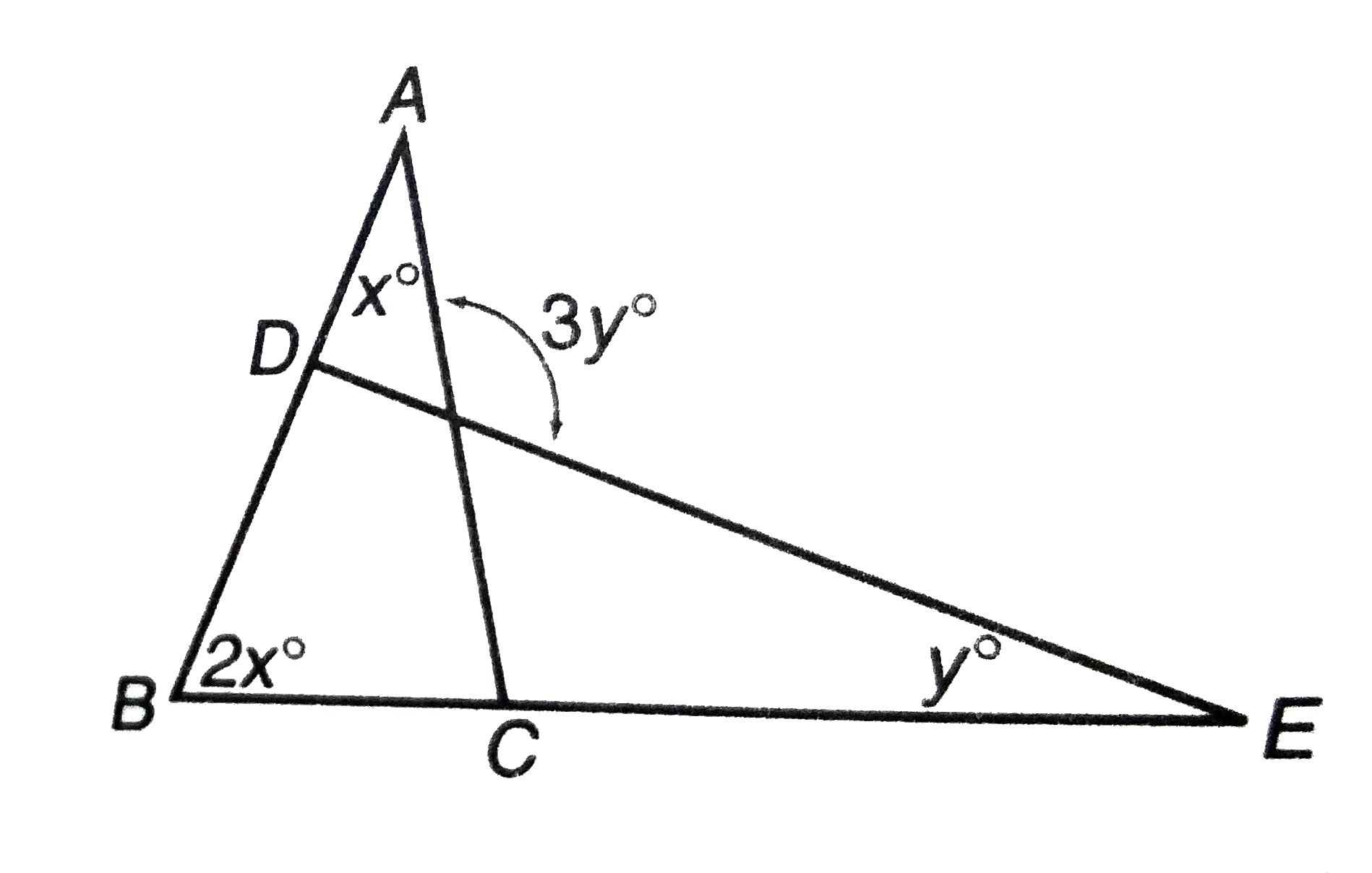
In the figure above, what is y in terms of x?
View Solution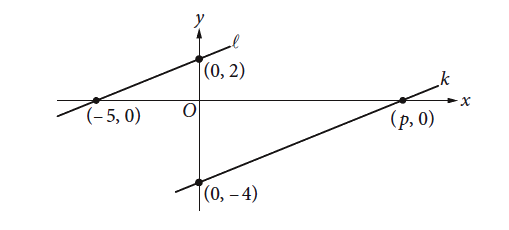
In the xy-plane above, line l is parallel to line k. What is the value of p ?
View Solution
In the figure above, x∣∣y. What is the value of a?
View SolutionIn the figure, AB is parallel to CD. What is the value of x?
View Solution
In the figure above, what is the value of y?
View Solution