A square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find
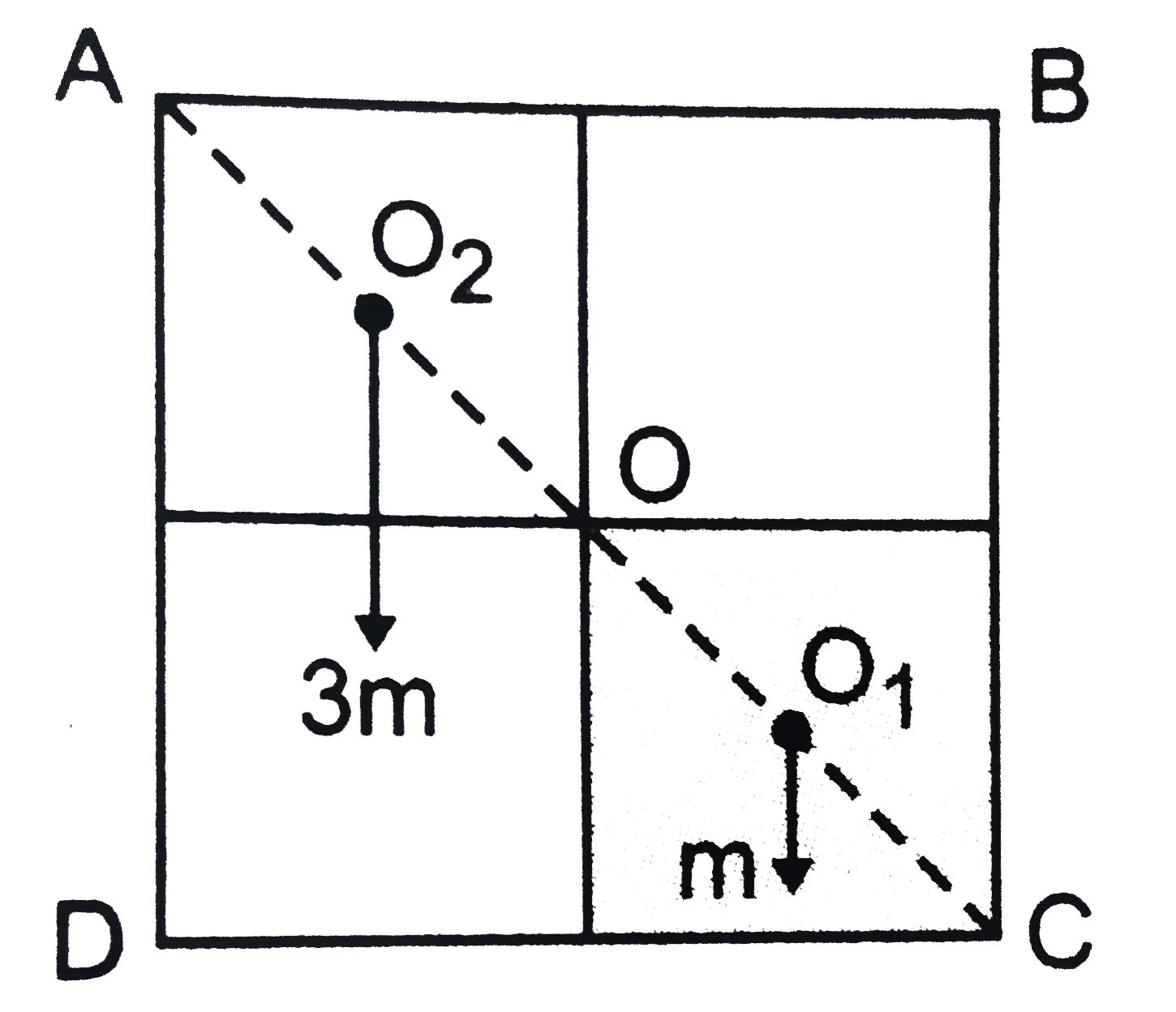
the position of centre of mass of the remaining portion from the centre O.
Step by step video & image solution for A square of side 4 m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find the position of centre of mass of the remaining portion from the centre O. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem
24 Videos
- ROTATIONAL MOTIONBOOK - SL ARORACHAPTER - ROTATIONAL MOTIONEXERCISE - Problem for self practice
90 Videos
- PROPERTIES OF SOLIDSBOOK - SL ARORACHAPTER - PROPERTIES OF SOLIDSEXERCISE - All Questions
97 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
Similar Questions
A square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is √2kcm . Find the value of K.
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.
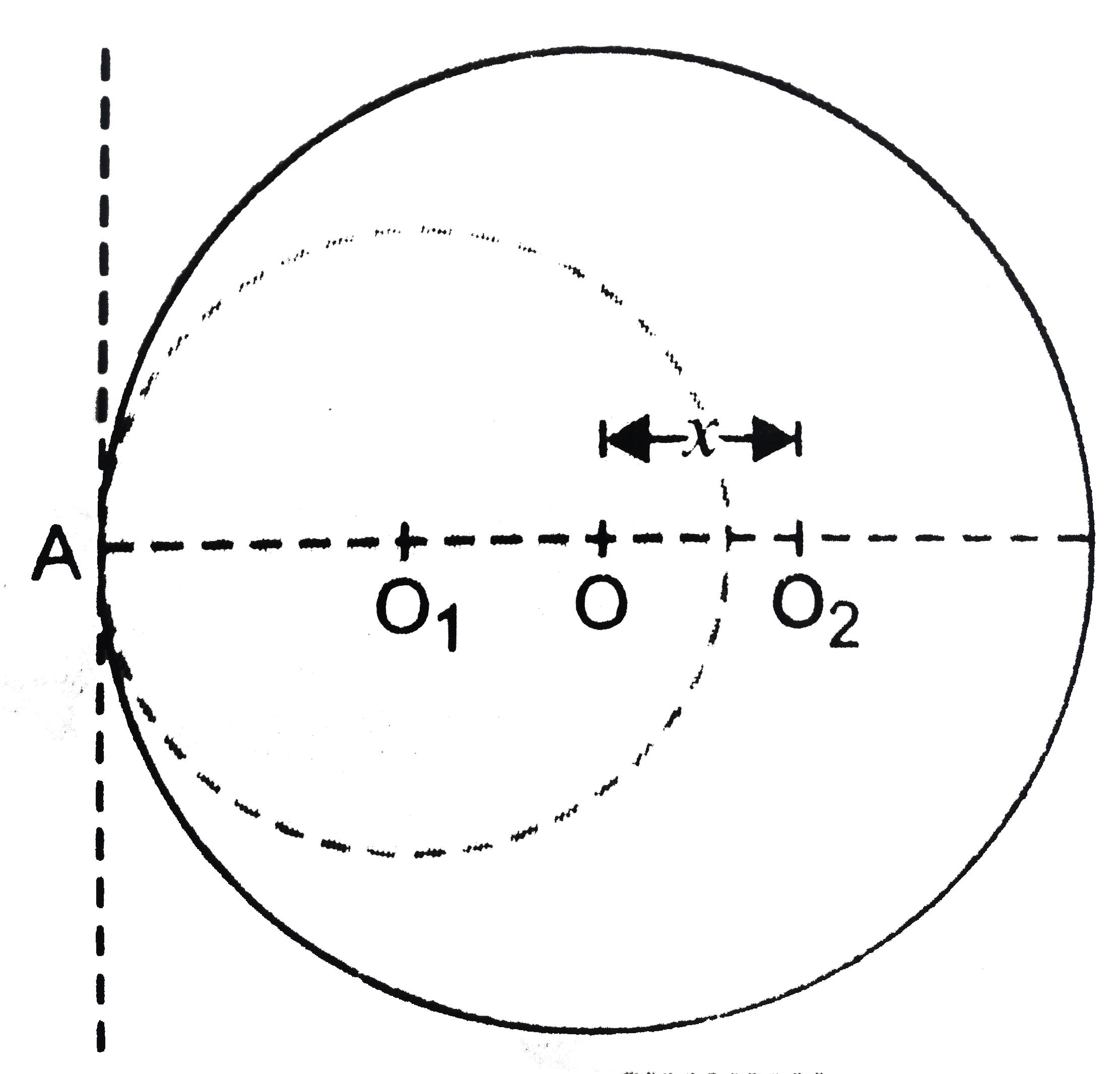
View Solution
Knowledge Check
A square of side a and uniform thickness is divided into four equal parts. If upper right part is removed, then find the coordinates of centre of mass of remaining part.
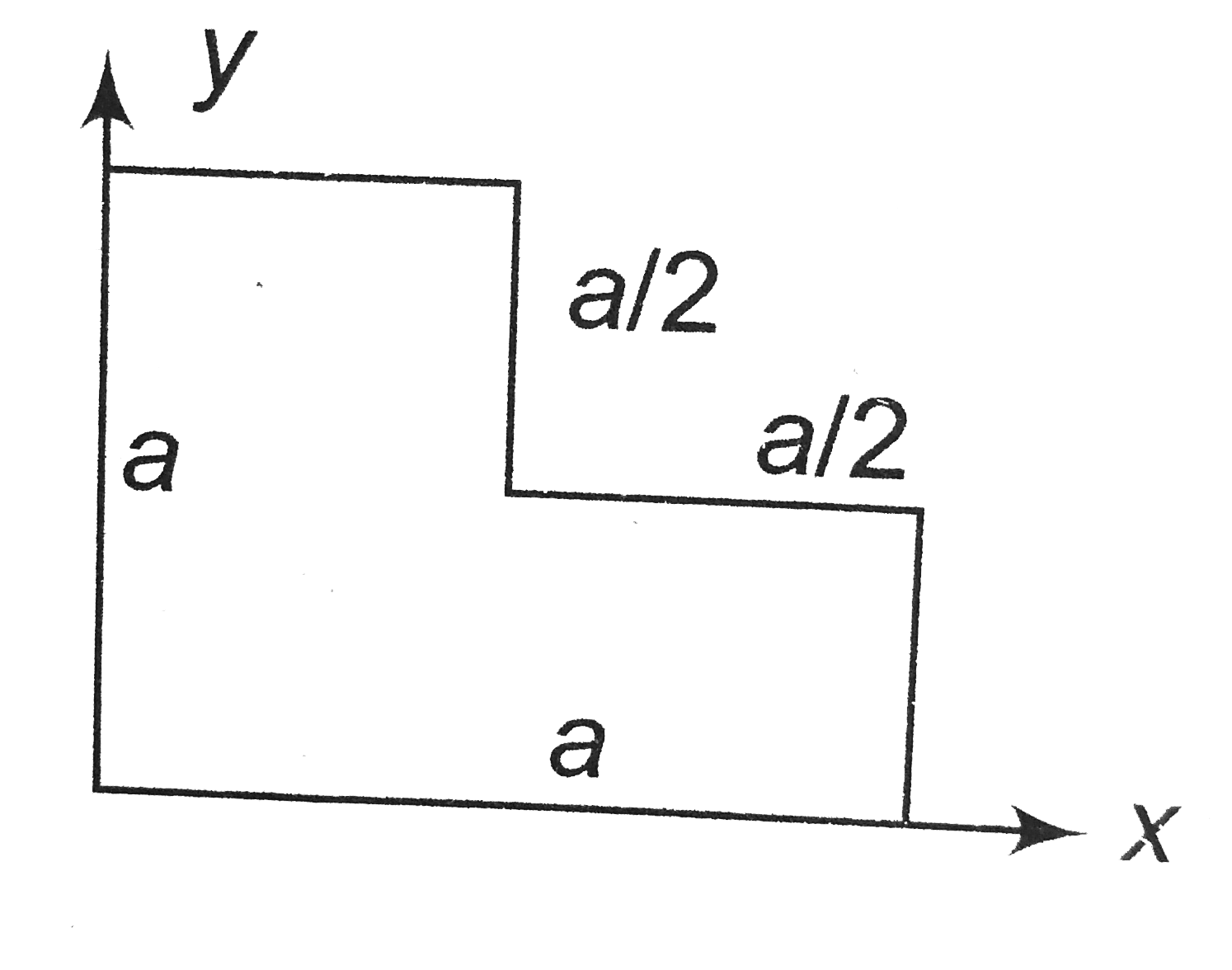 .A(512a,512a)B(712a,712a)C(14a,14a)D(13a,13a)
.A(512a,512a)B(712a,712a)C(14a,14a)D(13a,13a)A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the above
Aat O1Bat OC0.54 cm from O on the left hand sideDNone of the aboveA square of side 2cm and uniform thickness is divided into four squares. The square portion A′AB′D is removed and the removed portion is placed over the portion DB′BC′. The new position of centre of mass is
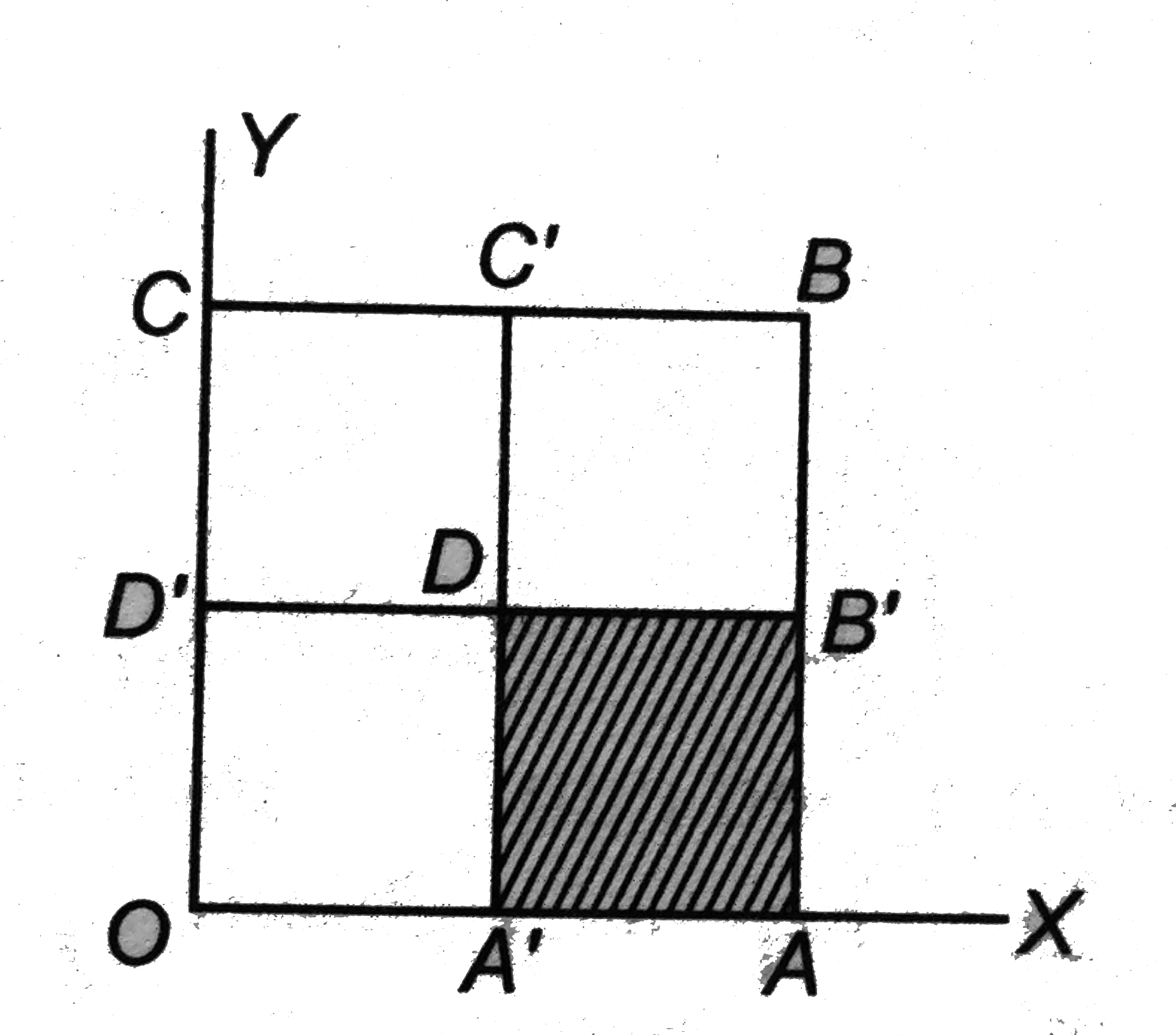 A(2cm,2cm)B(2cm,3cm)C(2cm,2.5cm)D(3cm,3cm)
A(2cm,2cm)B(2cm,3cm)C(2cm,2.5cm)D(3cm,3cm)
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion
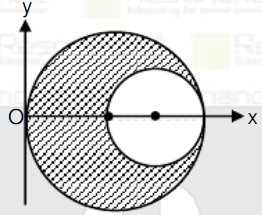
View SolutionFrom a square sheet of uniform density , a portion a removed shown shaded in fig. Find the centre of msas of the remaining portion is the side of the square is α

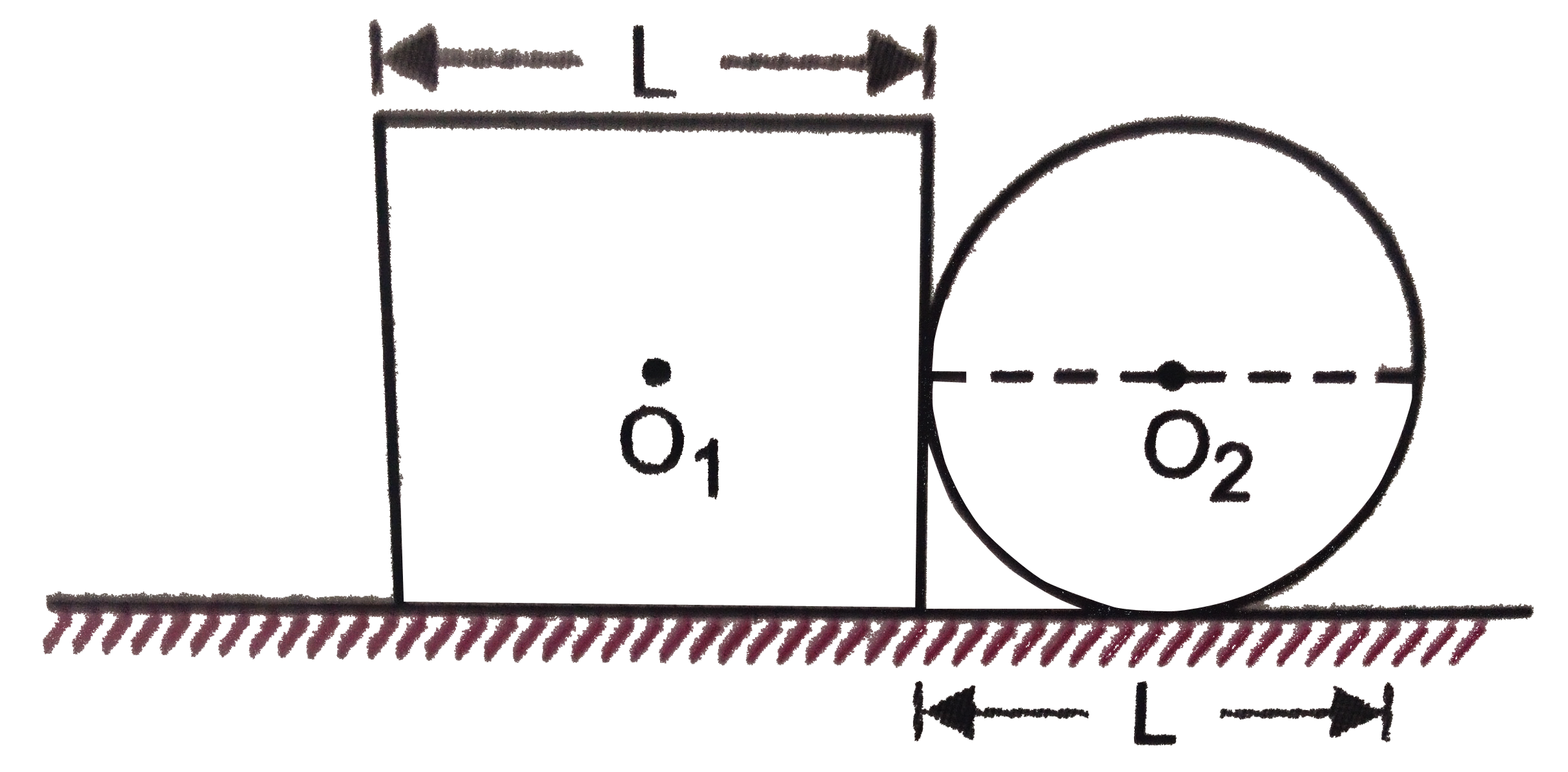
View SolutionA uniform square plate and a disc having same mass per unit area are kept in contact as shown in Fig. The side of square and diameter of circle are both equal to L. Locate the position of centre of mass of the system w.r.t. the centre of the square.
View SolutionA circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

View SolutionFigure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
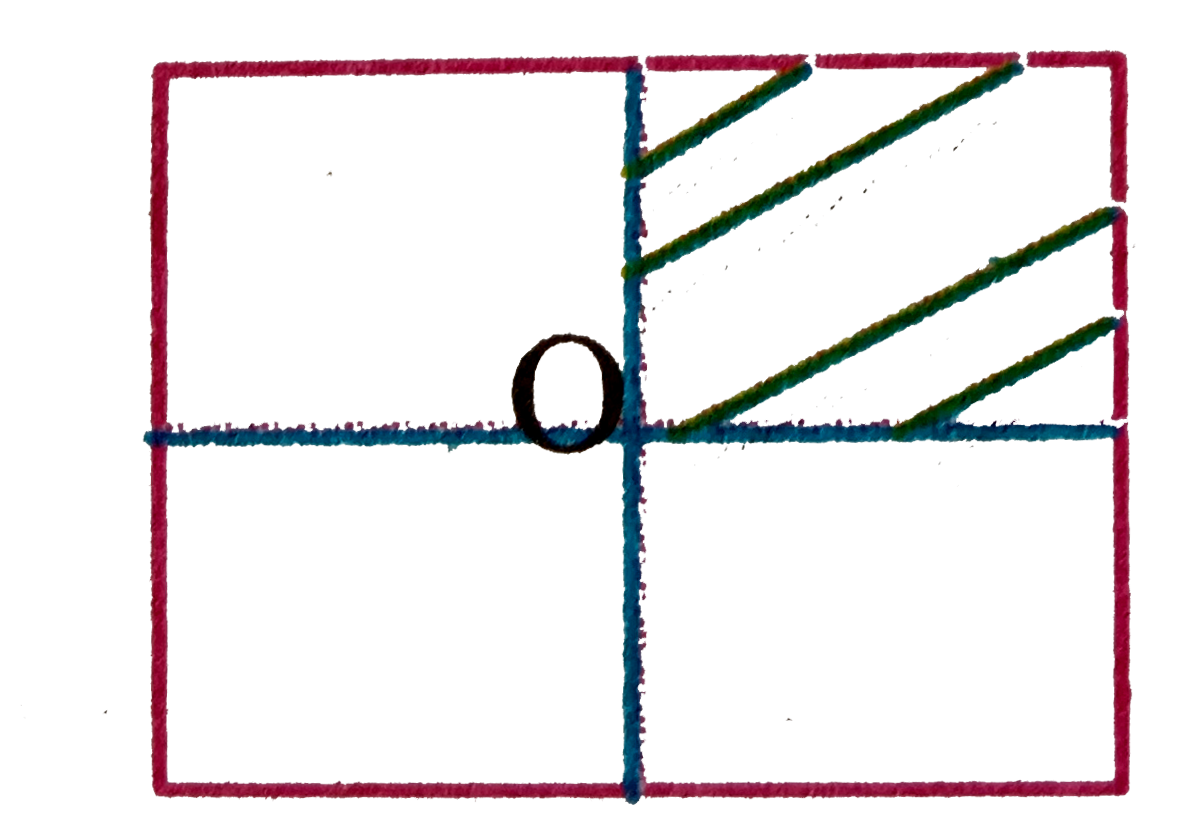
View Solution
