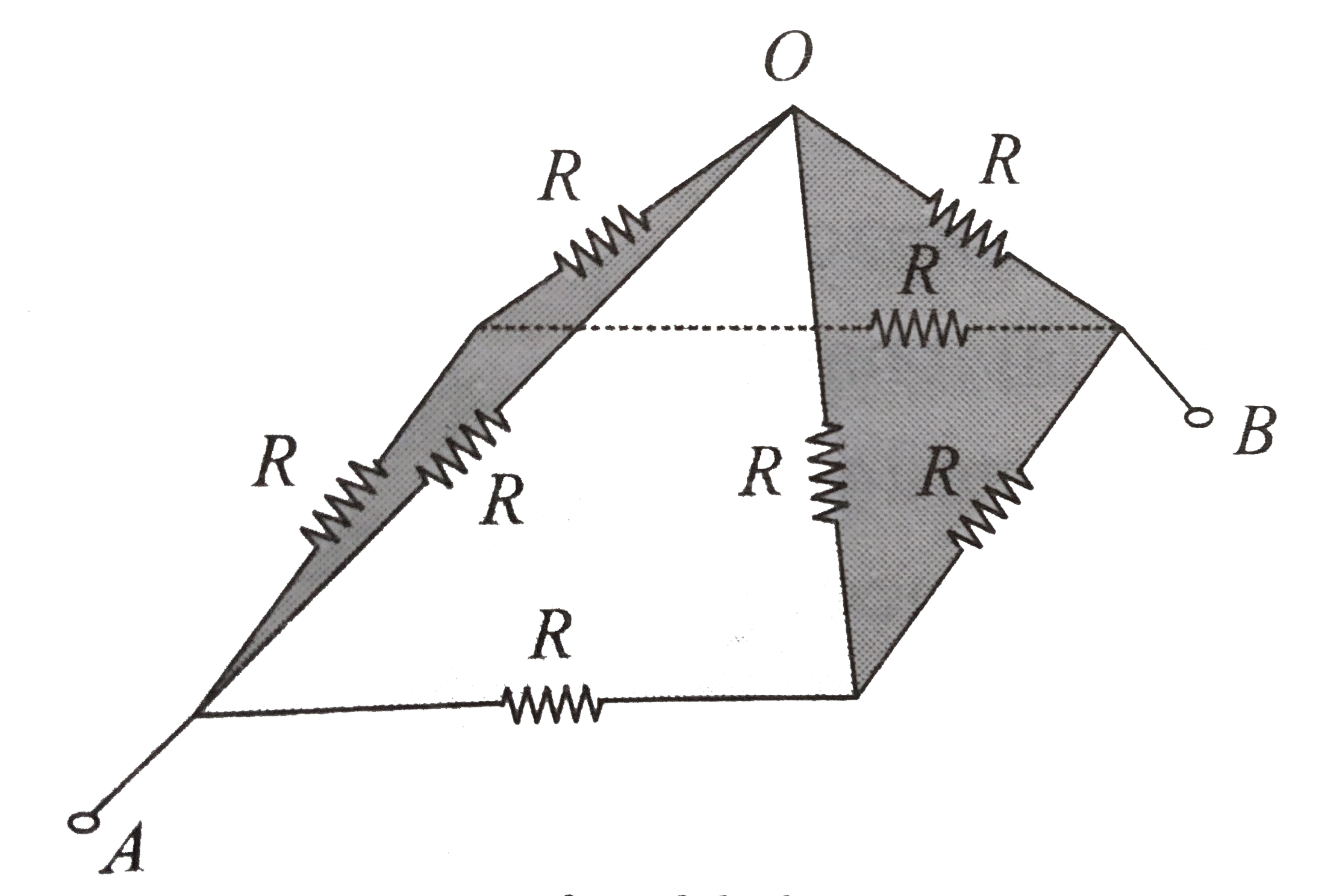
A newtwork of conductors is in the form of a triangle ABC in which AB = 1Ω, BC=2Ω and CA = 3Ω and the angular points A, B and C are joined to any point O inside the triangle by resistance 1Ω, 2Ω and 3Ω, respectively. Find the equivalent resistance between A and B.
[Hing: Assume current at the entrance and exit points].
The correct Answer is:73113=0.65Ω
Step by step video, text & image solution for A newtwork of conductors is in the form of a triangle ABC in which AB = 1Omega, BC=2Omega and CA = 3Omega and the angular points A, B and C are joined to any point O inside the triangle by resistance 1Omega, 2Omega and 3Omega, respectively. Find the equivalent resistance between A and B. [Hing: Assume current at the entrance and exit points]. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FUNDAMENTAL OF CURRENT ELECTRICITYBook:NN GHOSHChapter:FUNDAMENTAL OF CURRENT ELECTRICITYExercise:Exercises
Explore 45 Videos
- ELECTROMAGNETIC INDUCTIONBook:NN GHOSHChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERICISES-B
Explore 18 Videos
- GALVANOMETERS: AMMETER AND VOLTMETERSBook:NN GHOSHChapter:GALVANOMETERS: AMMETER AND VOLTMETERSExercise:Exercise
Explore 32 Videos
Similar Questions
Knowledge Check
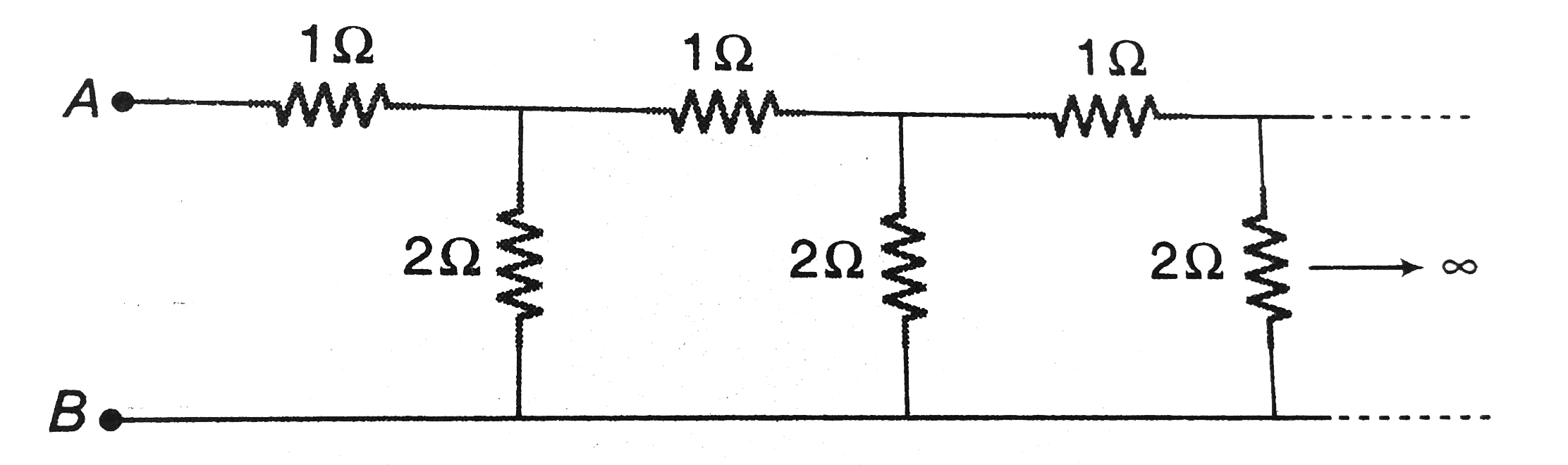
Equivalent resistance between the points A and B (in Ω)
 .A15B114C213D312
.A15B114C213D312The correct combination of three resistances 1Ω,2Ωand3Ω to get equivalent resistance 115Ω is
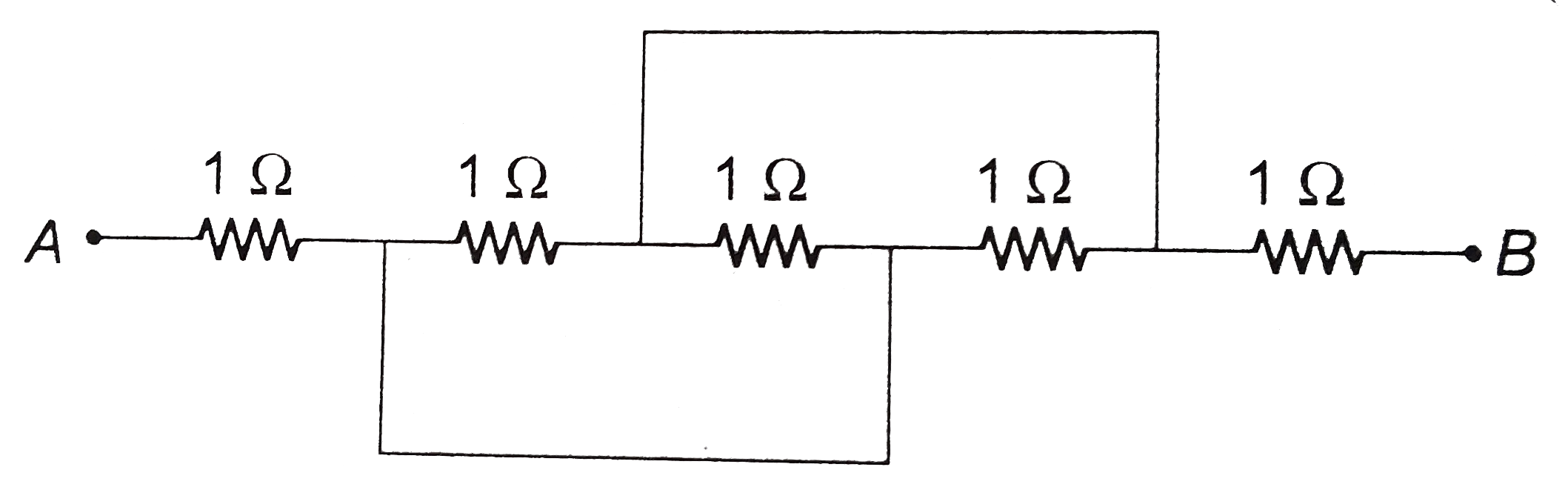
AAll three are combines in paralleBAll three are combines in paralleC1Ωand2Ω in parallel and 3Ω is in series to bothD2Ωand3Ω in parallel and 1Ω is in series to bothIn the given figure, R=3Ω. Determine equivalent
resistance between points A and B.
 . A3ΩB2ΩC15ΩD6Ω
. A3ΩB2ΩC15ΩD6Ω
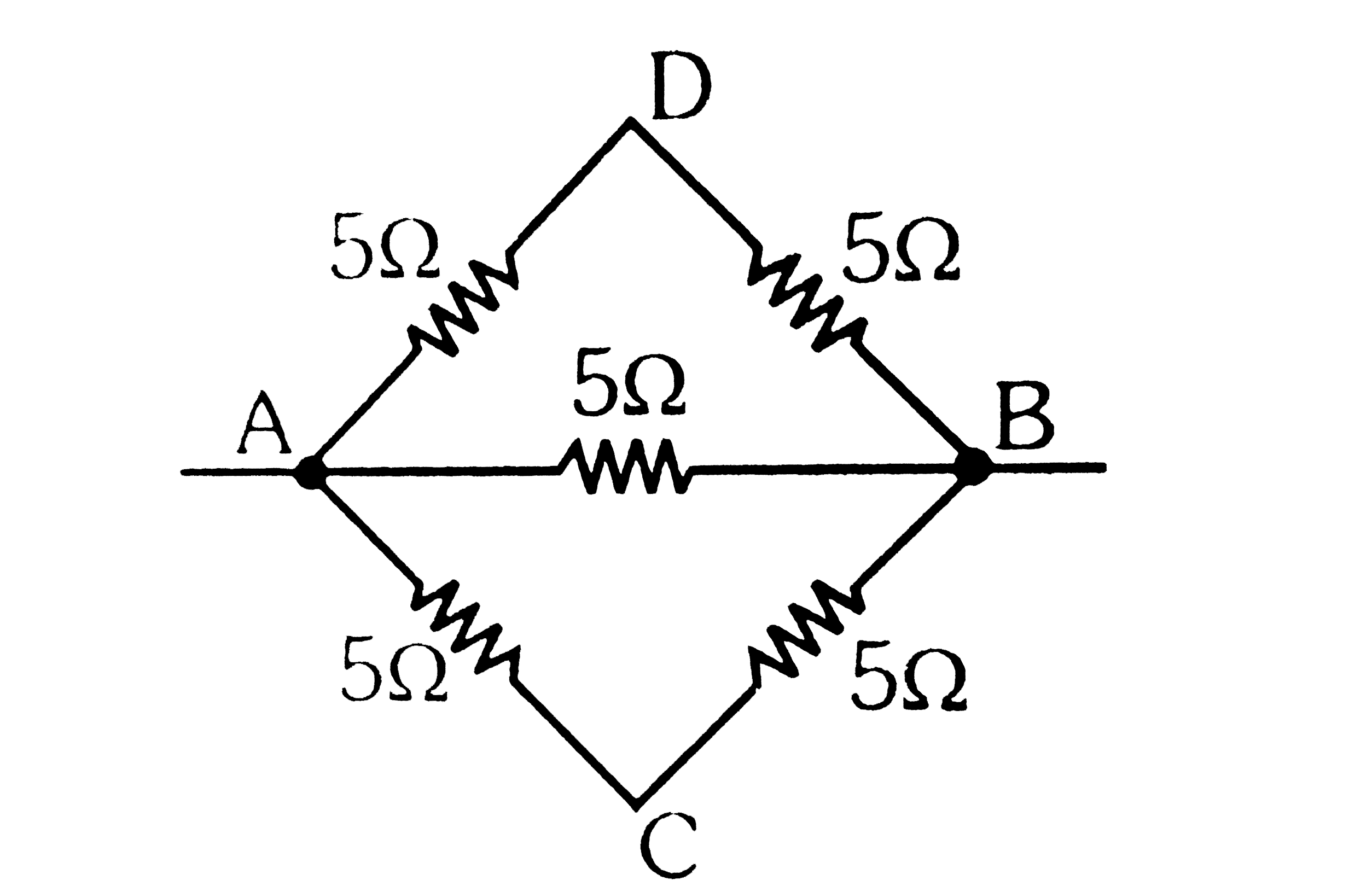
Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
View SolutionEach resistance shown in figure is 2Ω. The equivalent resistance between A and B is
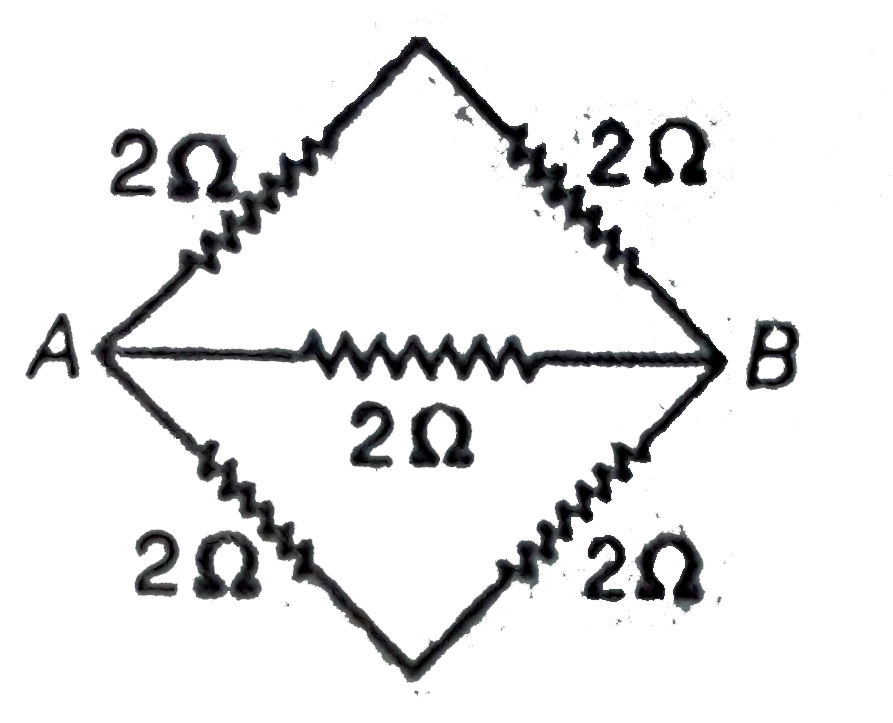
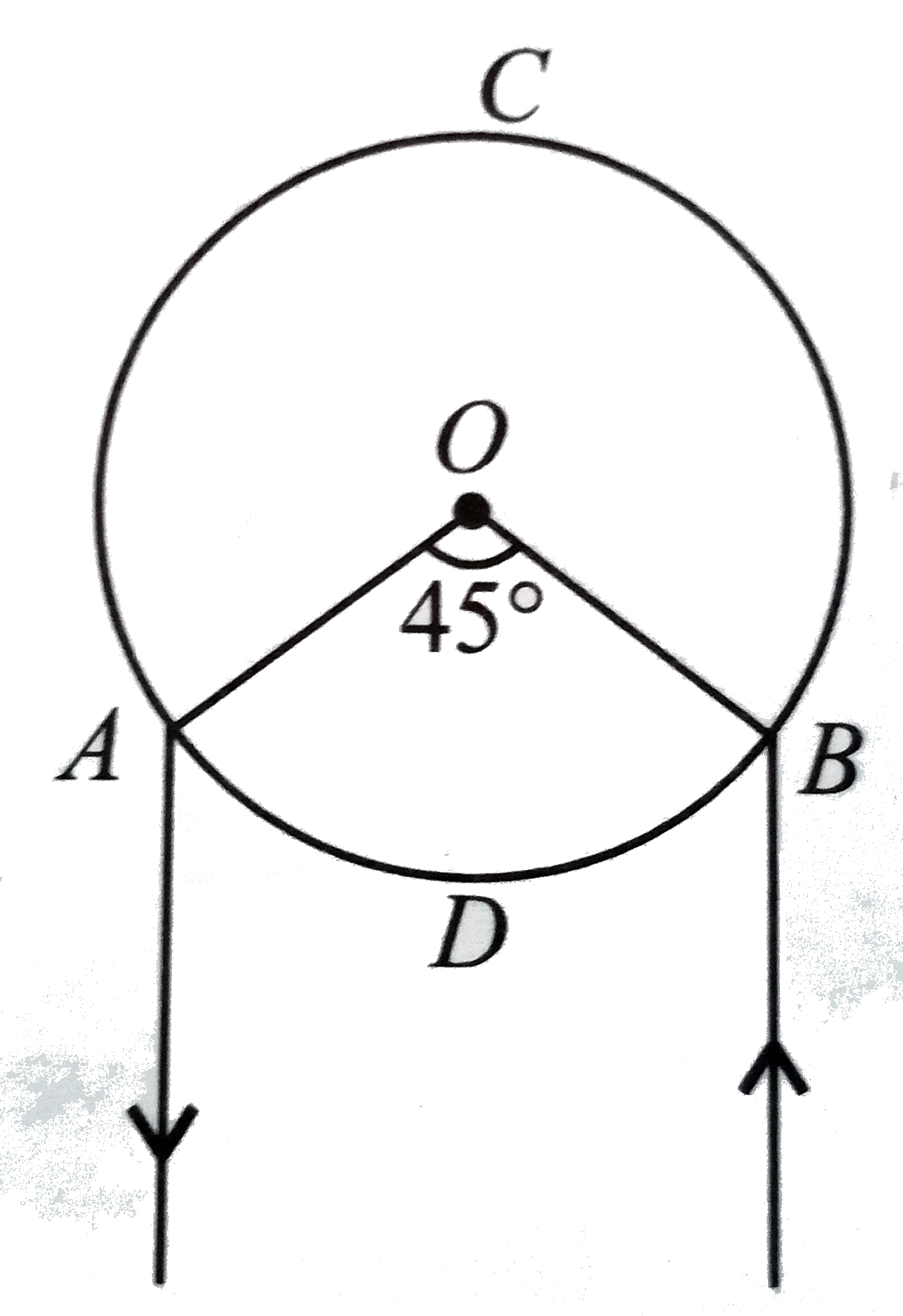
View SolutionA and B are two points on a uniform ring of resistance 15Ω. The <AOB=45∘ The equivalent resistance between A and B is
View SolutionIf you are provided three resistances 2Ω,3Ω and 6Ω. How will you connect then so as to obtain the equivalent resistance of 4Ω ?
View SolutionIf you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
View Solution