What work should be done in order to sqeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the poston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice is s, with s being considerablu less than the piston area. The friction and viscosity are negligibly small. Density of water is ρ
Step by step video & image solution for What work should be done in order to sqeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the poston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice is s, with s being considerablu less than the piston area. The friction and viscosity are negligibly small. Density of water is rho by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - practice Exercise 7.1
10 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Practice Exercise 7.2
8 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
Similar Questions
What work should be done in order to squeeze all water from a horizontally located cylinder (figure) during the time t by means of a constant force acting on the piston? The volume of water in the cylinder is equal to V, the cross-sectional area of the orifice to s, with s being considerably less than the piston area. The friction and viscosity are negligibly small.
View SolutionIf curved surface area of cylinder is equal to its volume. What is the radius of cylinder?
View Solution
Knowledge Check
The magnitude of the volume of a closed right circular cylinder of unit height divided by the magnitude of the total surface area of the cylinder (r being the radius of the cylinder) is equal to
A12(1+1r)B12(1+1r+1)C12(1−1r)D12(1−1r+1)Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
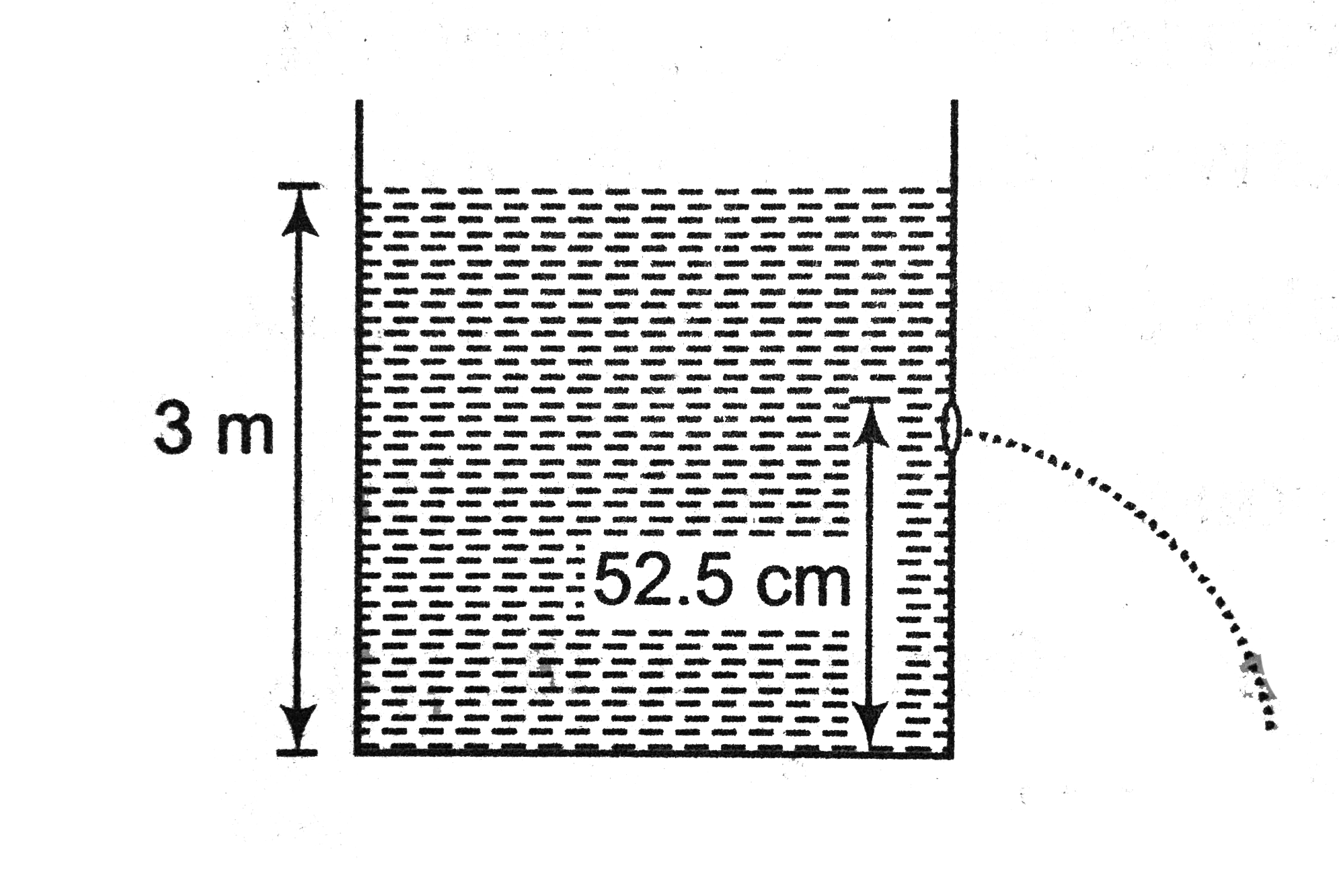A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2Water rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
AhBh/2Ch/4D4h
Suppose you know the area of the base of a cylinder and the height of the cylinder. How can you find the cylinder’s volume?
View SolutionA horizontal cylinder of length l contains water. On the left a constant force F is applied on the piston and on the right there is a small hole of area a. What is the velocity of the piston? Hence, calculate the work done in emptying the vessel in time t. brgt
given area of cylinder is A
View SolutionIf a solid cylinder of area of cross-section A is moving with velocity V in medium of density p then power loss of cylinder is
View SolutionA ideal gas is kept in a cylinder of cross sectional area A and volume v0. The mass of the gas enclosed is M and bulk modulus B. If the piston of the cylinder is pressed by small x, then find the time period of small oscillations,
View SolutionIn a certain gravity free space, the piston of an injection is being pushed so that the water jet comes out with a speed v. The area of the piston is much greater than the orifice of the injection.
View Solution