A vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it, as a result, the rod swings through an angle α. Assuming that m<<M, find:
(a) the velocity of the flying bullet,
(b) the momentum increment in the system "bullet-rod" during the impact, what causes the change of that momentum,
(c) at what distance x from the upper end of the rod the bullet must strike for the momentum of the system "bullet-rod" to remain constant during the impact.
The correct Answer is:⎡⎣Mm√2gl3sinα2,M√gl6sinα2⎤⎦
Step by step video, text & image solution for A vertically oriented uniform rod of mass M and length l can rotate about its upper end. A horizontally flying bullet of mass m strikes the lower end of the rod and gets stuck in it, as a result, the rod swings through an angle alpha. Assuming that m lt lt M, find: (a) the velocity of the flying bullet, (b) the momentum increment in the system "bullet-rod" during the impact, what causes the change of that momentum, (c) at what distance x from the upper end of the rod the bullet must strike for the momentum of the system "bullet-rod" to remain constant during the impact. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:RIGID BODIES AND ROTATIONAL MOTIONExercise:MCQ
Explore 16 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
- WORK, ENERGY AND POWERBook:PHYSICS GALAXY - ASHISH ARORAChapter:WORK, ENERGY AND POWERExercise:unsolved
Explore 1 Video
Similar Questions
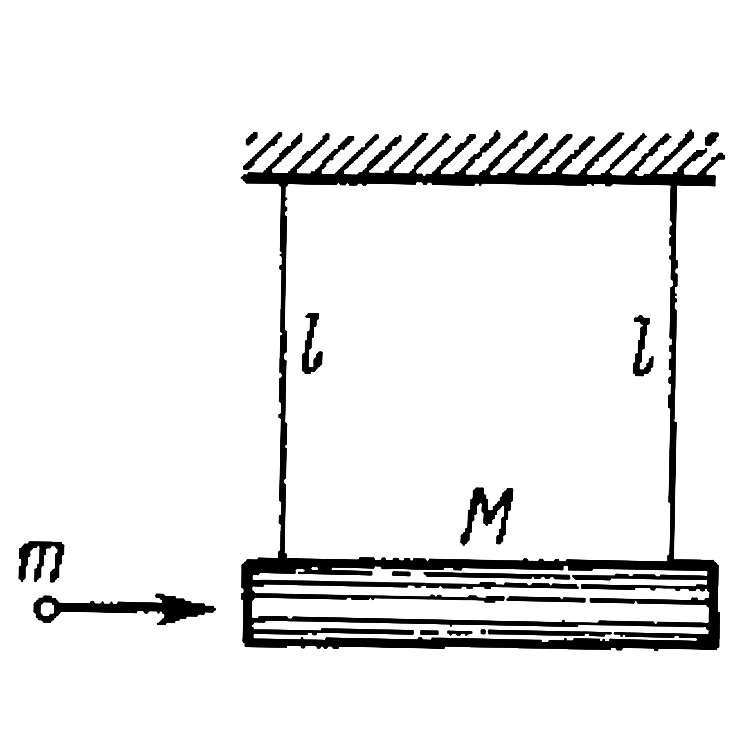
A horizontally flying bullet of mass m gets stuck in a body of mass M suspended by two identical threads of length l (figure).
As a result, the threads swerve through an angle θ. Assuming m<<M, find:
(a) the velocity of the bullet before striking the body,
(b) the fraction of the bullet's initial kinetic energy that turned into heat.
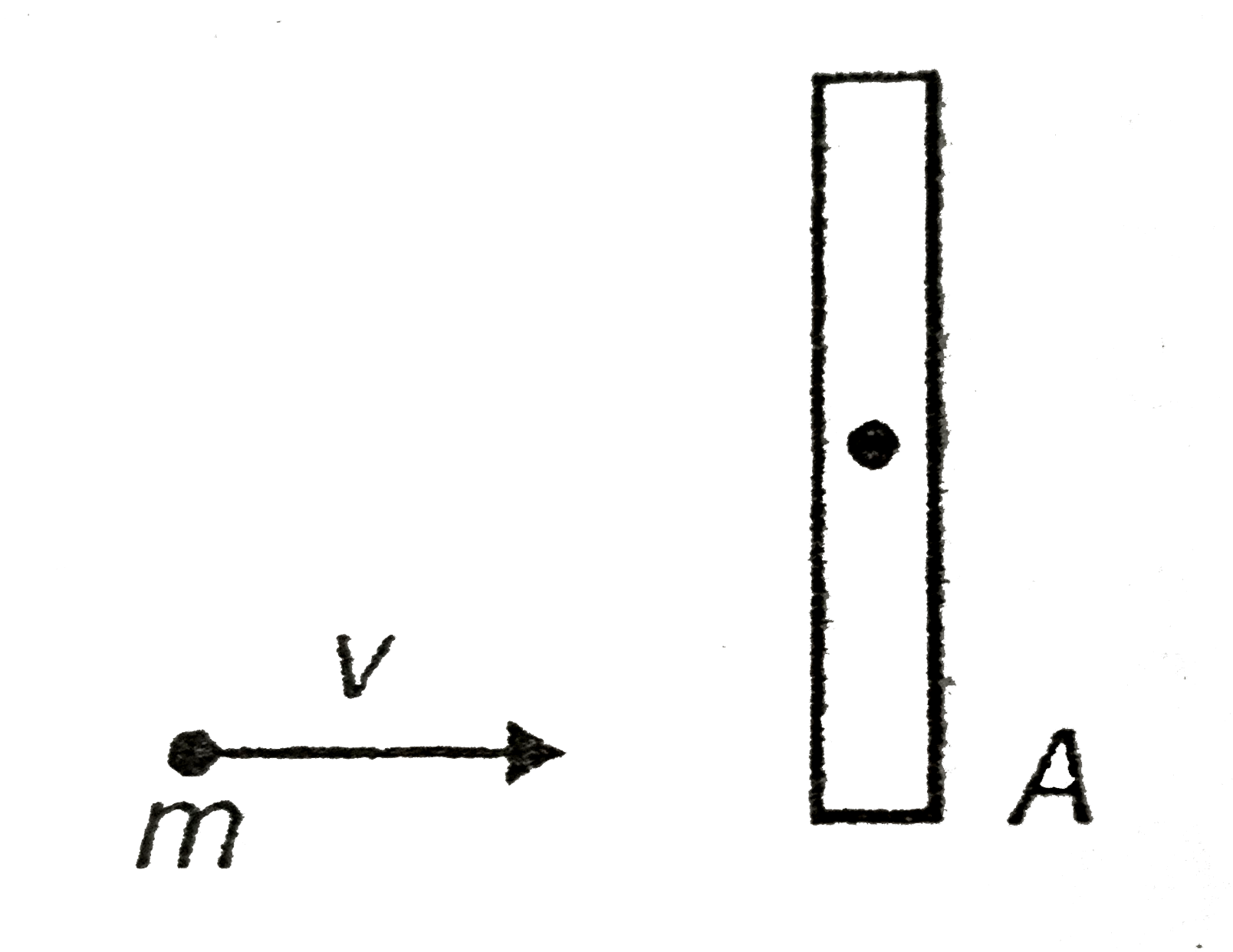
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end. A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
Aml23Bml23sinθCml23sin2θDml23cos2θA uniform rod of mass M is hinged at its upper end. A particle of mass m moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision find the value of M/m?
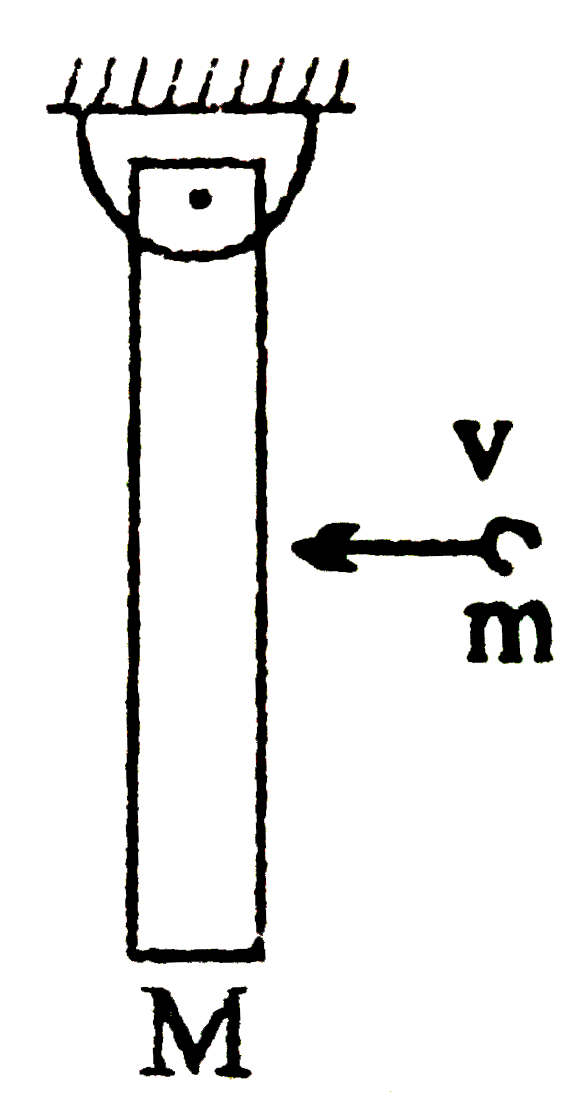 A3/4B4/3C2/3DNone of these
A3/4B4/3C2/3DNone of these

A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
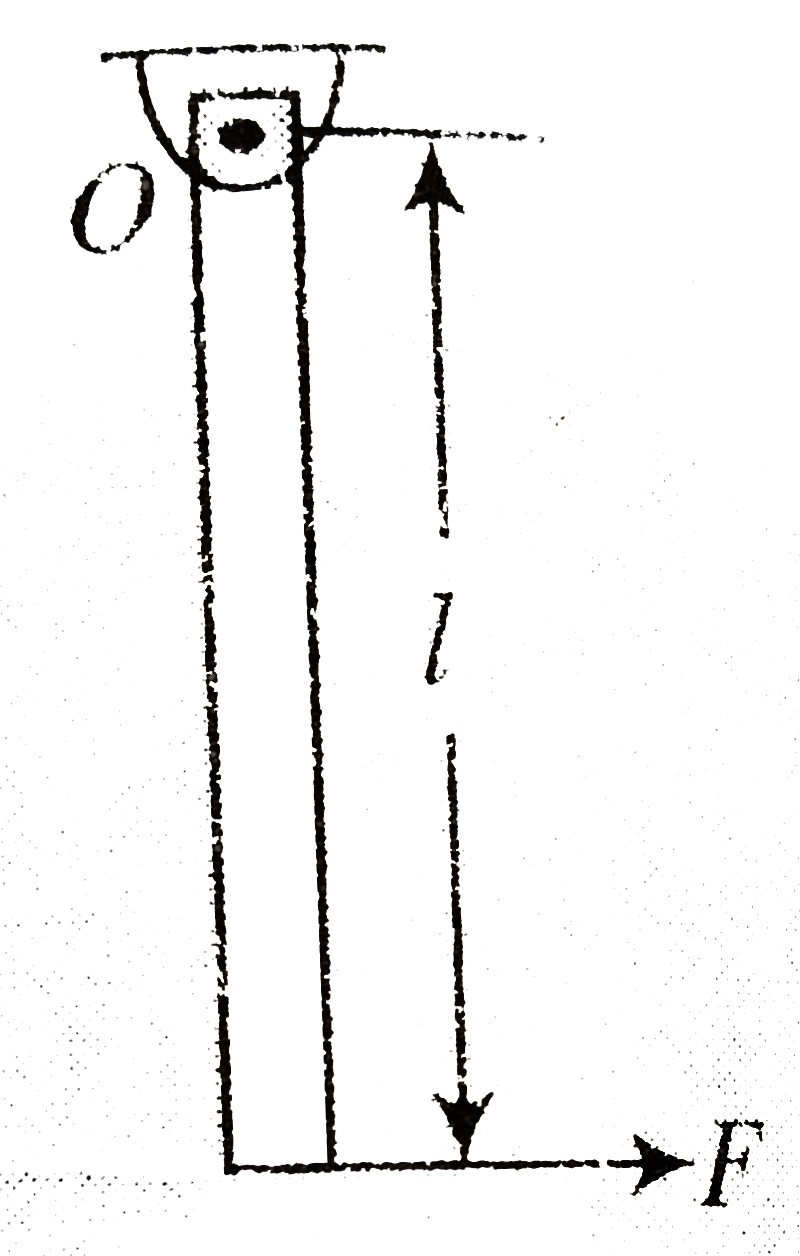
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
View SolutionThe moment of inertia of a thin uniform rod of mass M and length l about an axis perpendicular to the rod through its centre is I. The moment of inertia of the rod through its end point is
View Solution

