Two blocks m1 and m2 are pulled on a smooth horizontal surface, and are joined together with a spring of stiffness k as shown in Fig. Suddenly, block m2 receives a horizontal velocity v0, then the maximum extension xm in the spring is
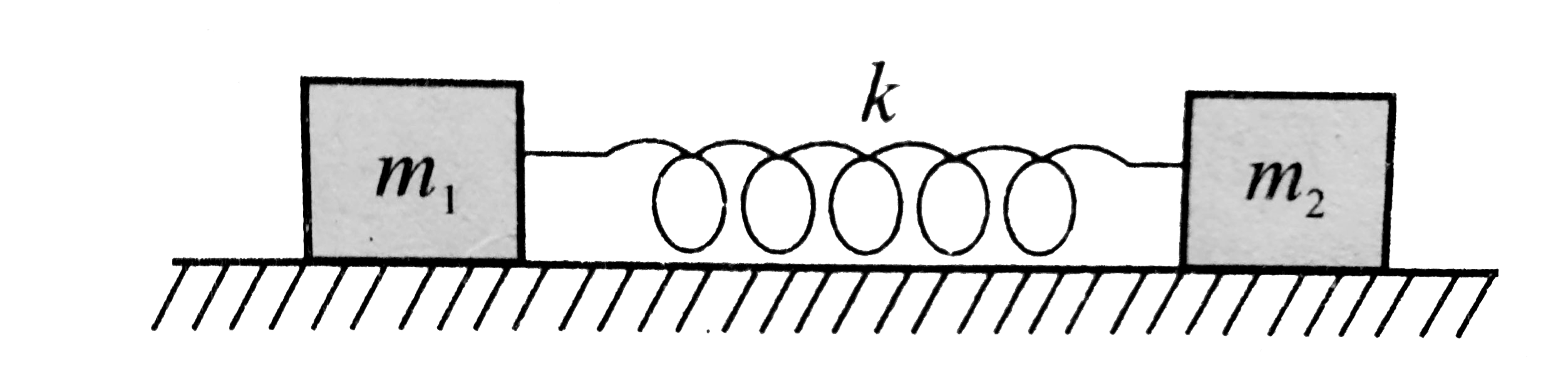
v0√m1m2m1+m2
v0√2m1m2(m1+m2)k
v0√m1m22(m1+m2)k
v0√m1m2(m1+m2)k
The correct Answer is:D
Step by step video, text & image solution for Two blocks m_(1) and m_(2) are pulled on a smooth horizontal surface, and are joined together with a spring of stiffness k as shown in Fig. Suddenly, block m_(2) receives a horizontal velocity v_(0), then the maximum extension x_(m) in the spring is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Advance McQ
Explore 20 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:unsolved
Explore 110 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Conceptual MCQ s single option correct
Explore 30 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
Similar Questions
Two smooth blocks of mases m1andm2 attached with an ideal spring of stiffness k and kept on hrozontal surface. If m1 is projected with a horizontal velocity v0. Find the maximum compression of the spring.
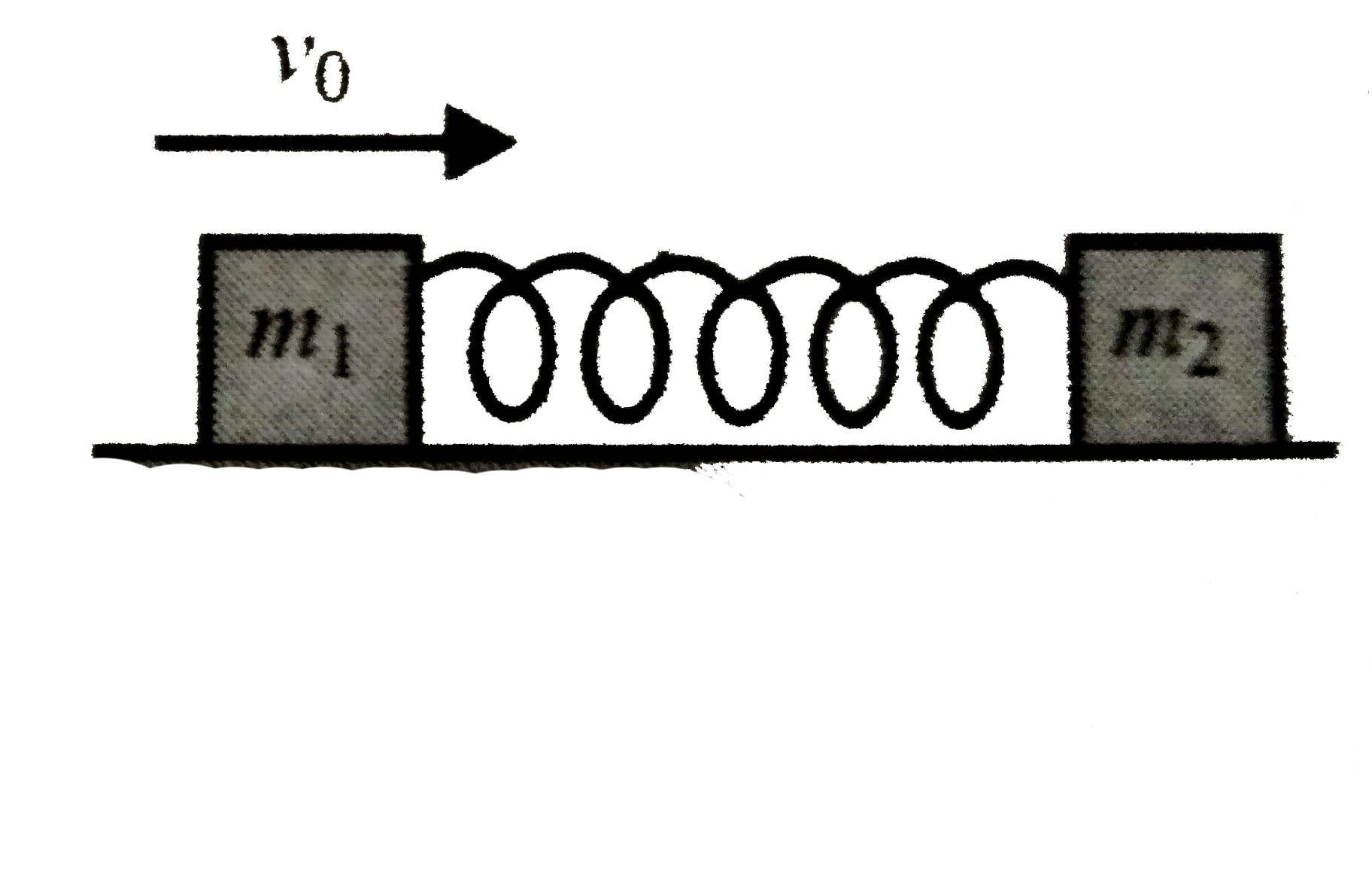
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring
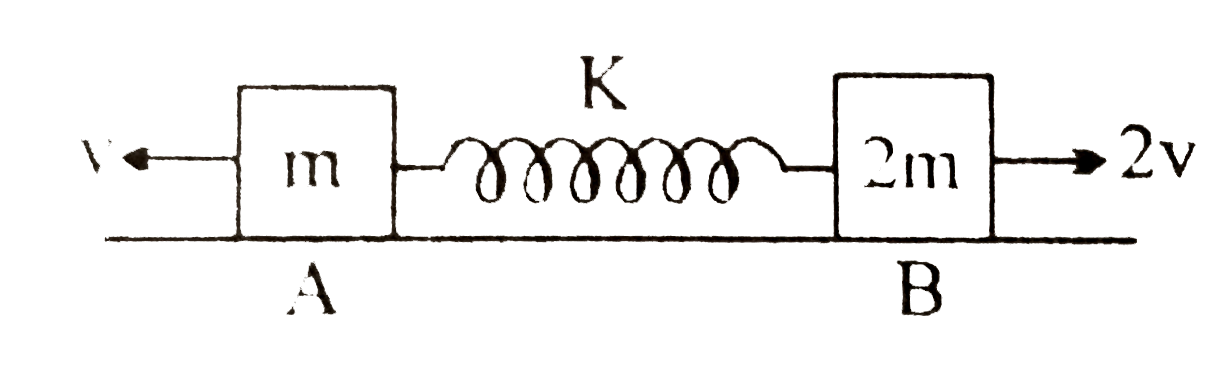
View Solution
Knowledge Check
Two blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
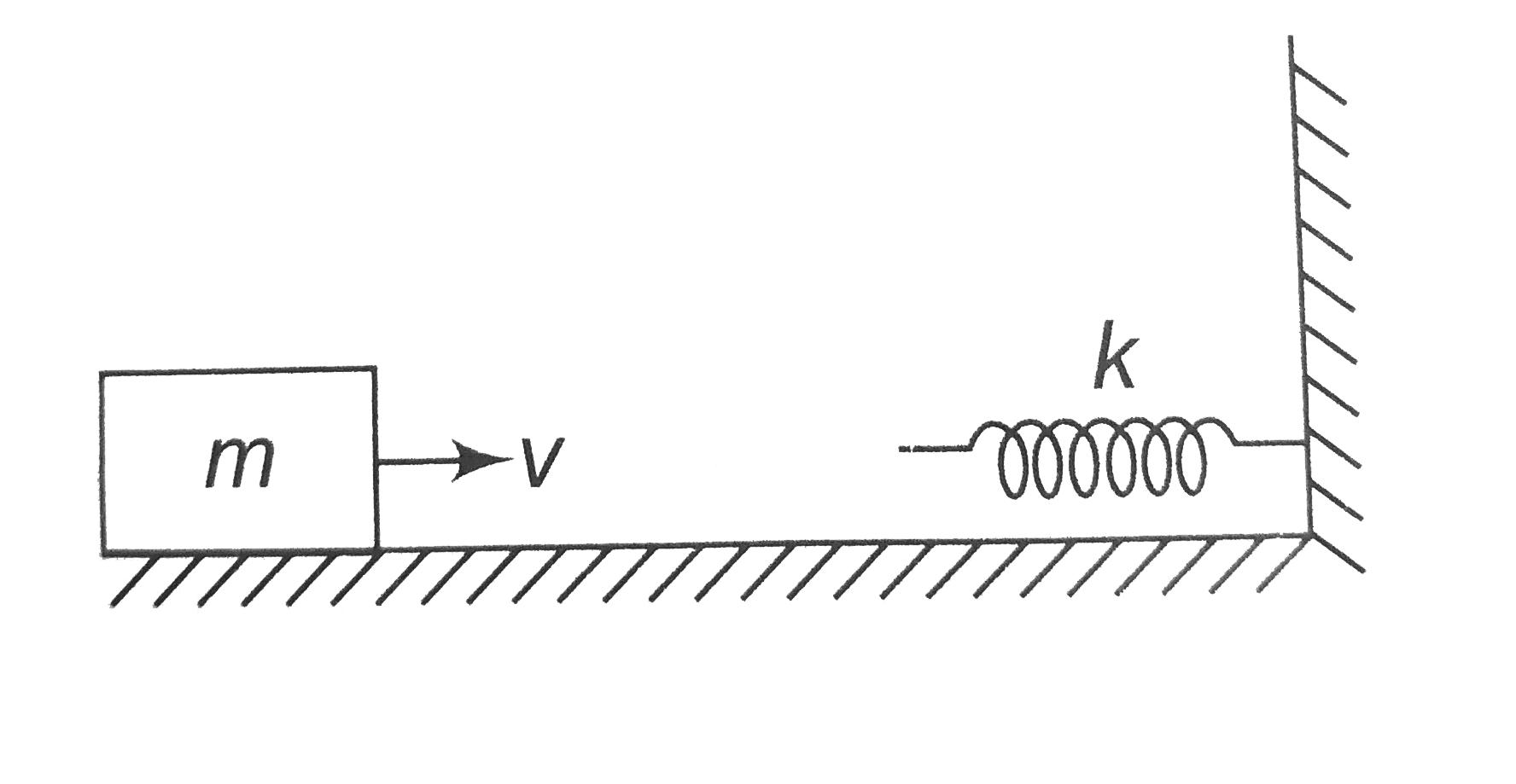
A110B12√10C12√15D0.15A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
Two blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
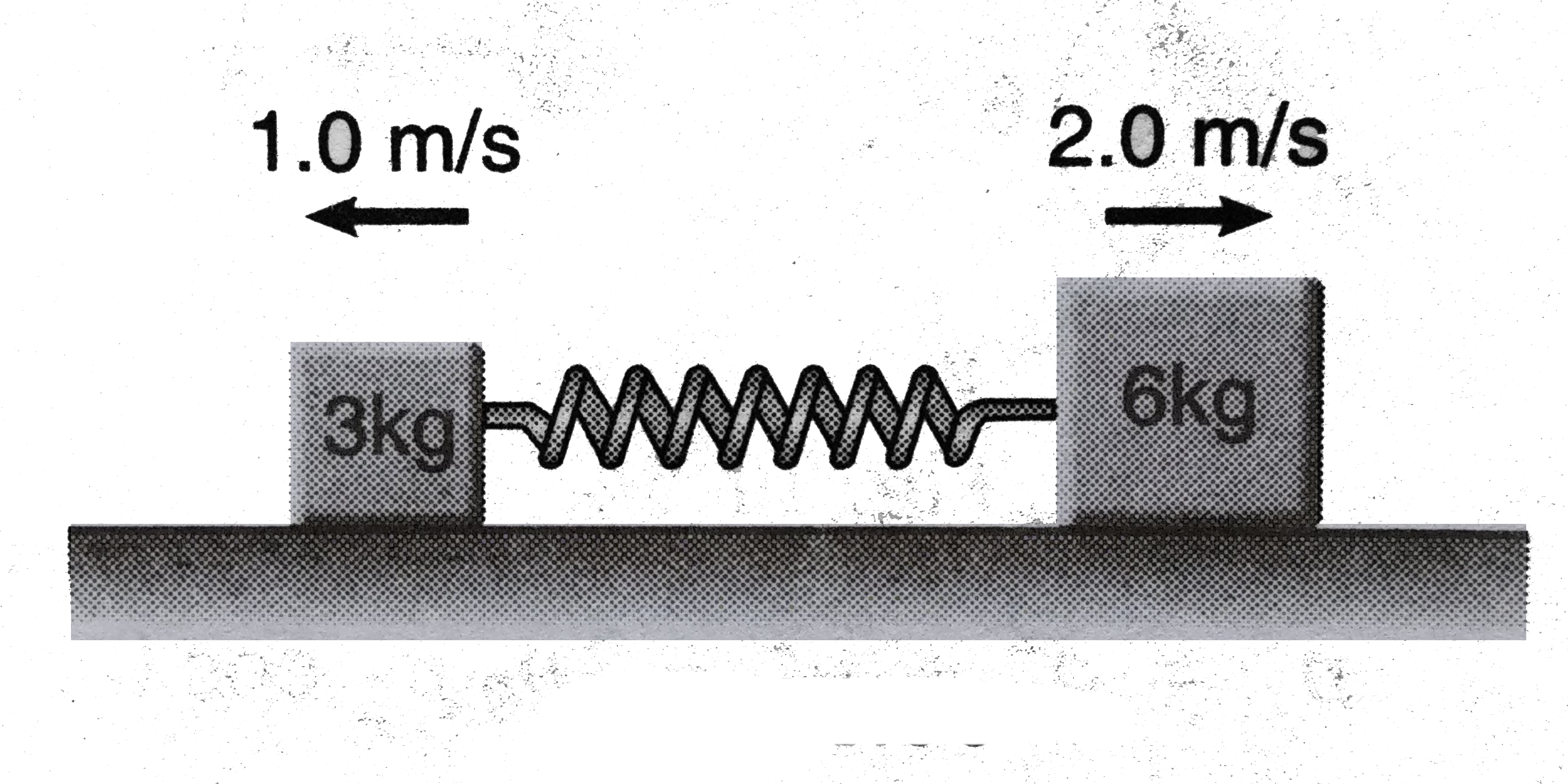
View SolutionTwo blocks A and B of equal mass m=1.0kg are lying on a smooth horizontal surface as shown in figure. A spring of force constant k=200N/m is fixed at one end of block A. Block B collides with block A with velocity v0=2.0m/s. Find the maximum compression of the spring.

View SolutionTwo block of masses m1andm2 are placed side by side on a smooth horizontal surface as shown in fig. A horizontal force F is applied on the block .

(a) Find the acceleration of each block.
(b) Find the normal reaction between the two blocks.
View SolutionThe figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
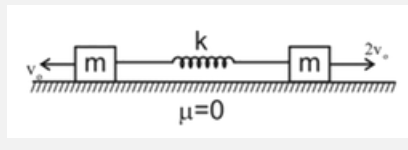
View SolutionA bullted of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial sped of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time forthe bullet - block system to come to rest.
View Solution

