Find centre of mass of an object (Paraboloid) which is formed by rotating a parabola x=ky2 about x-axis and height of object is h as shown in figure. Assume the object is of uniform density.

Step by step video & image solution for Find centre of mass of an object (Paraboloid) which is formed by rotating a parabola x=ky^(2) about x-axis and height of object is h as shown in figure. Assume the object is of uniform density. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Discussio Q
Explore 28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Conceptual MCQ s single option correct
Explore 30 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
Similar Questions
The centre of a mass of any object having uniform density is at its centroid
View SolutionFind out the centre of mass of a composite object shown in figure. Object consists of a cone with its base joint with the base of a hemisphere. The dimensions of the object are shown in figure. Assume uniform density of the system.

View Solution
Knowledge Check
Three particles, each of mass m are placed an the points (x1,y1,z1),(x2,y2,z2) and (x3,y3,z3) on the inner surface of a paraboloid of revolution obtained by rotating the parabola x2=4ay about the y-axis. Neglected the mass of the paraboloid. (y-axis. is along the vertical (a) the moment of inertia of the system about the axis of the paraboloid is I=4ma(y1+y2+y3)
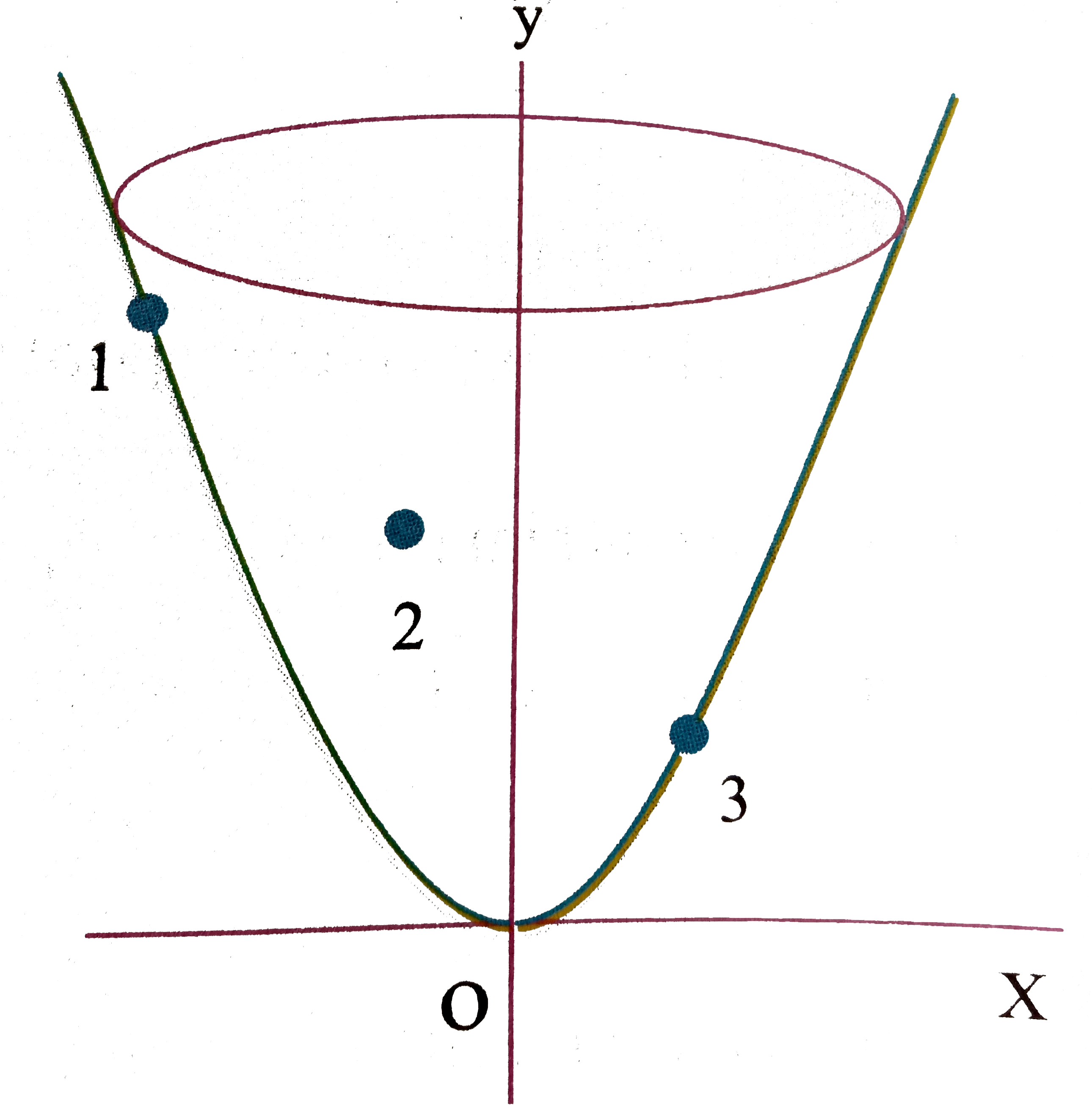 Athe moment of inertia of the system about the axis of the paraboloid is I=4ma(y1+y2+y3)Bif potential energy at O is taken to be zero, the potential energy of the system is mg(y1+y2+y3)Cif the particle at(x1,y1,z1) slides down the smooth surface, its speed at O is √2gy1Dif the parabola spins about OY with an angular speed, ω, the kinetic energy of the system will be 2ma(y1+y2+y3)ω2.
Athe moment of inertia of the system about the axis of the paraboloid is I=4ma(y1+y2+y3)Bif potential energy at O is taken to be zero, the potential energy of the system is mg(y1+y2+y3)Cif the particle at(x1,y1,z1) slides down the smooth surface, its speed at O is √2gy1Dif the parabola spins about OY with an angular speed, ω, the kinetic energy of the system will be 2ma(y1+y2+y3)ω2.Velocity time graph of an object of mass 2kg is shown in figure. The force required to move the object for first four seconds is
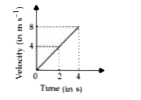 A0NB4NC2ND8N
A0NB4NC2ND8NDisplacement time graph of an object of mass 2kg is shown in figure. The force required to move the object for first four seconds is
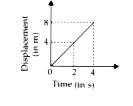 A0B4NC2ND8N
A0B4NC2ND8N
The centre of mass of any object having uniform density. is at its ...............
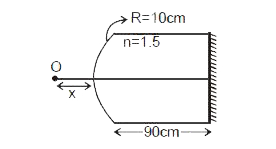
View SolutionFind out the value of x so that the image is formed on the object itself.
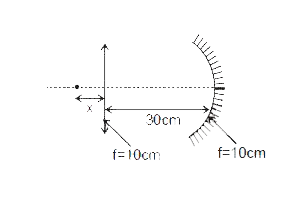
View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
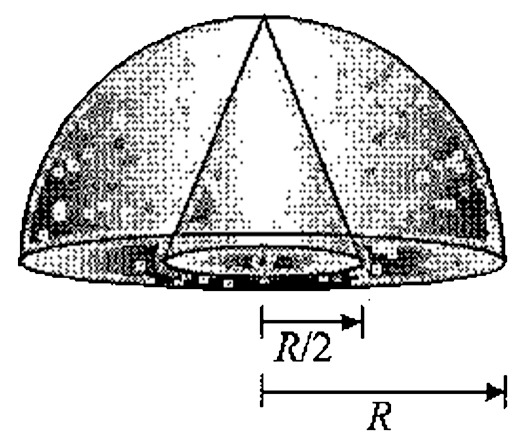
View SolutionFind out the value of x for which the image is formed on the object itself.
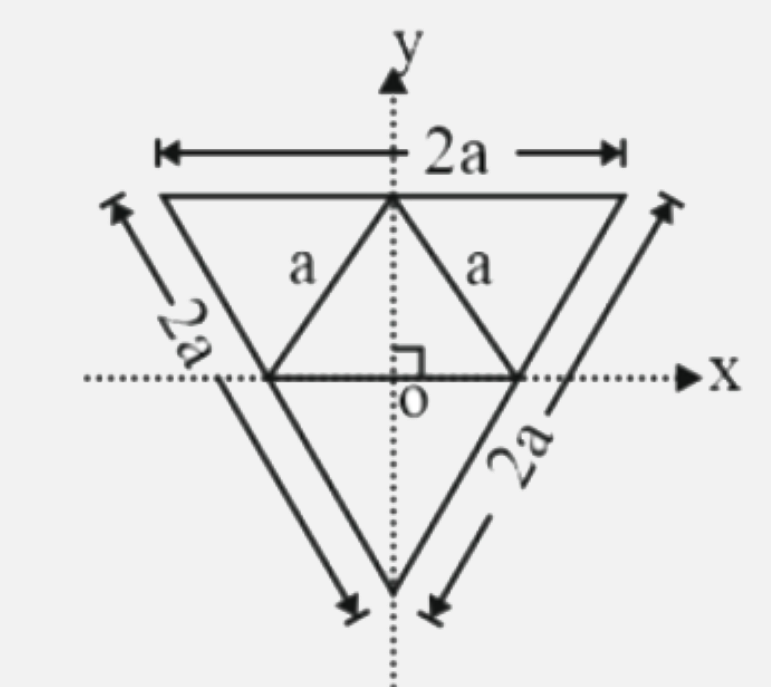
View SolutionThe y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
View Solution

