If the magnetic field at P can be written as Ktan(α2),

A
μ0l4πd
B
μ0I2πd
C
μ0Iπd
D
2μ0lnd
Video Solution
|
Answer
Step by step video & image solution for If the magnetic field at P can be written as K tan (alpha/2), by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:PHYSICS GALAXY - ASHISH ARORAChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:Advance MCQ
Explore 29 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:PHYSICS GALAXY - ASHISH ARORAChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:U.N.P
Explore 79 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:PHYSICS GALAXY - ASHISH ARORAChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:Conceptual MCQ
Explore 37 Videos
- Kinetic Theory of Gases and Gas LawsBook:PHYSICS GALAXY - ASHISH ARORAChapter:Kinetic Theory of Gases and Gas LawsExercise:Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
Explore 64 Videos
- NUCLEAR PHYSICS AND RADIOACTIVITYBook:PHYSICS GALAXY - ASHISH ARORAChapter:NUCLEAR PHYSICS AND RADIOACTIVITYExercise:Concptual MCQs
Explore 48 Videos
Similar Questions
Knowledge Check
A magnetic field can be produced
Aa moving chargeBa changing electric fieldCboth of theseDneither of theseA magnetic field can be produced
Aa moving chargeBa changing electric fieldCboth of theseDneither of theseA magnetic field can be produced by
Aa moving chargeBa changing electric fieldCboth of theseDneither of these
A proton and an α- particle, having kinetic energies KPandKa respectively enter into a magnetic field at right angles. The ratio of the radii of trajectory of proton to that of α− particle is 2:1. The ratio of Kp:Ka is :
View SolutionA magnetic field can be produced by
View SolutionThe magnetic field at centre , P will be
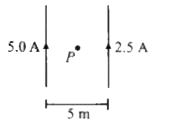
View Solutionp⇒q can also be written as-
View SolutionMetal ring of radius R is placed perpendicular to uniform magnetic field B. Magnetic field starts changing at a rate α
View Solution

