A cylinder of height H and radius R is filled with a liquid of density p . What is the disrupting stress at a heght h? where is it maximum and where minimum ?
[Hint : Disrupting stress is the elastic force per unit length Consider equilibrium of an element of the wall.]
The correct Answer is:
Step by step video, text & image solution for A cylinder of height H and radius R is filled with a liquid of density p . What is the disrupting stress at a heght h? where is it maximum and where minimum ? [Hint : Disrupting stress is the elastic force per unit length Consider equilibrium of an element of the wall.] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View SolutionA large vessel of height H is filled with a liquid of density ρ upto the brim. A small hole of radius r is made at the side vertical face, close to the base. The horizontal force is required to stop the gushing of liquid is
View Solution
Knowledge Check
A cylinder is fill ed with a liquid of density p upto a height h. What is the hydrostatic pressure exerted by the liquid on the bottom of the cylinder, if the cylinder is kept in a lifi moving upwa rds with an acceleration a ?
AρghBρ(g+a)Cρ(g−a)Dρgha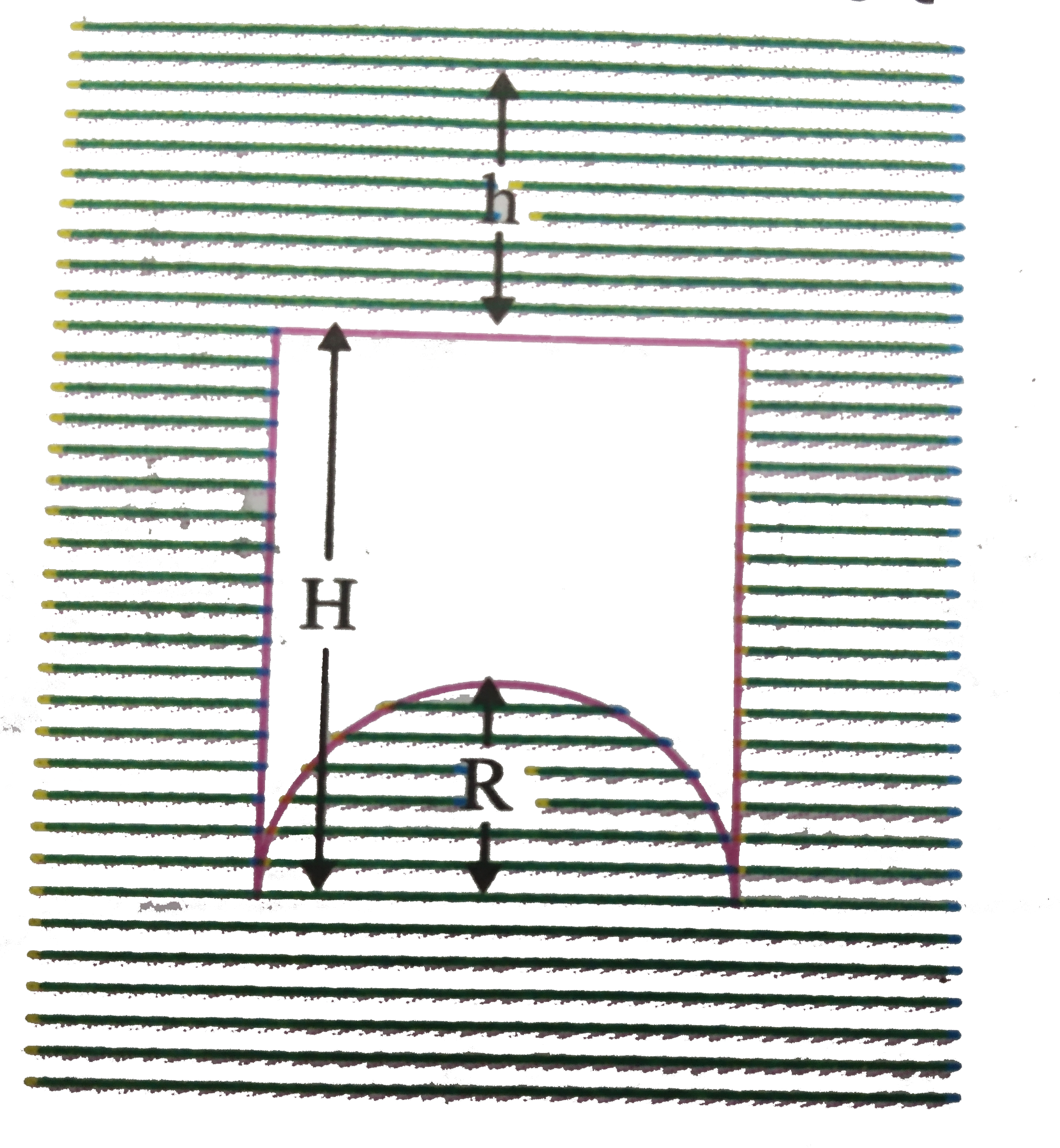
A cylinder of radius R, height H and density simga has a hemispherical cut at its bottom. The top of the cyliner is kept at depth h from the liquid surface. If the density of liquid is ρ, find the hydrostatic force acting on the hemispherical surface of the cylinder.AF2=πR2ρg(H+h−23R)BF2=πR2ρg(H−h+23R)CF2=πR2ρg(H−h−23R)DF2=πR2ρg(H+h+23R)A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32h
A hollow sphere of radius R is filled completely with an ideal liquid of density ρ .Sphere is moving horizontally with an acceleration 2g ,where g is acceleration due to gravity in the space.If minimum pressure of liquid is P0 ,then pressure at the centre of sphere is
View Solution
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)
View SolutionA cylindrical tank has a hole of diameter 2r in its bottom. The hole is covered wooden cylindrical block of diameter 4r, height h and density ρ/3.

Situation I: Initially, the tank is filled with water of density ρ to a height such that the height of water above the top of the block is h1 (measured from the top of the block).
Situation II: The water is removed from the tank to a height h2 (measured from the bottom of the block), as shown in the figure. The height h2 is smaller than h (height of the block) and thus the block is exposed to the atmosphere.
Find the height of the water level h2 (in situation 2), for which the block remains in its origin) position whithout the application of any external force
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

Time period of vertical S.H.M of the cylinder is
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

If the cyleinder is displced by a small downward displacement a from its equilibrium postion and then released , the restoring force on it will be
View Solution

