an oil tanker moving with speed v decelerates uniformly and comes to a stop within a distance s . Find the pressure due to the oil to the back and front walll of the tanker during the period of deceleration. Assume the taker to be a parallelpiped of length l, width b and heigth lt and the density of the oil to be p.
The correct Answer is:F1=12pbh(gh+v2l4s)andF2=12pbh(gh−V2l4s)
Step by step video, text & image solution for an oil tanker moving with speed v decelerates uniformly and comes to a stop within a distance s . Find the pressure due to the oil to the back and front walll of the tanker during the period of deceleration. Assume the taker to be a parallelpiped of length l, width b and heigth lt and the density of the oil to be p. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
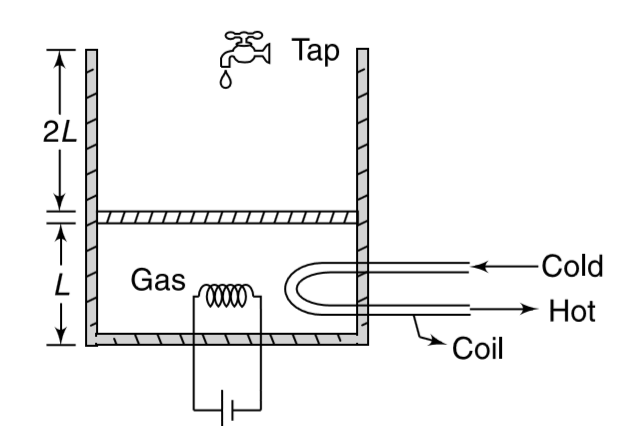
A cylindrical container of height 3L and cross sectional area A is fitted with a smooth movable piston of negligible weight. It contains an ideal diatomic gas. Under normal atmospheric pressure P0 the piston stays in equilibrium at a height L above the base of the container. The gas chamber is provided with a heater and a copper coil through which a cold liquid can be circulated to extract heat from the gas. Volume occupied by the heater and the liquid coil is negligible. Following set of operations are performed to take the gas through a cyclic process.
(1) Heater is switched on. At the same time a tap above the cylinder is opened. Water fills slowly in the container above the piston and it is observed that the piston does not move. Water is allowed to fill the container so that the height of water column becomes L. Now the tap is closed.
(2) The heater is kept on and the piston slowly moves up. Heater is switched off at the time water is at brink of overflowing.
(3) Now the cold liquid is allowed to pass through the coil. The liquid extracts heat from the gas. Water is removed from the container so as to keep the position of piston fixed. Entire water is removed and the gas is brought back to atmospheric pressure.
(4) The circulation of cold liquid is continued and the piston slowly falls down to the original height L above the base of the container. Circulation of liquid is stopped. Assume that the container is made of adiabatic wall and density of water is ρ. Force on piston due to impact of falling water may be neglected.
(a) Draw the entire cycle on a P–V graph.
(b) Find the amount of heat supplied by the heater and the amount of heat extracted by the cold liquid from the gas during the complete cycle.
View SolutionA train with cross - sectional are St is moving with speed vi inside a long tunnel cross - sectional area S0(S0−4Sl). Assme that almost all the air (density ρ) in front of the train back between its sides and the wall of the tunel. Also the air flow with respect to the train is steady and laminar . Take the ambient pressure and that inside the train to be p0. If the pressure in the region between the sides of the train and the tunnel wall is p , then p0−p=72Nρv2t .Then value of N is ________
View Solution
Knowledge Check
A train of length L move with a constant speed Vt. A person at the back of the train fires a bullet at time t = 0 towards a target which is at a distance of D ( at time t = 0 ) from the front of the train ( on the same direction of motion ). Another person at the front of the train fires another bullet at time t = T towards the same target. Both bullets reach the target at the same time. Assuming the speed of the bullets Vb are same, the length of the train is
AT(Vb×2Vt)BT(Vb+Vt)C2T(Vb+2Vt)D2T(Vb−2Vt)A uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
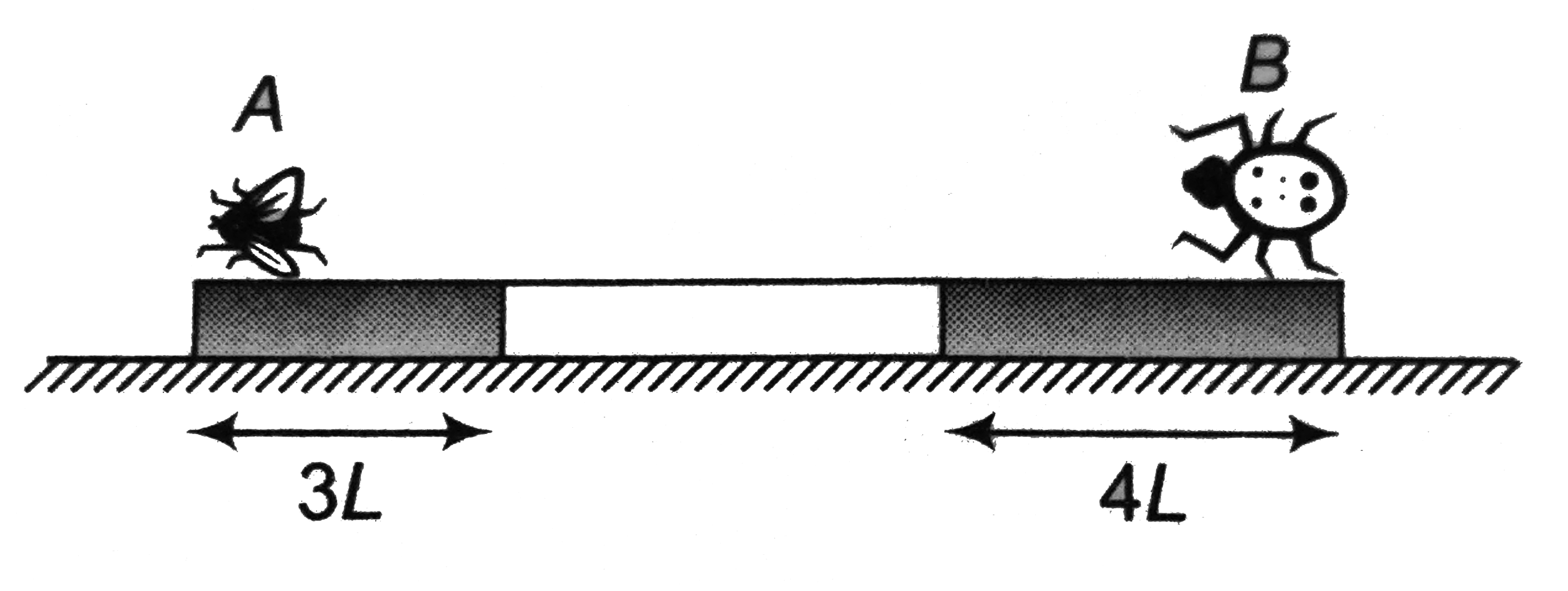
By what distance the centre of mass of the rod shifts during this time?A(a) 8L3B(b) 4L3C(c) LD(d) L3Ram and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1A(a) 1920B(b) 1910C(c) 1019D(d) 2019
A conducting bar of mass m length l is pushed with a speed V0 on a smooth horizontal conducting rail containing an inductance L. If the applied magnetic field has inward field induction B find the maximum distance covered by the bar before it stops. Assume that the induced current i=0 when the bar is at the position of the inductor .
(##FIITJEE_PHY_MB_05_C02_SLV_018_Q01.png" width="80%">
View SolutionA uniform board of length L is sliding along a smooth (frictionless) horizontal plane as in figure. The board then slides across the boundary with a rough horizontal surface. The coefficient of kinetic friction between the board and the second surface surface is μk

a. Find the acceleration of the board at the moment its front end has traveled a distance x beyond the boundary.
b. The board stops at the moment its back end reaches the boundary, as in figure. Find the initail speed v of the board.
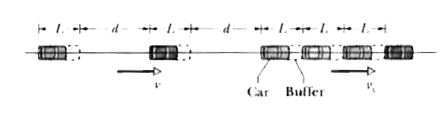
View SolutionTraffic shock wave. An abrupt shlowdown in concentrated traffic can travel as a pulse, termed a shock wave, along the line of cars, either downstream ( in the traffic direction) or upstream, or it can be stationary. Figure 2-17 shows a uniformly spaced line of cars moving at speed v=25.0 m/s toward a uniformly spaced line of slow cars moving at speed vs=5.00 m/s. Assume that each faster car adds length L=12.0 m (car length plus buffer zone ) to the line of slow cars when it joins the line, and assume it slows abruptly at the last instant. (a) For what separation distance d between the faster cars does the shock wave remain stationary ? It the separation is twice that amount, what are the (b) speed and (c) direction ( upstream or downstream ) of the shock wave ?
View SolutionA string of linear mass density 0.5gcm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end. The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20cms−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to regain its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string ?

View SolutionThin films, including soap bubbles and oil show patterns of alternative dark and bright regions resulting from interference among the reflected ligth waves. If two waves are in phase, their crests and troughs will coincide. The interference will be cosntructive and the amlitude of resultant wave will be greater then either of constituent waves. If the two wave are not of phase by half a wavelength (180∘), the crests of one wave will coincide width the troughs of the other wave. The interference will be destructive and the ampliutde of the resultant wave will be less than that of either consituent wave.
1. When incident light I, reaches the surface at point a, some of the ligth is reflected as ray Ra and some is refracted following the path ab to the back of the film.
2. At point b, some of the light is refracted out of the film and part is reflected back through the film along path bc. At point c, some of the light is reflected back into the film and part is reflected out of the film as ray Rc.
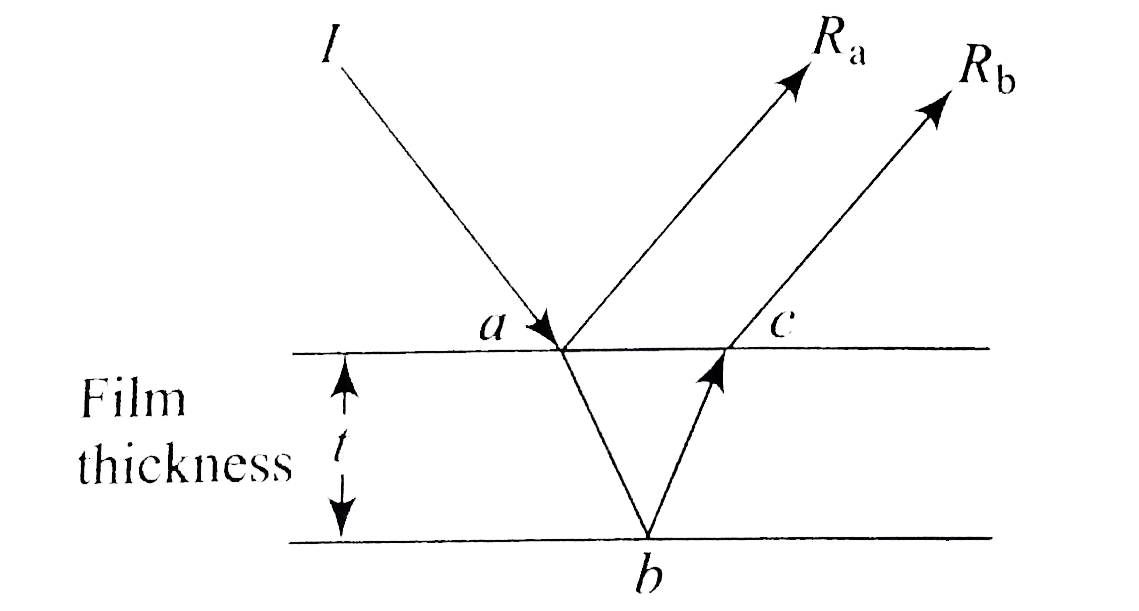
Ra and Rc are parallel. However, Rc has travelled the extra distance within the film fo abc. If the angle of incidence is small, then abc is approxmately twice the film's thickness .
If Ra and Rc are in phase, they will undergo constructive interference and the region ac will be bright. If Ra and Rc are out of phase, they will undergo destructive interference and the region ac will be dark.
I. Refraction at an interface never changes the phase of the wave.
II. For reflection at the interfere between two media 1 and 2, if n1>n2, the reflected wave will change phase. If n1<n2, the reflected wave will not undergo a phase change.
For reference, nair=1.00.

III. If the waves are in phase after reflection at all intensities, then the effects of path length in the film are:
Constrictive interference occurs when 2t=mλ/n,m=0,1,2,3,...
Destrcutive interference occurs when 2t=(m+12)λn,
m=0,1,2,3,...
If the waves are 180∘ out of the phase after reflection at all interference, then the effects of path length in the film ara:
Constructive interference occurs when
2t=(m+12)λn,m=0,1,2,3,...
Destructive interference occurs when
2t=mλn,m=0,1,2,3,...
72. A film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View Solution

