A ball moving translationally collides elastically with another, stationary, ball of the same mass. At the moment of impact the angle between the straight line passing through the centres of the balls and the direction of the initial motion of the striking ball is equal to α=45∘. Assuming the balls to be smooth, find the fraction η of the kinetic energy of the striking ball that turned into potential energy at the moment of the maximum deformation.
The correct Answer is:η=12cos2α
Step by step video, text & image solution for A ball moving translationally collides elastically with another, stationary, ball of the same mass. At the moment of impact the angle between the straight line passing through the centres of the balls and the direction of the initial motion of the striking ball is equal to alpha=45^@. Assuming the balls to be smooth, find the fraction eta of the kinetic energy of the striking ball that turned into potential energy at the moment of the maximum deformation. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTION, FREE BODY DIAGRAMBook:NN GHOSHChapter:LAWS OF MOTION, FREE BODY DIAGRAMExercise:Exercise (A)
Explore 27 Videos
- KINETIC THEORY OF GASESBook:NN GHOSHChapter:KINETIC THEORY OF GASESExercise:All Questions
Explore 24 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBook:NN GHOSHChapter:MOMENT, TORQUE, EQUILIBRIUM OF BODIESExercise:Exercises
Explore 33 Videos
Similar Questions
A ball moving along a straight line collides elastically with another stationary ball of the same mass. At the moment of collision, the angle between the straight line passing through the centres of the balls and the direction of tr initial motion of the striking ball is θ, find the fraction of the kinetic energy of the striking ball converted into potential energy at the moment of the maximum deformation.
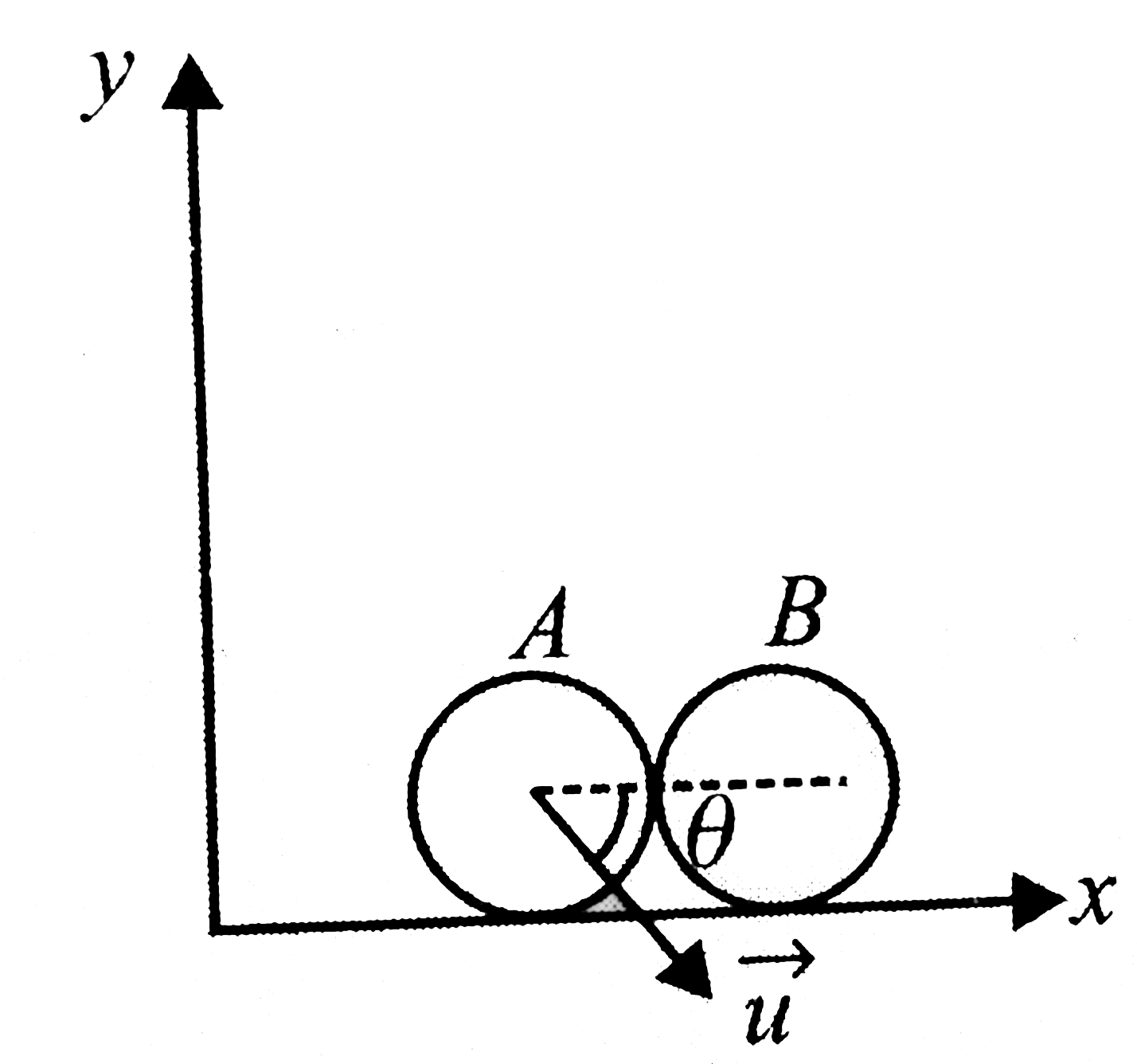
View SolutionA ball of mass M collides elastically with another stationary ball of mass m. If M>m, find the maximum angle of deflection of M.
View Solution
Knowledge Check
A ball of mass M moving with speed v collides perfectly inelastically with another ball of mass m at rest. The magnitude of impulse imparted to the first ball is
AMvBmvCMmM+mvDM2M+mvA ball of mass 'm', moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
AmB2mC4mDinfinityA ball of mass 'm', moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
AmB2 mC4 mDInfinity
Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
View SolutionConsider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is
View Solution

