In the previous question let V0 be the volume of each container. All other details remain the same. The number of moles of gas in the container at temperature 2T0 will be
p0V02RT0
p0V0RT0
2p0V03RT0
p0V03RT0
Step by step video & image solution for In the previous question let V_(0) be the volume of each container. All other details remain the same. The number of moles of gas in the container at temperature 2 T_(0) will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Equal volume of all gases always contains equal number of moles.
View SolutionTwo containers are filled with ideal gases at the same temperature. In the container on the left is a gas of molar mass 2M, volume 2V, and number of moles ⋅2n. In the container on the right is a gas of molar mass M, voluine V, arid moles n. The ratio of the pressure of the gas on the left to- the pressure of the gas on the right container is
'(##CEN_KSR_PHY_JEE_C13_E01_024_Q06##)'
View Solution
Knowledge Check
In the previous questions, if the mass of the body is half the mass of the earth, and all other data remain the same, then t is equal to
A√2H/gB√H/gC√2H/3gD√4H/3gTwo identical container each of volume V0 are joined by a small pipe. The containers contain identical gases at temperature T0 and pressure P0. One container is heated to temperature 2T0 while maintaining the other at the same temperature. The common pressure of the gas is P and n is the number of moles of gas in container at temperature 2T0.
AP=2P0BP=43P0Cn=2P0V03RT0Dn=2P0V02RT0Two cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)

If work done by gas in cylinder B is WB & work done by gas in cylinder A is WA thenAWA=−WBB|WA|>|WB|C|WA|<|WB|Dwe can't say anything
Two cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5)

The mass of gas in cylinder B
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas=1.5)
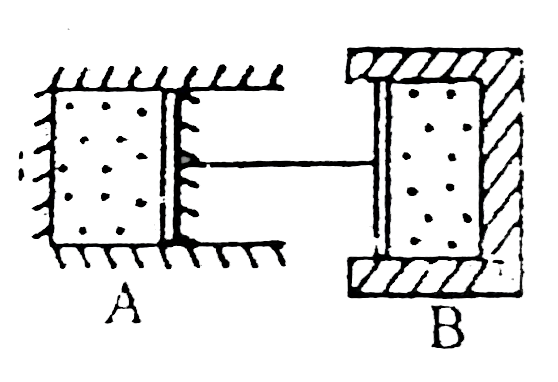
The change in internal energy of gas in cylinder A
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)
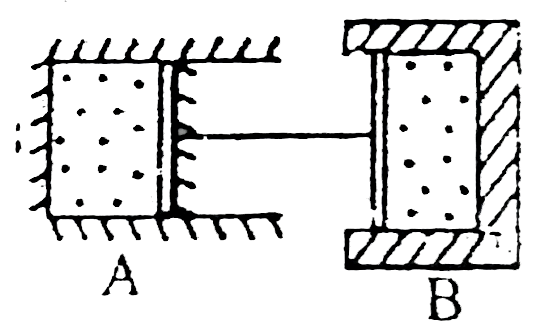
What will be the compressive force in conneting rod at equilibrium
View SolutionAn ideal gas has pressure p0 in container of volume V0.The number of molecules of the gas is doubled without changing the temperature. What is the new value of pressure times volume?
View SolutionThe equation of state for a gas is given by PV=ηRT+αV, where η is the number of moles and α a positive constant. The intinal pressure and temperature of 1 mol of the gas contained in a cylinder is P0 and T0, respectively. The work done by the gas when its temperature doubles isobarically will be
View Solution

