A ball strikes a wall with a velocity →u at an angle θ with the normal to the wall surface. and rebounds from it at an angle β with the surface. Then
(θ+β) is never less than 90∘ if wall is smooth
If wall is smooth coefficient of restitution =tanβcotθ
If wall is smooth coefficient of restitution <tanβtanθ
None of these
Step by step video & image solution for A ball strikes a wall with a velocity vecu at an angle theta with the normal to the wall surface. and rebounds from it at an angle beta with the surface. Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:L-3,(P-1)
Explore 5 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:P-2
Explore 9 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:Level 1
Explore 110 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- RIGID BODY MOTIONBook:ANURAG MISHRAChapter:RIGID BODY MOTIONExercise:MATCH THE COLUMN
Explore 12 Videos
Similar Questions
A ball strikes a smooth horizontal floor at an angle α with the normal to the surface and after rebounding from the floor , ball moves at an angle β with the normal . Find the relation between α and β if coefficient of elasticity is e .
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View Solution
Knowledge Check
A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60∘ with the wall and reflects at the same angle. If it remains in contact with wall for 0.1 s, then the force is
A0B10√3 NC30√3ND40√3NA ball is projected at t=0 with velocity v0 at angle θ with horizontal. It strikes a smooth wall at a distance from it and then falls at a distance d from the wall. Coefficient of restitution is 'e' then :
ABall will return to ground at t=2v0sinθgBd=e(R−L)(whereRisv0sin2θg)Cmaximum height during motion =v20sin2θ2gDit will return to ground at t<2v0sinθgA ball moving with velocity u strikes a smooth horizontal floor at an angle α with the normal to the surface at the point of contact . After collision , ball moves with velocity v at an angle β with the normal . Assume e as the coefficient of restitution .
Atanα=etanβBImpulse applied by the surface on the ball is mu(1+e)cosCv=u√(sin2α+e2cos2α)Dv=tanα
A 1 kg particle strikes a wall with velocity 1 m/s at an angle of 60o with the wall and reflects at the same angle. If it remains in contact with the wall for 0.1 s, then the force is
View SolutionA 1kg particle strikes a wall with a velocity 1ms at an angle of 60°with the wall and reflects at the same angle.If it remains in contact with the wall for 0.1sec, then the force is
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
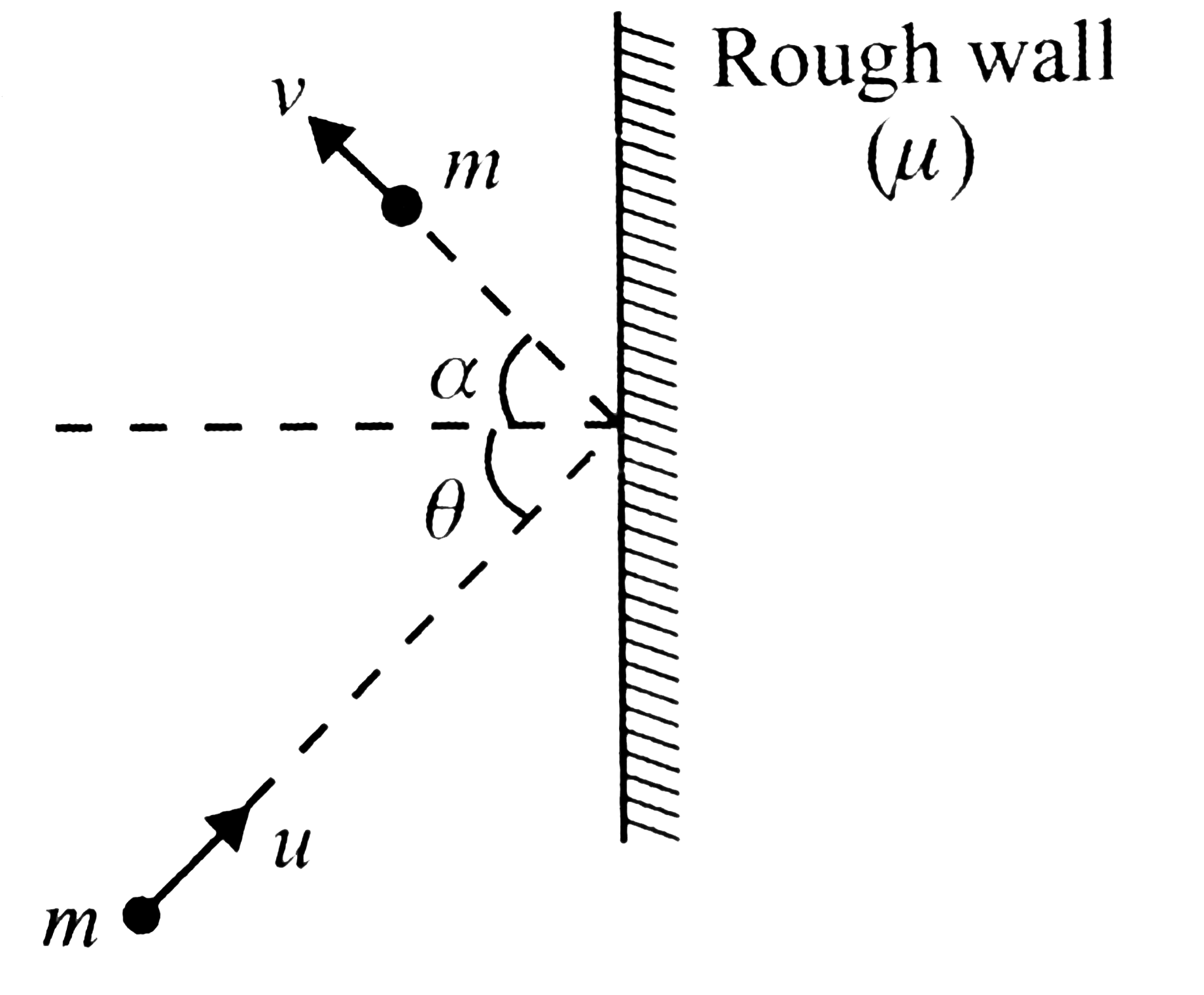
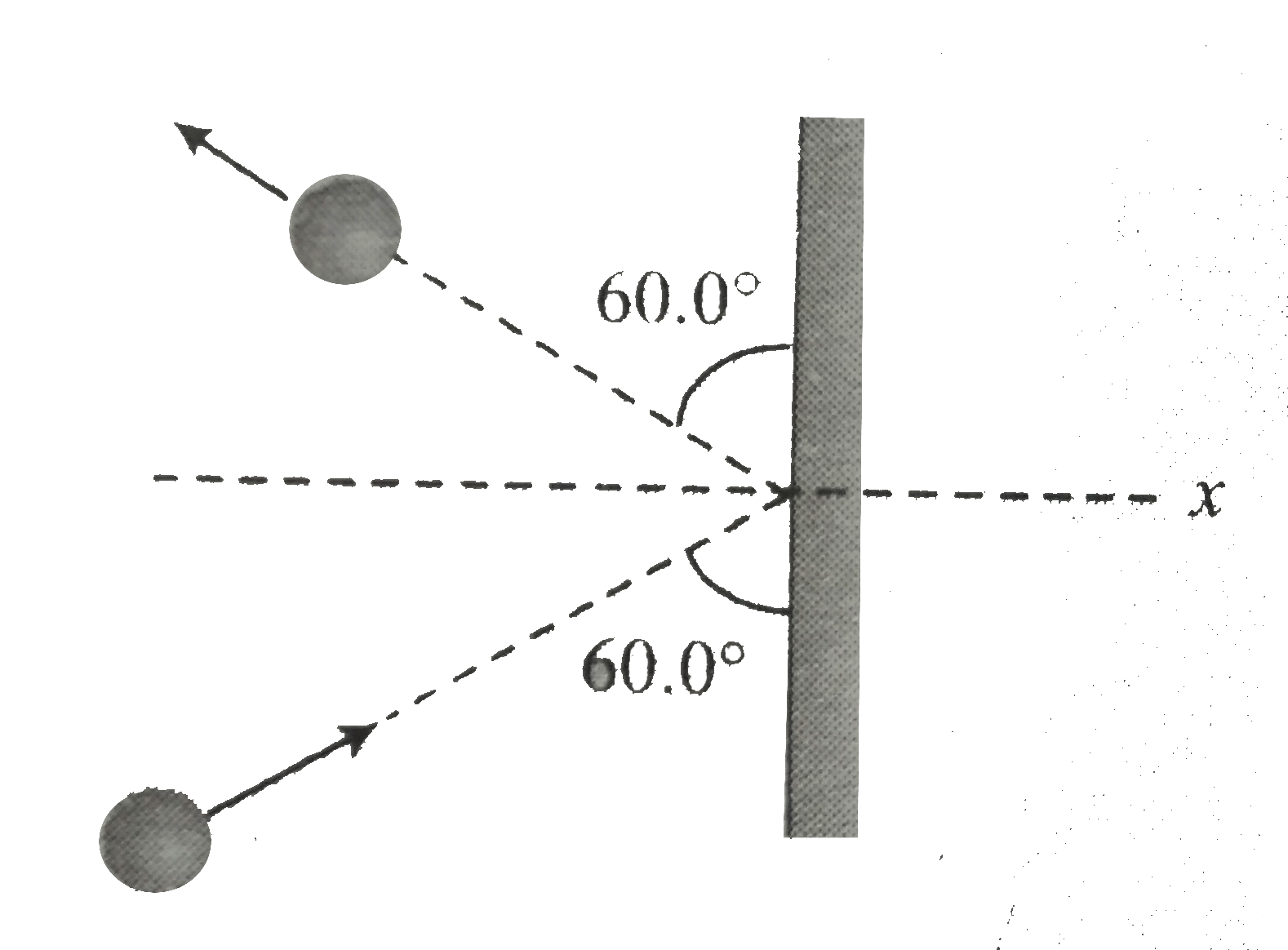
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
View SolutionA ray of light strikes a glass slab at an angle of 50∘ with the normal to the surface of the slab. What is the angle of incidence?
View Solution

