Two identical balls A and B lie on a smooth horizontal surface, which gradually merges into a curve to a height 3.2m. Ball A is given a velocity of 10m/s, to collide head-on with ball B, which then takes up the curved path. What is the minimum coefficient of restitution, e, for the collision between A and B in order that ball B reaches the highest point C of the curve.

12
35
14
34
The correct Answer is:B
Step by step video, text & image solution for Two identical balls A and B lie on a smooth horizontal surface, which gradually merges into a curve to a height 3.2 m. Ball A is given a velocity of 10 m//s, to collide head-on with ball B, which then takes up the curved path. What is the minimum coefficient of restitution, e, for the collision between A and B in order that ball B reaches the highest point C of the curve. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:L-2
Explore 21 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:L-3,(P-1)
Explore 5 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:Example
Explore 50 Videos
- FORCE ANALYSISBook:ANURAG MISHRAChapter:FORCE ANALYSISExercise:Matching type
Explore 13 Videos
- RIGID BODY MOTIONBook:ANURAG MISHRAChapter:RIGID BODY MOTIONExercise:MATCH THE COLUMN
Explore 12 Videos
Similar Questions
A ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View SolutionTwo identical balls, of equal masses A and B, are lying on a smooth surface as shown in Fig. Ball A hits ball B (which is at rest) with a velocity v=16m/s. What should be the minimum value of coefficient of restitution between A and B so that B just reaches the highest point of inclined plane?

View Solution
Knowledge Check
A 2kg ball , moving at 10m/s , collides head - on with a 3kg ball moving in the opposite direction at 20m/s. If the coefficient of restitution is 1/3 , then the energy lost in the collision is
A120JB240JC360JD480JA ball moving with velocity 2ms−1 collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms−1) after collision will be
A0,1B1,1C1,0.5D0,2A ball moving with velocity 2 m/s collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in m/s) after collision will be
A0,1B1,1C1, 0.5D0,2
A ball of mass moving with a velocity u collides head on with a ball B of mass m at rest. If the coefficient of restitution is e. the ratio of final velocity of B to the initial velocity of A is
View SolutionTwo identical balls of equal masses A and B, are lying on a smooth surface as shown in the figure. Ball A hits the ball B (which is at rest) with a velocity v=16ms−1. What should be the minimum value of coefficient of restitution e between A and B so that B just reaches the highest point of inclined plane? (g=10ms−2)

View SolutionN identical balls are placed on a smooth horizontal surface. An another ball of same mass collides elastically with velocity u with first ball of N balls. A process of collision is thus started in which first ball collides with second ball and the with the third ball and so on. The coefficient of restitution for each collision is e. Find the speed of Nth ball.
View SolutionA ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
View SolutionTwo identical balls of equal masses A and B , are lying on a smooth surface as shown in figure Ball A hits the ball B (which is at rest) with a velocity v=16m/s What should be the minimum value of coefficient of restitution e beteeen A and B so that B just reaches the highest point of inclined plane:
(Takeg=10m/s2)
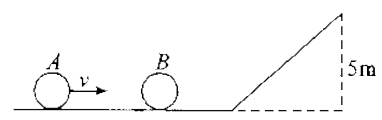
View Solution

