A swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angleθ with the perpendicular as shown ip. the. figure.
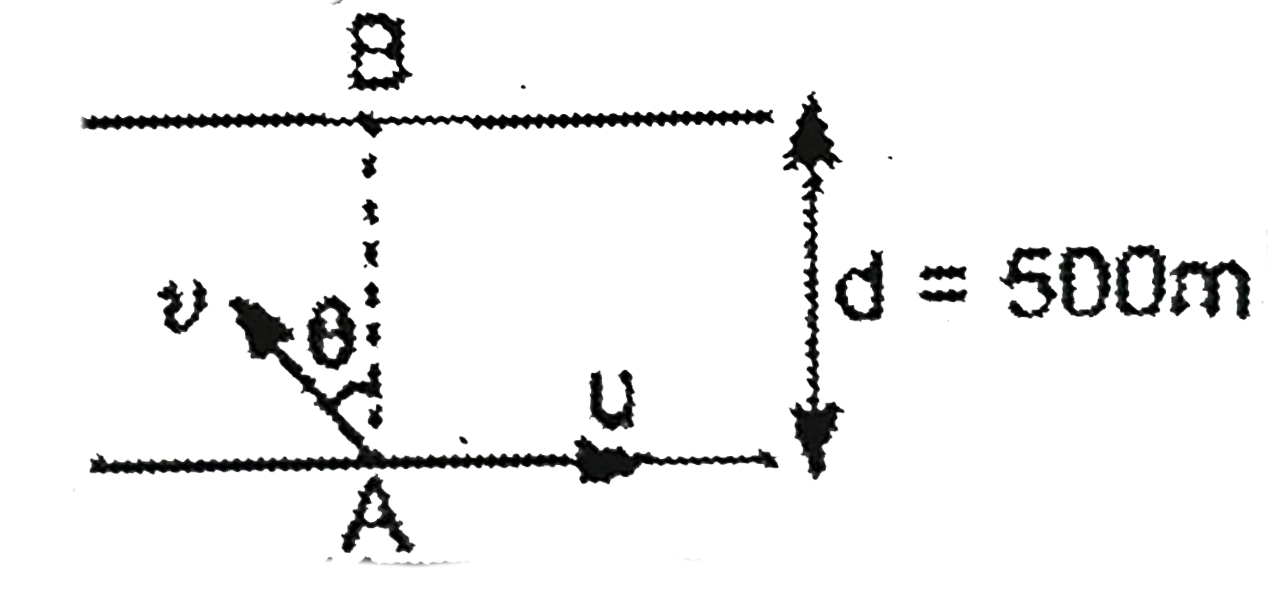
To cross the river in minimum time, the value of θ should be:
0∘
90∘
30∘
60∘
The correct Answer is:A
Step by step video, text & image solution for A swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle theta with the perpendicular as shown ip. the. figure. To cross the river in minimum time, the value of theta should be: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A swimmer wishes to cross a 500m wide river flowing at a rate 5km/hr. His speed with respect to water is 3km/hr. (a) If the heads in a direction making an angle θ with the flow, he takes to cross the river. (b) Find the shortest possible time to cross the river.
View SolutionA swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. The man has to reach the other shore at the point directly opposite to his starting point. If the reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
View Solution
Knowledge Check
A swimmer whishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle θ with the perpendicular as shown in the figure.
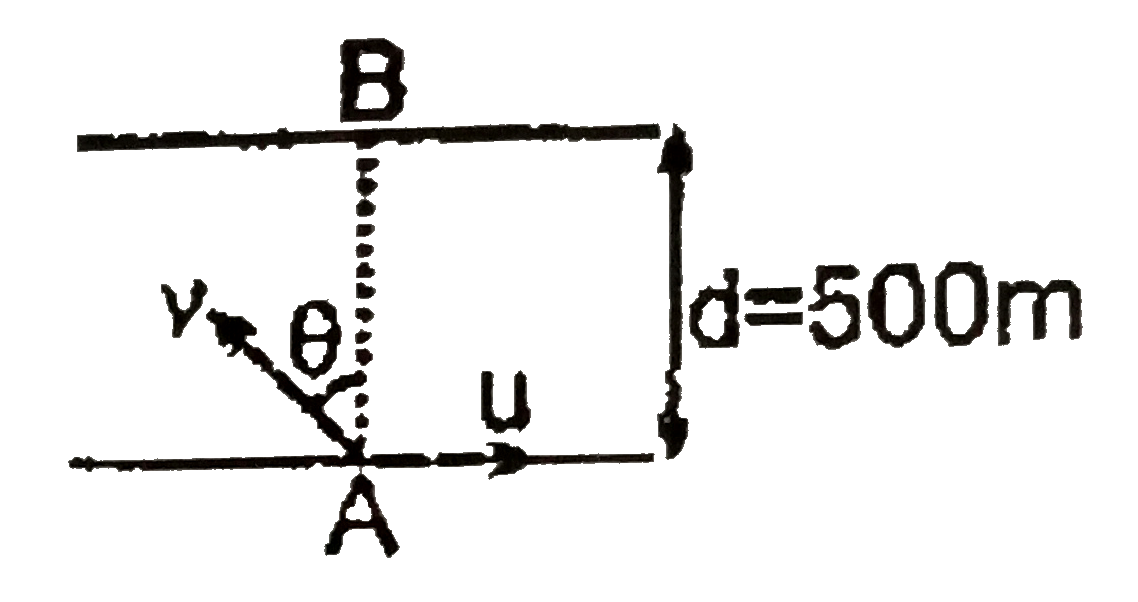
For u = 5 km/hrand v=3km//hr, the swimmer :ACan reach B in 7.5 min.BCan reach B in 6 min.CCan reach B in less than 6 minDCan never reach BA swimmer wishes to cross a river 500m width flowing at a rate u. his speed w.r.t. still water is v. for this he makes an angle θ with the vertical as shown in the given figure then:
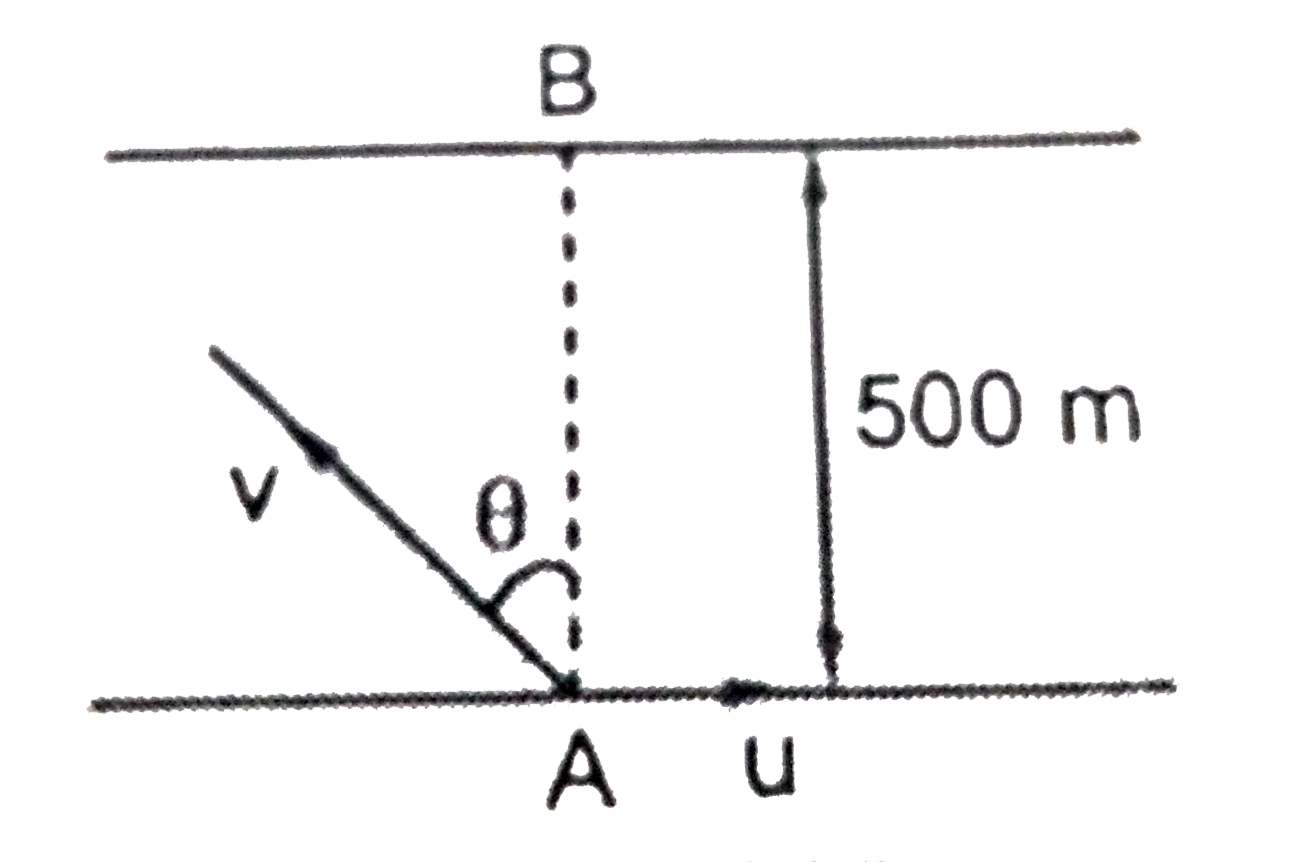 Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.A swimmer wishes to cross a 500−m river flowing at 5kmh−1. His speed with respect to water is 3kmh−1. The shortest possible time to cross the river is.
A10minB20minC6minD7.5min
A man wishes to cross a river which is flowing at a certain speed . Man uses a motor boat whose velocity with respect to water is more than speed of flow. Minimum possible time the boat takes to cross the river is t1 , but drift along the length of river is x . When boat takes shortest route to cross the river , then it takes time t2 . Find the velocity of boat with respect to water .
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
View SolutionA river 500m wide is flowing at a rate of 4m/s. A boat is sailing at a velocity of 10m/s with respect to the water, in a direction perpendicular to the river. The time taken by the boat to reach the opposite bank
View Solution

