
To find the perimeter of trapezoid ABCD above, first draw ¯¯¯¯¯¯EC parallel to ¯¯¯¯¯¯AD thereby forming rectangle ABCD, which means that EC=AD=12andEA=CD=4.
The correct Answer is:38
Step by step video, text & image solution for To find the perimeter of trapezoid ABCD above, first draw overline(EC) parallel to overline(AD) thereby forming rectangle ABCD, which means that EC=AD=12 and EA=CD=4. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:Multiple Choice
Explore 99 Videos
- ADDITIONAL TOPICS IN MATHBook:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATHExercise:Grib-In
Explore 32 Videos
- ADDITIONAL TOPICS IN MATH Book:ENGLISH SATChapter:ADDITIONAL TOPICS IN MATH Exercise:PRACTICE TEST
Explore 24 Videos
- COMPLEX NUMBERSBook:ENGLISH SATChapter:COMPLEX NUMBERSExercise:EXERCISE
Explore 6 Videos
Similar Questions
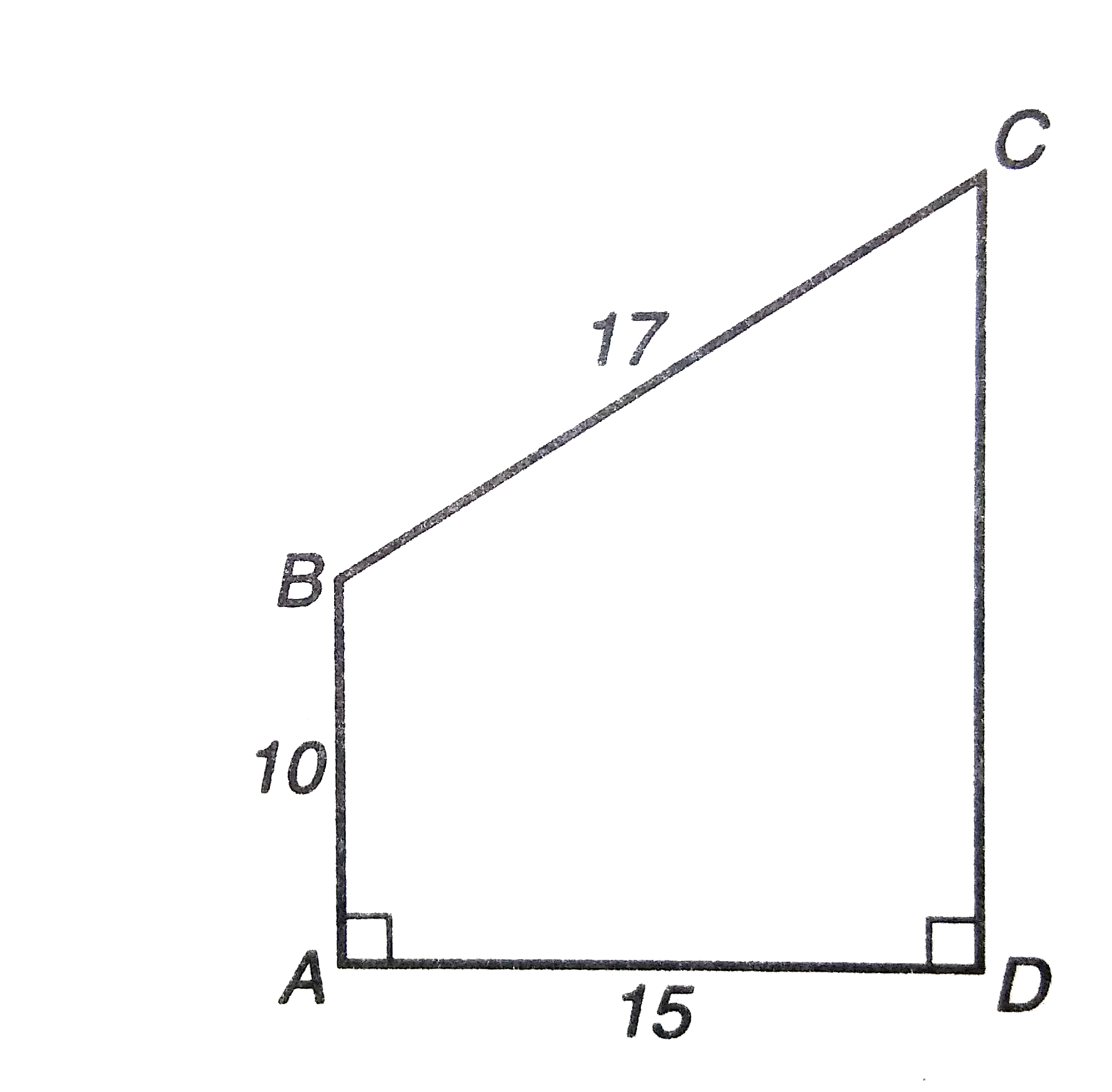
To find the area of trapezoid ABCD, first the length of base CD by drawing heigth BH to CD. Since parallel lines are everywhere equidistant, BH=AD=15. The lengths of the sides of right triangle BHC from an (8-15-17) Pythagorean triple, where CH=8. Thus, CD=CH+HD=8+10=18.
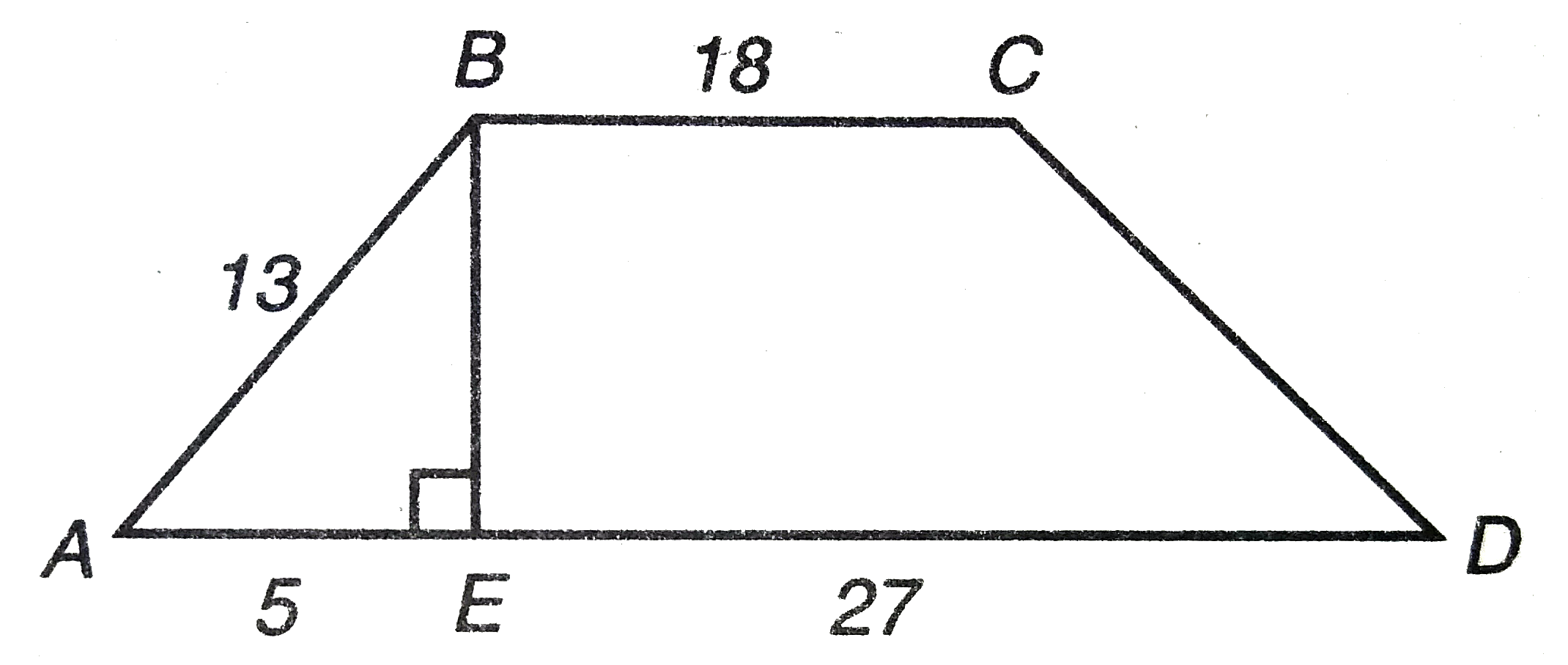
View SolutionTo find the area of trapezoid ABCD, use the fact that the lengths of the sides of right triangle AEB form a (5-12-13) Pythagorean triple, where height BE=12. The length of lower base AD=AE+ED=5+5+27=32
View Solution
Knowledge Check
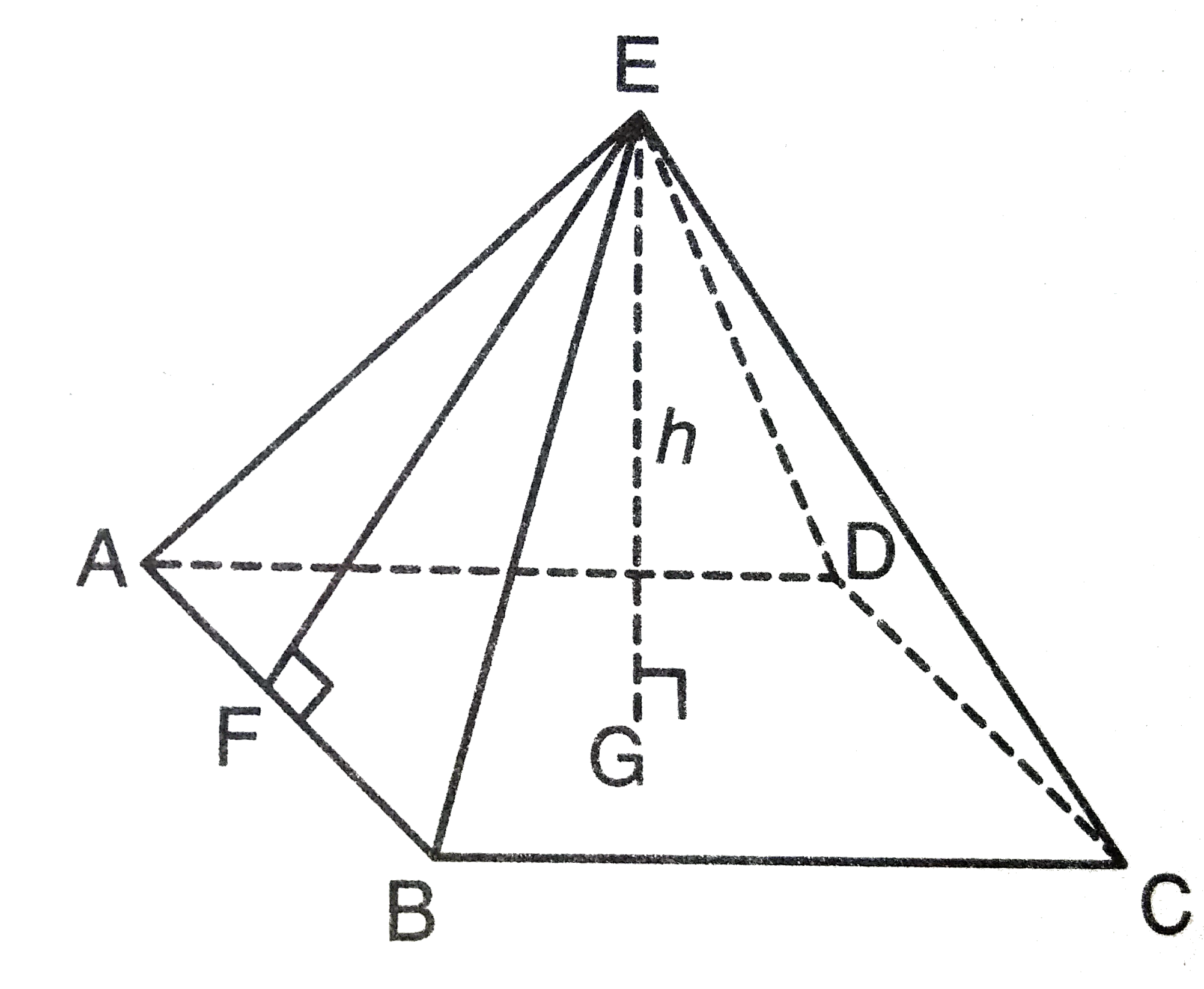
In the pyramid shown in the diagram above G is the certer of square base ABCD, ¯¯¯¯¯¯EF⊥¯¯¯¯¯¯AB and h height of the pyramid. Which statements must be true?
I. EA=EC
II. △BFC is isosceles
III. EF=EGAI and II onlyBI and III onlyCI onlyDII onlyIn the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD, AD=42, AB=12, and CD=16, what is the length of ¯¯¯¯¯¯DE?
A21B24C27D30
Calculate the area of quadrilateral ABCD In which ∠A=90∘,AB=16cm.AD=12cmandBC=CD=12.5cm
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that:
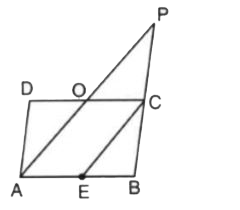
PB=2AD
View SolutionIn parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P. Prove that :
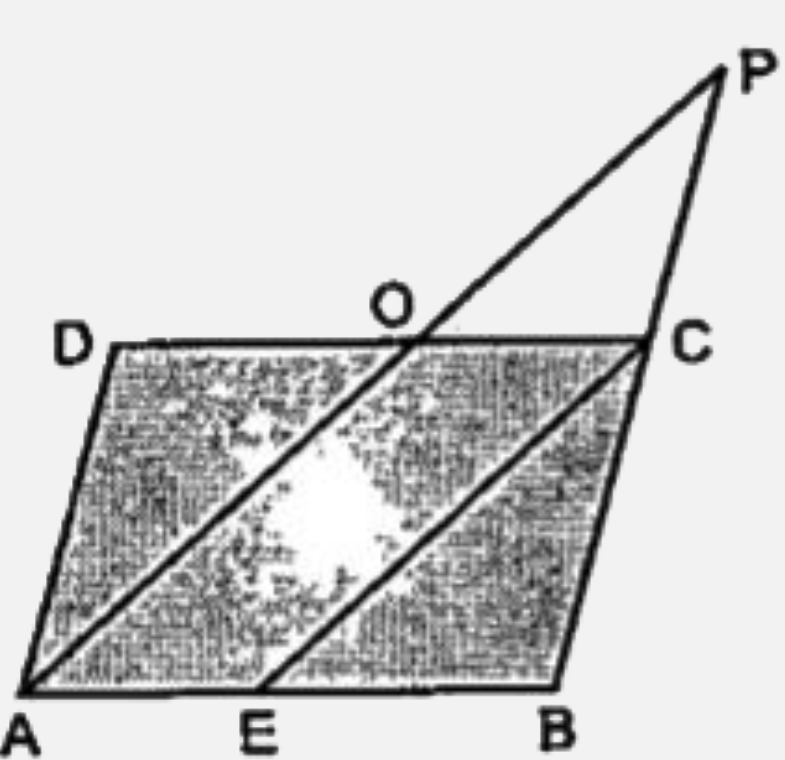
BP=2AD
View SolutionLength of the fence of a trapezium shaped field ABCD is 120m. If BC=48m,CD=17mandAD=40m, find the area of this field. Side AB is perpendicular to the parallel sides ADandBC.
View SolutionLength of the fence of a trapezium shaped field ABCD is 120m. If BC=48m,CD=17mandAD=40m, find the area of this field. Side AB is perpendicular to the parallel sides ADandBC.
View SolutionConsider a rectangle ABCD formed by the points A=(0,0), B= (6, 0), C =(6, 4) and D =(0,4), P (x, y) is a moving interior point of the rectangle, moving in such a way that d(P,AB)≤min{d(P,BC),d(P,CD)andd(P,AD)} here d (P, AB), d (P, BC), d (P, CD) and d (P, AD) represent the distance of the point P from the sides AB, BC, CD and AD respectively. Area of the region representing all possible positions of the point P is equal to (a) 8 sq. units (b) 4 sq. units (c) 12 sq. units (d) 6 sq. units
View Solution
