A vertical beam of light of cross sectional radius R2 is incident symmetrically on the curved surface of a glass hemisphere of refractive index μ=32. Radius of the hemisphere is R and its base is on a horizontal table. Find the radius of luminous spot formed on the table. sin20∘=13 and sin80∘=0.98
Step by step video & image solution for A vertical beam of light of cross sectional radius (R)/(2) is incident symmetrically on the curved surface of a glass hemisphere of refractive index mu = (3)/(2). Radius of the hemisphere is R and its base is on a horizontal table. Find the radius of luminous spot formed on the table. sin 20^(@) = (1)/(3) and sin 80^(@) = 0.98 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Practive Exercise 5.5
Explore 12 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Practive Exercise 5.6
Explore 16 Videos
- GEOMETRICAL OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:GEOMETRICAL OPTICSExercise:Practive Exercise 5.3
Explore 12 Videos
- ELECTROSTATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:ELECTROSTATICSExercise:Unsolved Numberical Problems
Explore 73 Videos
- HEAT AND THERMAL EXPANSIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT AND THERMAL EXPANSIONExercise:UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
Explore 82 Videos
Similar Questions
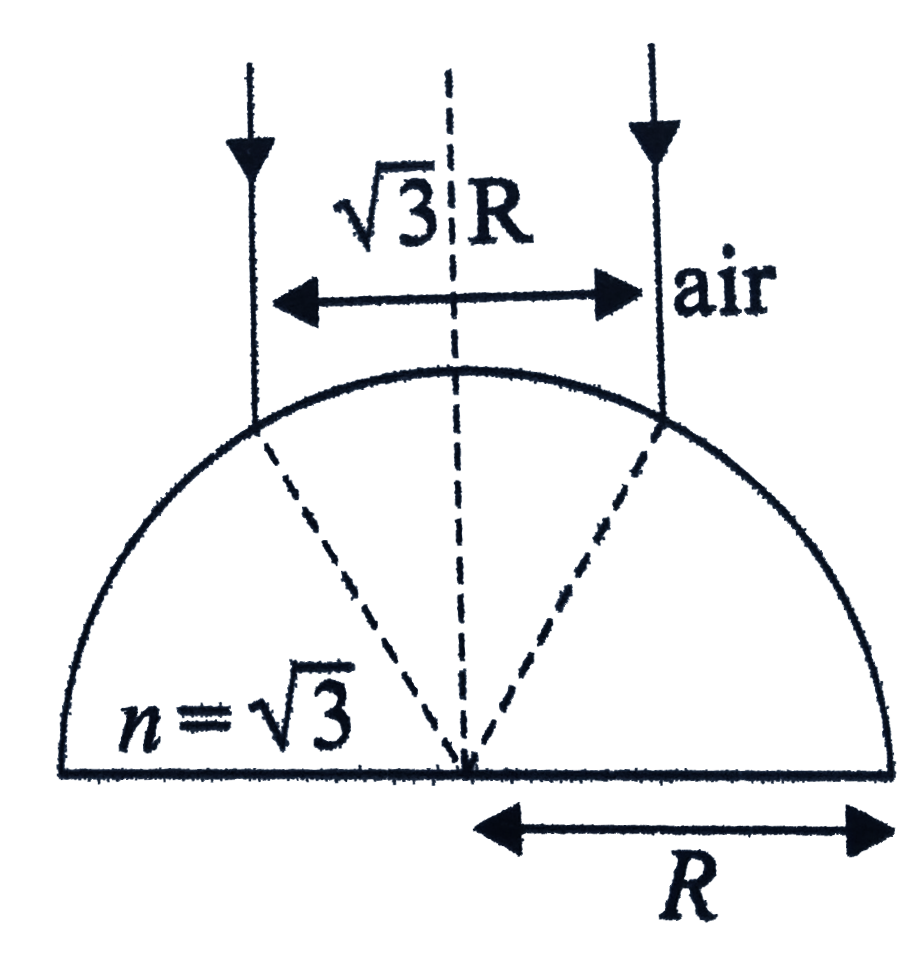
A light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :

View Solution
Knowledge Check
A parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6cm and refractive index 1.5, placed in air as shown in figure (i). Assume paraxial ray approxiamtion.
 .AThe rays are focused at 12cm from the point P to the right, in the solutation as shown in figure (i)BThe rays are focused at 16cm from the point P to the right, in the situation as shown in figure (i).CIf the rays are incident at the curved surface (figure (ii)) then these are focused at distance 18cm from point P to the rightDIf the ray are incident at the curved surface (figure(ii)) then these are focused at distance 14cm from point P to the right.
.AThe rays are focused at 12cm from the point P to the right, in the solutation as shown in figure (i)BThe rays are focused at 16cm from the point P to the right, in the situation as shown in figure (i).CIf the rays are incident at the curved surface (figure (ii)) then these are focused at distance 18cm from point P to the rightDIf the ray are incident at the curved surface (figure(ii)) then these are focused at distance 14cm from point P to the right.Find the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:
 A(μ−1)RμBμR(μ−1)CR(μ−1)D(μ−1)R2μ
A(μ−1)RμBμR(μ−1)CR(μ−1)D(μ−1)R2μA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
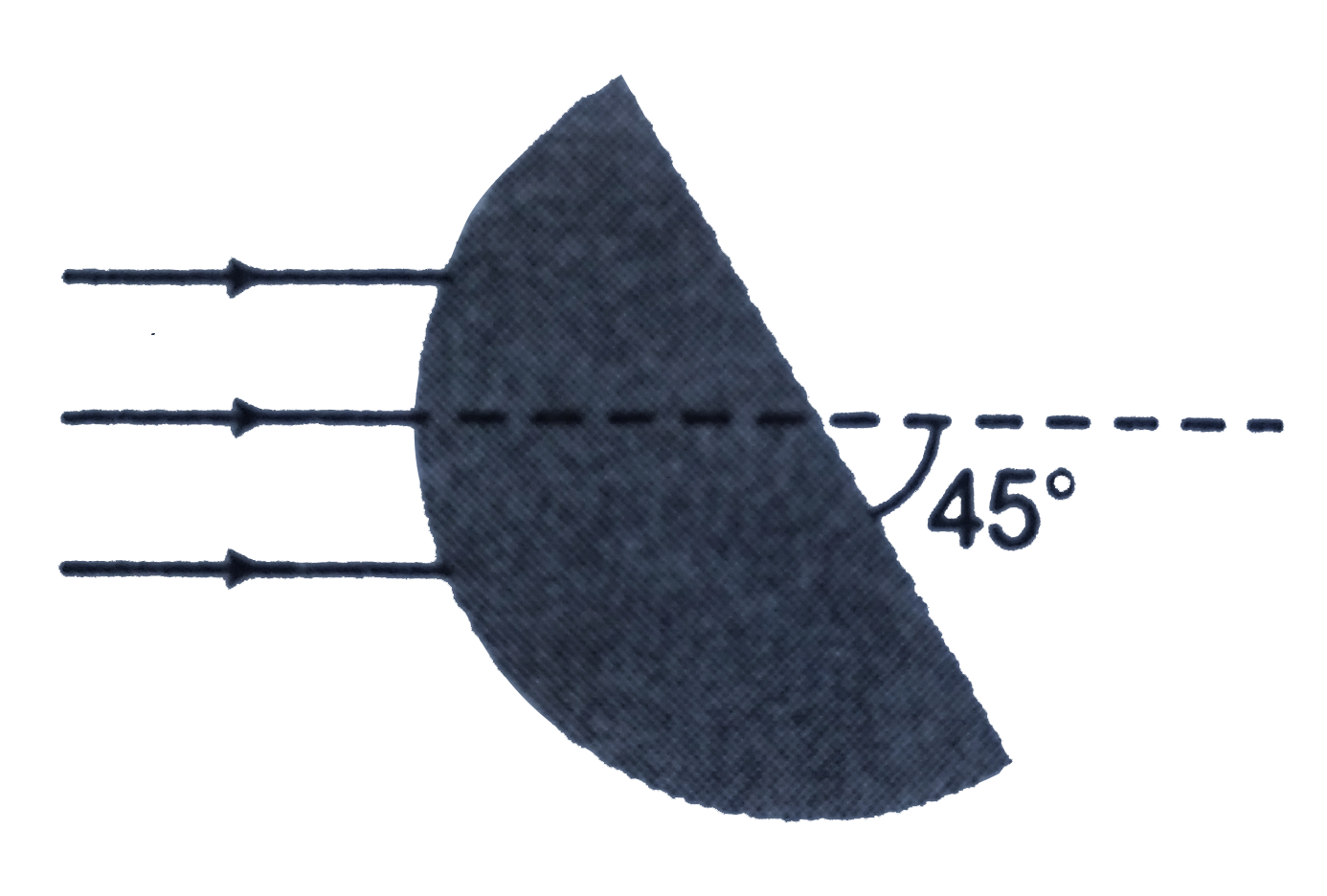 AR2B3RCR3D2R
AR2B3RCR3D2R
Radius of curvature of two surfaces of a glass convex lens is 20cm each. If refractive index of glass is 3/2, what is the power of lens in D ?
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionThe plane surface of a plano-convex lens of refracting index 1.5, is silvered. The radius of curvature of curved surface is R. Find the focal length of the mirror thus formed.
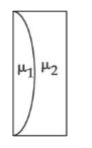
View SolutionCurved surfaces of a plano-convex lens of refractive index μ1 and a plano-concave lens of refractive index μ2 have equal radius of curvature as shown in figure. Find the ratio of radius of curvature to the focal length of the combined lenses.
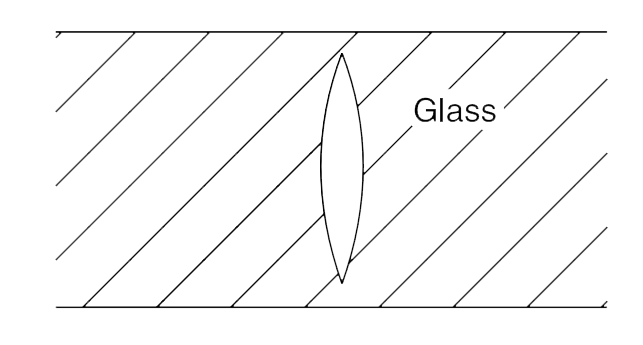
View SolutionThere is an air lens in an extended glass medium. The radius of curvature of both the curved surfaces is R, and refractive index of the glass is 32 . Power of this air lens is P. Find the refractive index of the material to be filled inside the lens so that its power becomes – P.
View Solution

