A particle is resting on an inverted cone as shown. It is attached to cone by a thread of length 20 cm. String remains parallel to slope of cone. The cone is givenangular acceleration of 0.5rad/sec2 then at what time does mass leave contact with surface (assuming sufficient friction) :
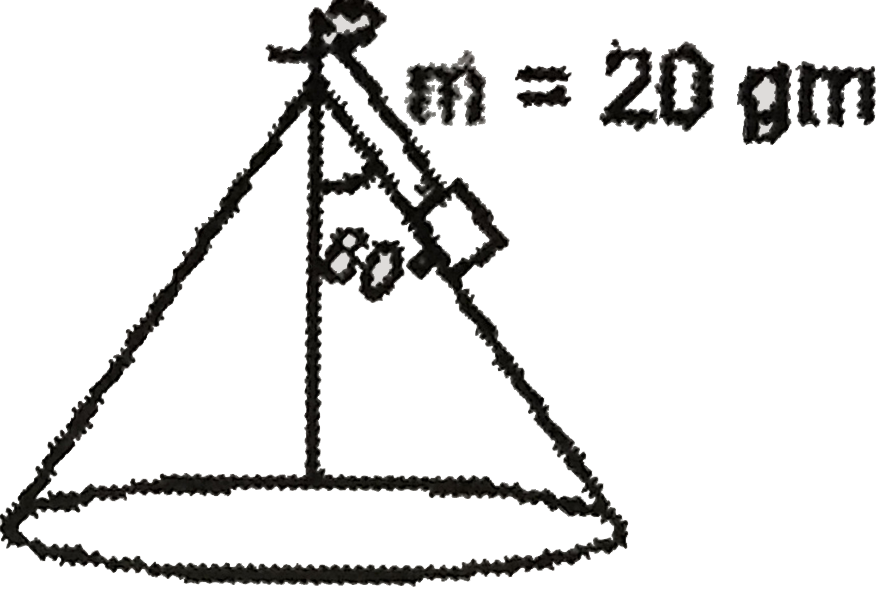
20sec
10sec
40sec
5sec
The correct Answer is:a
Step by step video, text & image solution for A particle is resting on an inverted cone as shown. It is attached to cone by a thread of length 20 cm. String remains parallel to slope of cone. The cone is givenangular acceleration of 0.5 rad//sec^(2) then at what time does mass leave contact with surface (assuming sufficient friction) : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-2
73 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-3
49 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Example
95 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
Similar Questions
A block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9μ=0.5 and g=10ms−2
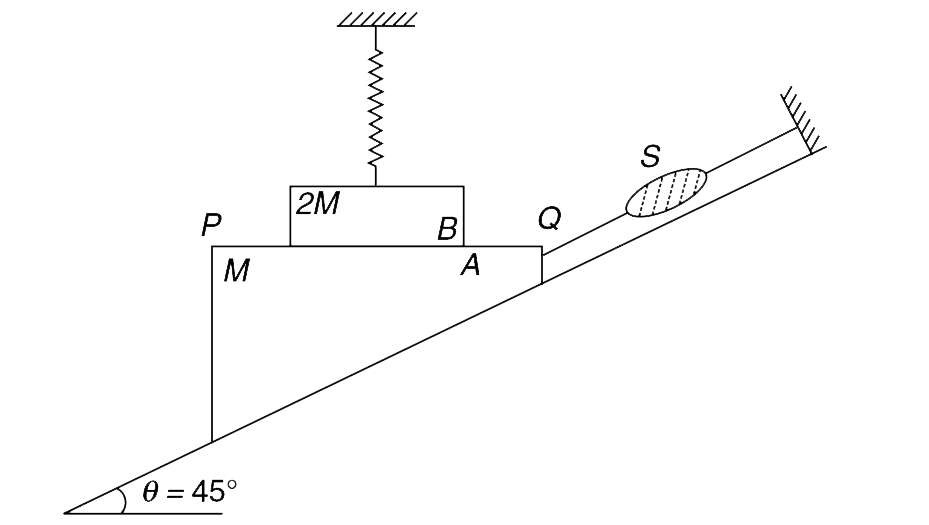
View SolutionThe system shown in figure is in equilibrium. Surface PQ of wedge A, having mass M, is horizontal. Block B, having mass 2M, rests on wedge A and is supported by a vertical spring. The spring balance S is showing a reading of √2 Mg. There is no friction anywhere and the thread QS is parallel to the incline surface. The thread QS is cut. Find the acceleration of A and the normal contact force between A and B immediately after the thread is cut.
View Solution
Knowledge Check
A samll object of mass 10.0 g is at rest 30.0 cm from a horizontal disk's centre. The disk starts to rotate from rest about its centre with a constant angular acceleration of 4.50 rad/s2. What is the magnitude of the net force acting on the object after a time of t=13 s if the object remains at rest with respect to the disk ?
A0NB1.5×10−2NC7.4×10−3ND1.8×10−2N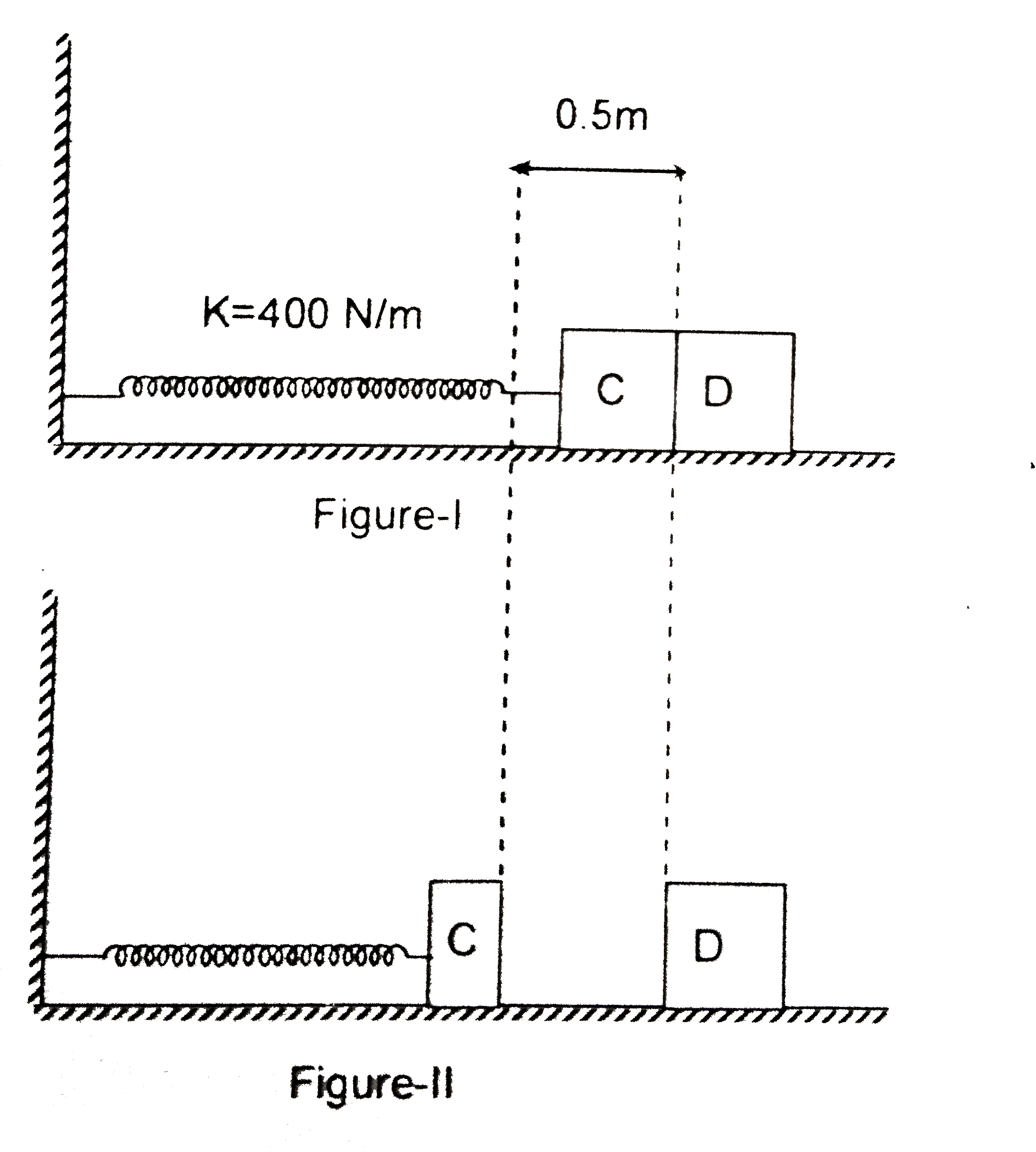
A massless spring of stiffness 400 N/m is fastened at left end to a vertical wall as shown in the figure I. initially block C of mass 2 kg and block D of mass 5 kg rest on horizontal surface with block C in contact with spring (But not compressiong it.) and the block D in contact with block C block C is moved leftward compressing spring by a distance of 0.5 m and held in place while block D remains at rest as shown in the figure. Now block C is released and it accelerates to the right towards block D the surface is rough and the coefficient of friction between each block and surface is 0.1 The block collide Instantaneously stick together and move right find the velocity of combined system just after collision.A2 m/sB3 m/sC4 m/sD6 m/sA block of mass m is kept on a smooth surface. It is also in contact with a thin plank of mass M=2m, one end of which is clamped to a wall as shown in the figure. The length of the plank is L. The block is given an initial velocity v0, towards right and initially the block is at a distance x0 from hinge. Coefficient of friction between the plank and block is μ.
Assume that througout the motion block remains, below the rod, then at what position from the fixed point it will stop?
(GIven β=v202μgL)
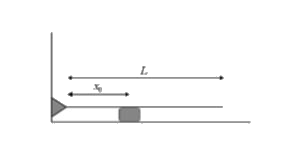 Ax0e2βBx0eβCx0e−2βDx0e−β
Ax0e2βBx0eβCx0e−2βDx0e−β
One twirls a circular ring (of mass and radius ) near the tip of one’s finger as shown in Figure 1. In the process the finger never loses contact with the inner rim of the ring. The finger traces out the surface of a cone, shown by the dotted line. The radius of the path traced out by the point where the ring and the finger is in contact is ?. The finger rotates with an angular velocity 20. The rotating ring rolls without slipping on the outside of a smaller circle described by the point where the ring and the finger is in contact (Figure 2). The coefficient of friction between the ring and the finger is μ and the acceleration due to gravity is g.

The minimum vlaue of ω0 below which the ring will drop down is
View SolutionA particle B of mass 5 kg is attached to a frictionless pivot A by a thread of length d = 0.2 m so that B hangs freely. At some instant of time a strong wind begins to apply a constant horizontal force F = 100 N to B, as a result it rotates about A in a vertical plane. Find the speed (in m/s) of B at the instant when the string is horizontal (g=10ms2)
View SolutionA small cubical block of mass 1kg is placed inside a rough rectangular groove made in a circular rough table as shown in the figure. The coefficient of friction for afl the rough surfaces is μ=0.5. The table starts rotating clockwise with angular acceleration 1rads2 in ahorizontal plane about its axis. Find the time (in's) after which the block will start moving with respect to the table. Assume the size of block slightly smaller then the width of groove.
'(##CEN_KSR_PHY_JEE_C07_040_Q25##)'
View SolutionA round cone A of mass m=3.2kg and half-angle α=10∘ rolls uniformly and without slipping along a round conical surface B so that its apex O remains stationary (figure). The centre of gravity of the cone A is at the same level as the point O and at a distance l=17cm from it. The cone's axis moves with angular velocity ω. Find:
(a) the static friction force acting on the cone A, if ω=1.0rad/s,
(b) at what values of ω the cone A will roll without sliding, if the coefficient of friction between the surfaces is equal to k=0.25.
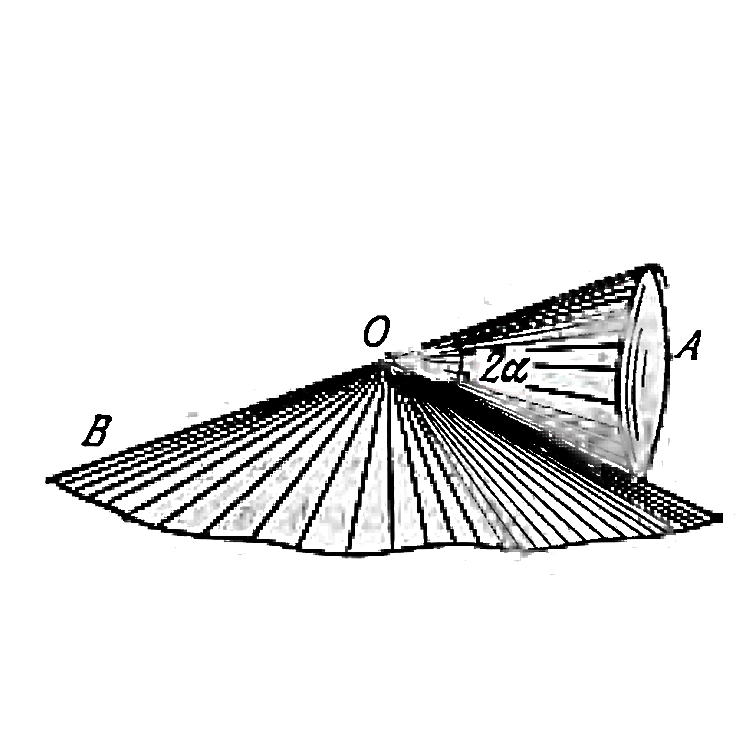
View SolutionA small sized mass m is attached by a massless string (of length L) to the top of a fixed frictionless solid cone whose axis is vertical. The half angle at the vertex of cone is theta. If the mass m moves around in a horizontal circle at speed v , what is the maximum value of v for which mass stay in contact with the comes? (g is acceleration due to gravity.)
View Solution
