The mass in the fig. can slide on a frictionless surface. The mass is pulled out by a distance x. The spring constants are k1 and k2 respectively. Find the force pulling back on the mass and orce on the wall.

Step by step video & image solution for The mass in the fig. can slide on a frictionless surface. The mass is pulled out by a distance x. The spring constants are k_(1) and k_(2) respectively. Find the force pulling back on the mass and orce on the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - level 1
103 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Level-2
73 Videos
- FORCE ANALYSISBOOK - ANURAG MISHRACHAPTER - FORCE ANALYSISEXERCISE - Matching type
13 Videos
- DESCRIPTION OF MOTIONBOOK - ANURAG MISHRACHAPTER - DESCRIPTION OF MOTIONEXERCISE - Level-3
34 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
Similar Questions
Two masses m1andm2 re connected by a spring of spring constnt k and are placed on as frictionless horizontal surface. Initially the spring is tretched through a distance x0 when the system is released from rest. Find the distance moved by the tow masses before they again come to rest.
View SolutionIn Fig. three identical massless springs are kept horizontal. The left end of the first is tied to a wall. The left end of the second spring is tied to a block of mass m placed on rough ground and the ,eft end of the third spring is tied to a block of mass m placed frictionless ground. The right end of each spring is pulled by a force that is increased gradually from zero to F. Extensions in these springs are x1, x2 and x3, respectively. Find the relationship between x1, x2, and x3

View Solution
Knowledge Check
The mass in the figure can slide on a frictionless surface. When the mass is pulled out, spring 1 is stretched a distance x1and spring 2 is stretched a distance x2. The spring constants are k1andk2 respectively. Magnitude of spring force pulling back on the mass is
 Ak1x1Bk2x2C(k1x1+k2x2)D0.5(k1+k2)(x1+x2)
Ak1x1Bk2x2C(k1x1+k2x2)D0.5(k1+k2)(x1+x2)A mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is
 AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mg
AmgK1+K2Bmg(K1+K2)K1K2CmgK1K2K1+K2DK1+K2K1K2mgThree masses are connected as shown in figure on a horizontal frictionless surface and pulled by a force of 60 N. The tensions T1andT2 are in the ratio
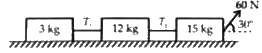 A1:1B1:5C1:4D4:5
A1:1B1:5C1:4D4:5
Three masses are connected as shown in figure on a horizontal frictionless surface and pulled by a force of 60 N. The tensions T1andT2 are in the ratio
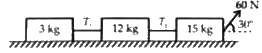
View SolutionTwo blocks (1 and 2) of equal mass m are connected by an ideal string (see figure shown) over a frictionless pulley. The blocks are attached to the ground by springs having spring constants k1 and k2 such that k1>k2
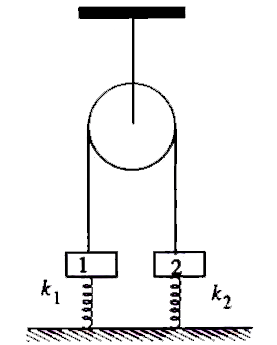
Initially, both springs are unstretched. The block 1 is slowly pulled down a distance x and released. Just after the release the possible values of the magnitude of the acceleration of the blocks a1 and a2 can be–
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View SolutionA block is placed on a frictionless horizontal table. The mass of the block is m and springs are attached on either side with force constants K1andK2 . If the block is displaced a little and left to oscillate, then the angular frequency of oscillation will be
View Solution
