A sphere is projected npon a rough inclined plane. The friction coefficient between the solid sphere and the incline isμ. The centre of the sphere is given an initial upward' velocity at t=0 without imparting any initial angular velocity. Then, which of the following statement (s) is/are true?
Pure rolling will defin!tely begin before the sphere reaches the highest point and the sphere will continue to roll purely after that, even while coming down.
Pure rolling will definitely begin before the sphere reaches the highest point but the sphere will continue to roll purely after that (even while coming down) only· if μ is greater- than a certain value.
The sphere will be rolling purely while coming down if μ>(2tanα)7
The sphere cannot roll purely while moving up the incline
The correct Answer is:B, C
Step by step video, text & image solution for A sphere is projected npon a rough inclined plane. The friction coefficient between the solid sphere and the incline ismu. The centre of the sphere is given an initial upward' velocity at t=0 without imparting any initial angular velocity. Then, which of the following statement (s) is/are true? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - COMPREHENSION_TYPE
29 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - MATCH THE COLUMN
12 Videos
- RIGID BODY MOTIONBOOK - ANURAG MISHRACHAPTER - RIGID BODY MOTIONEXERCISE - SCQ_TYPE
83 Videos
- IMPULSE AND MOMENTUMBOOK - ANURAG MISHRACHAPTER - IMPULSE AND MOMENTUMEXERCISE - matching
3 Videos
- UNIT AND DIMENSIONSBOOK - ANURAG MISHRACHAPTER - UNIT AND DIMENSIONSEXERCISE - Matching Type Problem
4 Videos
Similar Questions
A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is μ=0.5 and radius R, then find
(a) Time when linear velocity becomes zero
(b) Angular velocity at that instant

View SolutionA solid cylinder of mass m is resting on fixed rough inclined plane with help of a thread. Find friction force between cylinder and inclined plane. (given μ=0.4)

View Solution
Knowledge Check
A Sphere pure rolls on a rough inclined plane with initial velocity 2.8 m/s. Find the maximum distance on the inclined plane
 A2.74 mB5.48 mC1.38 mD3.2 m
A2.74 mB5.48 mC1.38 mD3.2 mA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.
A sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
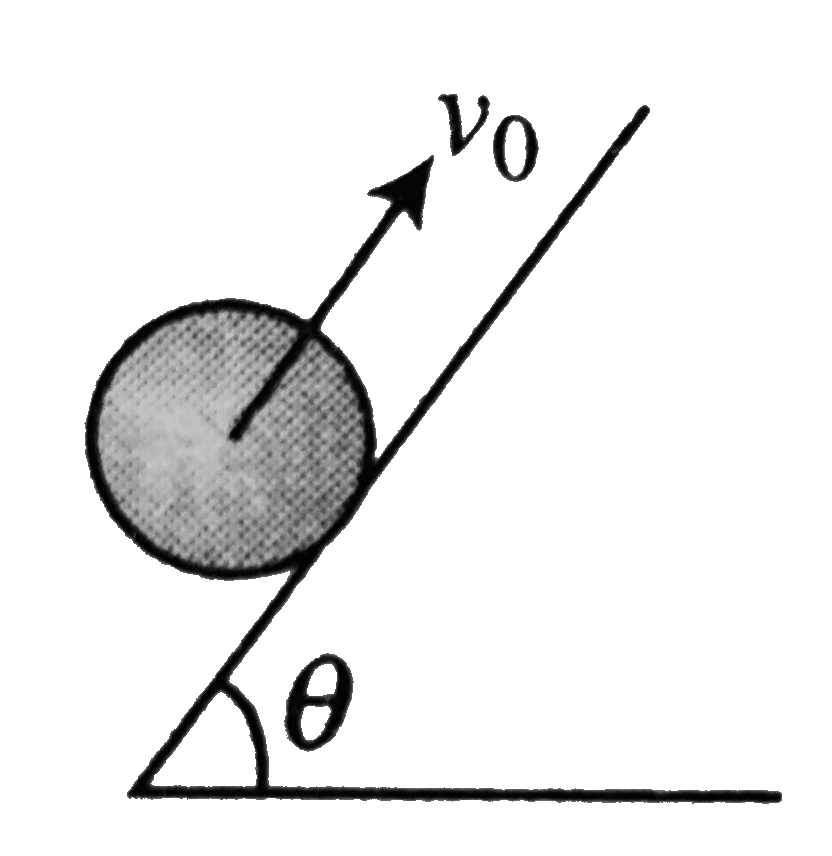
View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA solid sphere of mass m is lying at rest on a rough horizontal surface. The coefficient of friction between the ground and sphere is μ. The maximum value of F, so that the sphere will not slip, is equal to

View SolutionA solid sphere is given an angular velocity ζ and kept on a rough fixed incline plane. The choose the correct statement.

View Solution
