A sample of an ideal gas is expanded to in a reversible process for which , with What is work done by the gas (in kJ) ?
The correct Answer is:5200
To find the work done by the gas during its expansion from 1m3 to 3m3 under the given conditions, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by the gas during an expansion is given by the integral:
W=∫V2V1PdV
where V1 and V2 are the initial and final volumes, respectively.
Step 2: Substitute the Pressure Equation
We are given that the pressure P is related to the volume V by the equation:
P=KV2
where K=6bar/m6. Substituting this into the work done formula gives:
W=∫31KV2dV
Step 3: Factor Out the Constant
Since K is a constant, we can factor it out of the integral:
W=K∫31V2dV
Step 4: Evaluate the Integral
Now we need to evaluate the integral ∫V2dV:
∫V2dV=V33
Now we can apply the limits from 1 to 3:
W=K(V33)31=K(333−133)
Calculating this gives:
W=K(273−13)=K(9−13)=K(27−13)=K(263)
Step 5: Substitute the Value of K
Now substituting K=6bar/m6:
W=6(263)=1563=52bar⋅m3
Step 6: Convert Units
Since 1bar⋅m3=100kJ, we convert the work done:
W=52bar⋅m3×100kJ/bar=5200kJ
Final Answer
Thus, the work done by the gas is:
5200kJ
The work done W by the gas during an expansion is given by the integral:
W=∫V2V1PdV
where V1 and V2 are the initial and final volumes, respectively.
We are given that the pressure P is related to the volume V by the equation:
P=KV2
where K=6bar/m6. Substituting this into the work done formula gives:
W=∫31KV2dV
Since K is a constant, we can factor it out of the integral:
W=K∫31V2dV
Now we need to evaluate the integral ∫V2dV:
∫V2dV=V33
Now we can apply the limits from 1 to 3:
W=K(V33)31=K(333−133)
Calculating this gives:
W=K(273−13)=K(9−13)=K(27−13)=K(263)
Now substituting K=6bar/m6:
W=6(263)=1563=52bar⋅m3
Since 1bar⋅m3=100kJ, we convert the work done:
W=52bar⋅m3×100kJ/bar=5200kJ
Thus, the work done by the gas is:
5200kJ
Topper's Solved these Questions
Similar Questions
A sample of an ideal gas is expanded from 1dm3 to 3 in a reversible process for which P=KV3, with K=1/5(atm/dm3), what is work done by gas (Latm)
View SolutionA sample of an ideal gas is expanded to twice its original volume of 1m3 in a reversible process for which P=αV2, where α=5atmm−6. If CV,m=20Jmol−1K−1, determine moalr change in entropy (ΔSm) for the process.
View Solution
Knowledge Check
A gas expands from a volume of 1m3 to a volume of 2m3 against an external pressure of 105Nm−2. The work done of the gas will be
A105kJB102kJC102JD103JA gas expands from a volume of 1m3 to a volume of 2m3 against an external pressure of 105Nm−2. The work done of the gas will be
A105kJB102kJC102JD103J2 moles of an ideal gas is expanded isothermally from 2.5×10−3m3 to 8×10−3m3 against a constant external pressure of 5×105Nm−2. The work done in the process is ________ .
A−2.525kJB−2.750kJC−0.2525JD−2.525J
A sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?
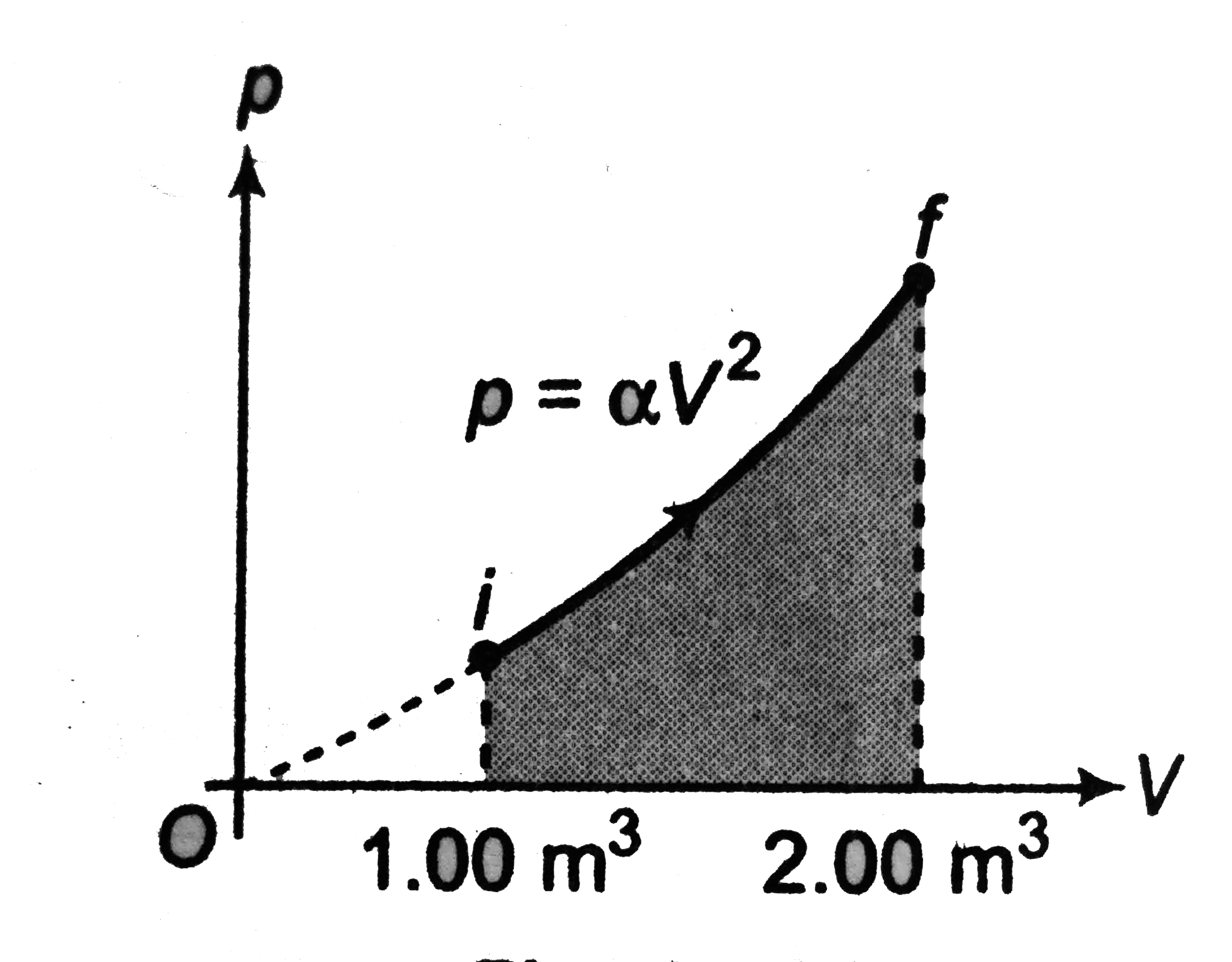
View SolutionA sample of ideal gas is expanded to twice of its original volume of 1m^(3) in a quasi-static process for which P=alpha v^(2),alpha=3*10^(5)Pa/m^(6)as shown in fig. Work done by expanding gas is
View Solution1 moles of an ideal gas expanded spontaneously into vaccum. The work done will be
View Solution1 mole of an ideal gas expands from 5dm3 to25dm3 isothermally and irreversibly at 27∘ C. Find work done in the process [R=8.3 J/mol/K]
View Solution6 moles of an ideal gas expand isothermally and reversibly from a volume of 1 litre to a volume of 10 litres at 27∘C. What is the maximum work done.
View Solution

