Value of the acceleration A of a particle moving in sample harmonic motion as a function of its displacement x are given in the table below .
A(mm s−2) 16 8 0 −8 −16
x(mm) −4 −2 0 2 4
The period of the motion is
1πs
2πs
π2s
πs
The correct Answer is:D
Step by step video, text & image solution for Value of the acceleration A of a particle moving in sample harmonic motion as a function of its displacement x are given in the table below . A("mm s" ^(-2))" "16" "8" "0" "-8" "-16 x(mm )" "-4" "-2" "0" "2" "4 The period of the motion is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given in the table below.
∣∣∣A(mms−2)1680−8−16x(mm)−4−2024∣∣∣
The pariod of the motion isA1πsB2πsCπ2sDπs - Question 2 - Select One
If a particle is executing simple harmonic motion, then acceleration of particle
Ais uniformBvaries linearly with timeCis non uniformDBoth (2) & (3) - Question 3 - Select One
A particle executes simple harmonic motion. Then the graph of veloctiy as a function of its displacement is
Aa straight lineBa circleCan ellipseDa hyperbola
The phase difference between displacement and acceleration of particle in a simple harmonic motion is
View SolutionIn simple harmonic motion, acceleration of the particle is zero, when its
View SolutionThe phase difference between displacement and acceleration of a particle in a simple harmonic motion is:
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
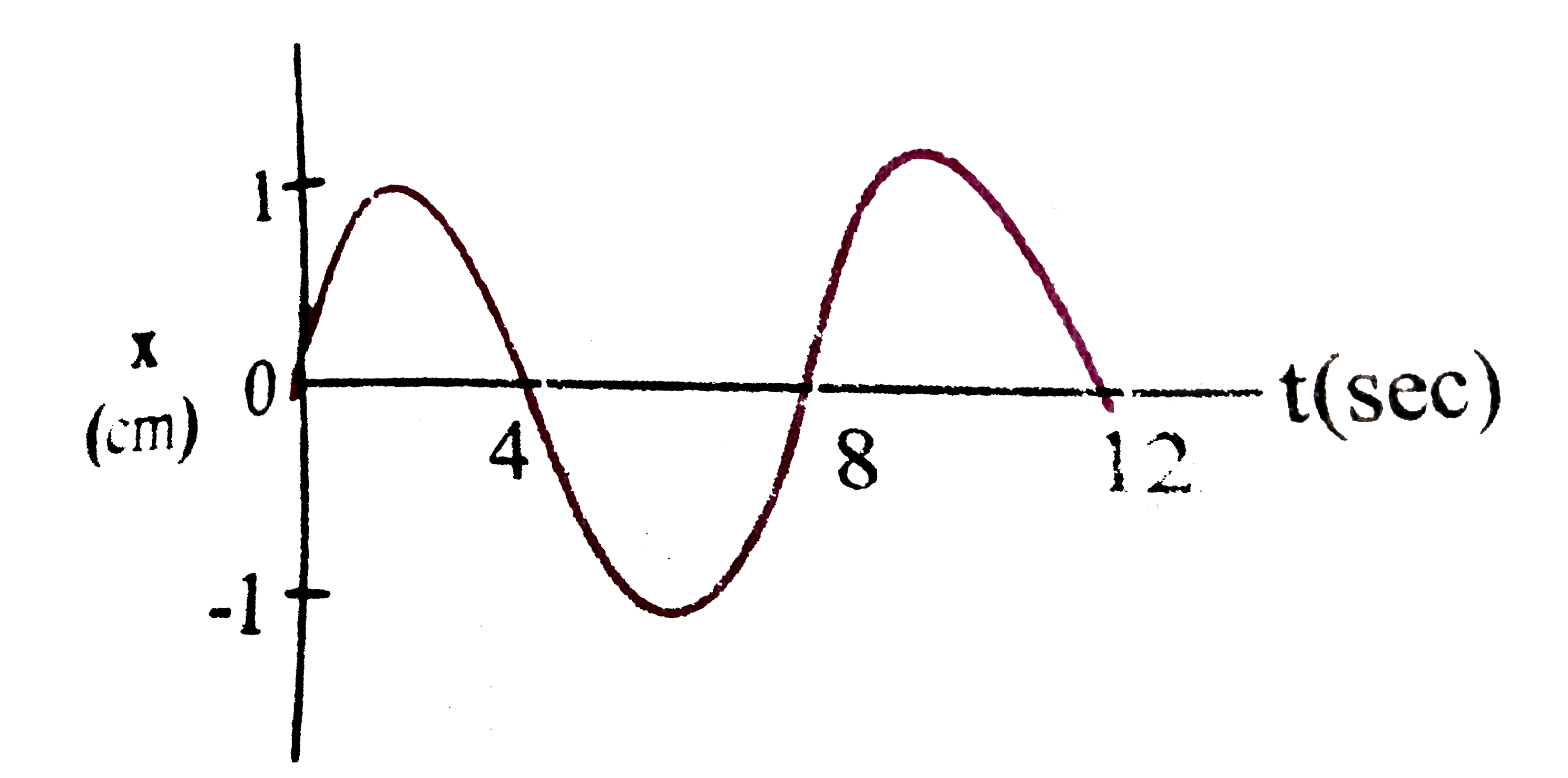
View SolutionIf the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
View Solution