Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given in the table below.
∣∣∣A(mms−2)1680−8−16x(mm)−4−2024∣∣∣
The pariod of the motion is
A
1πs
B
2πs
C
π2s
D
πs
Video Solution
Text Solution
The correct Answer is:D
[A]=ω2x⇒[A]x=ω2
From the given value [A]x=ω2=4⇒ω=2.
Also ω2=2πT⇒2=2πT⇒T=πsec
|
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Velocity , Acceleration And Energy Of Simple Harmonic Motion
40 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System
24 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
Value of the acceleration A of a particle moving in sample harmonic motion as a function of its displacement x are given in the table below .
A(mm s−2) 16 8 0 −8 −16
x(mm) −4 −2 0 2 4
The period of the motion isA1πsB2πsCπ2sDπsIf the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
A0.5s−1B0.25s−1C1s−1D2s−1The x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
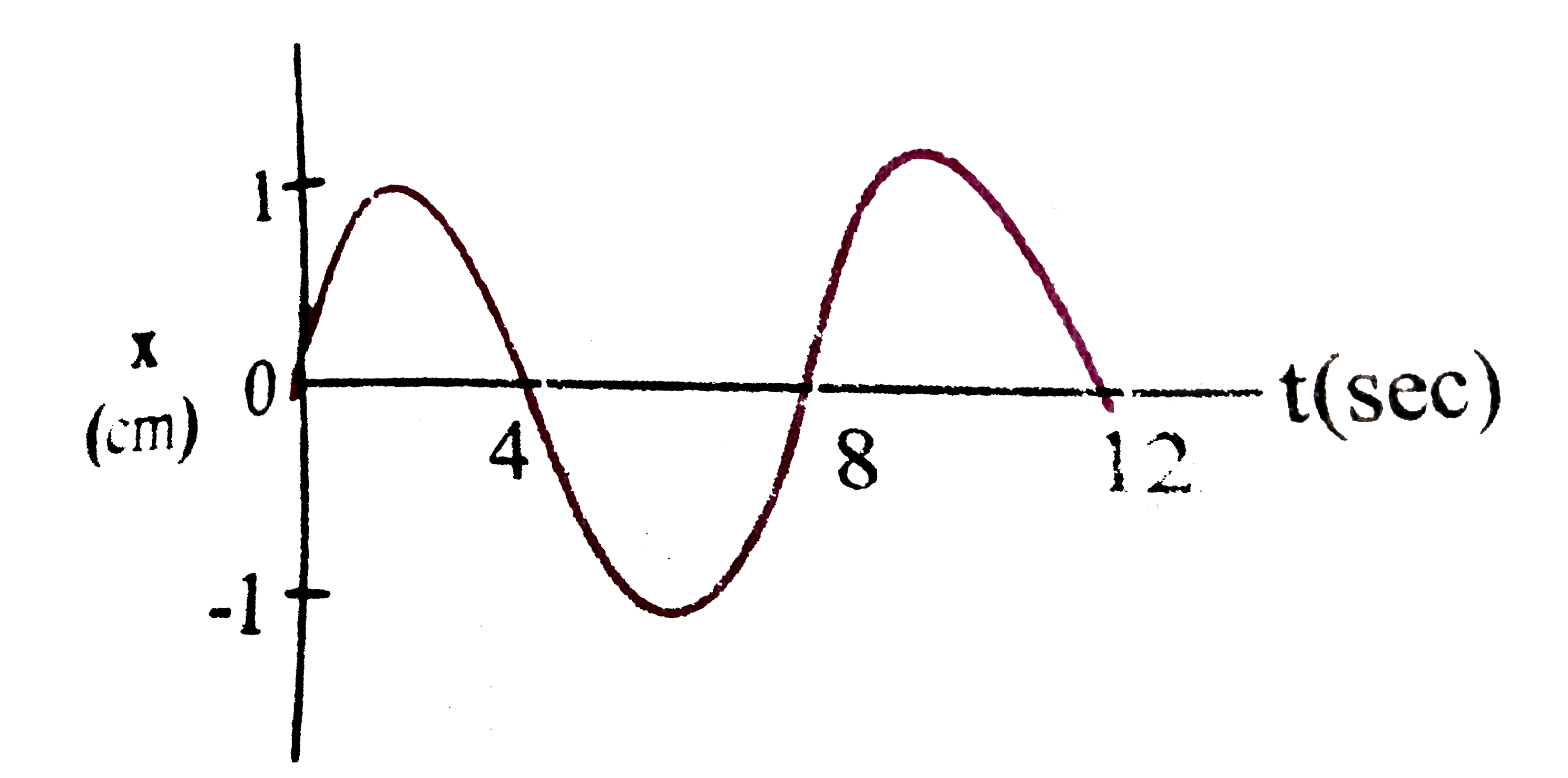 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionMaximum acceleration of an object in simple harmonic motion is 24m/s^(2) and maximum velocity is 16m/ sec. The amplitude of object is
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
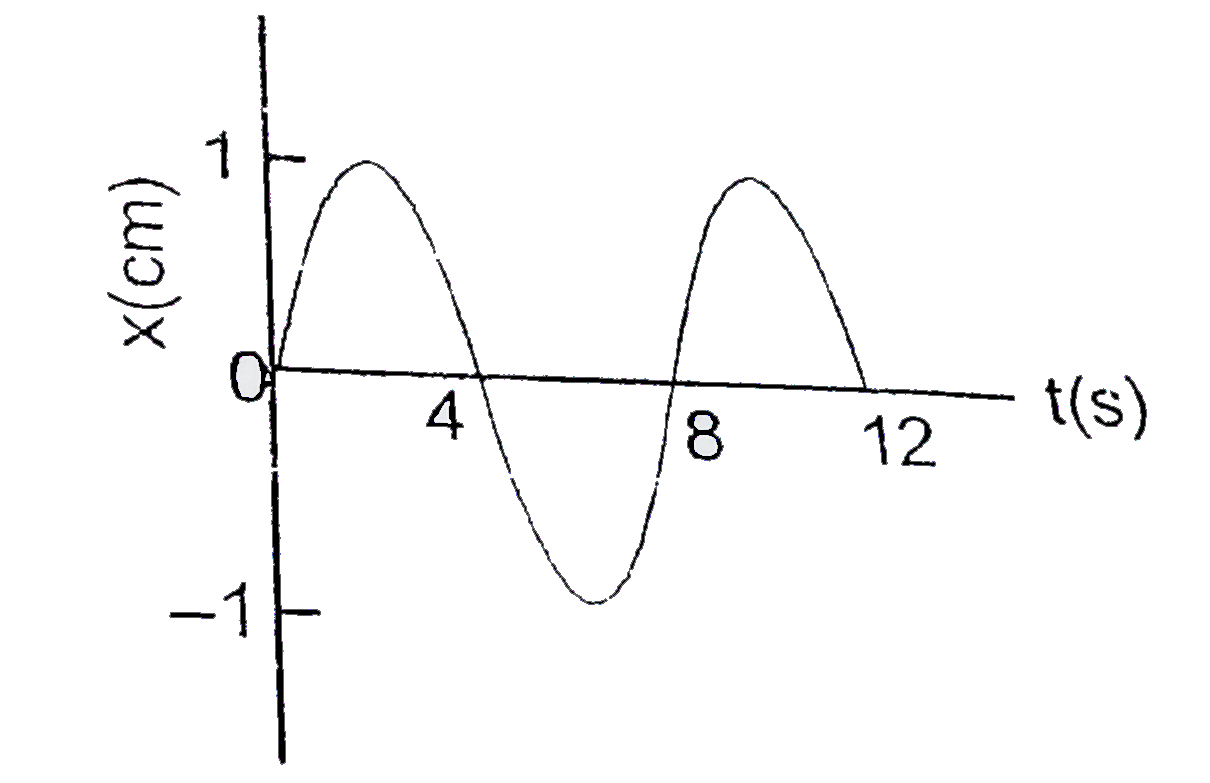
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is

View SolutionA particle executes simple harmonic motion. The amplitude of vibration of particle is 2 cm. The displacement of particle in one time period is
View Solution

