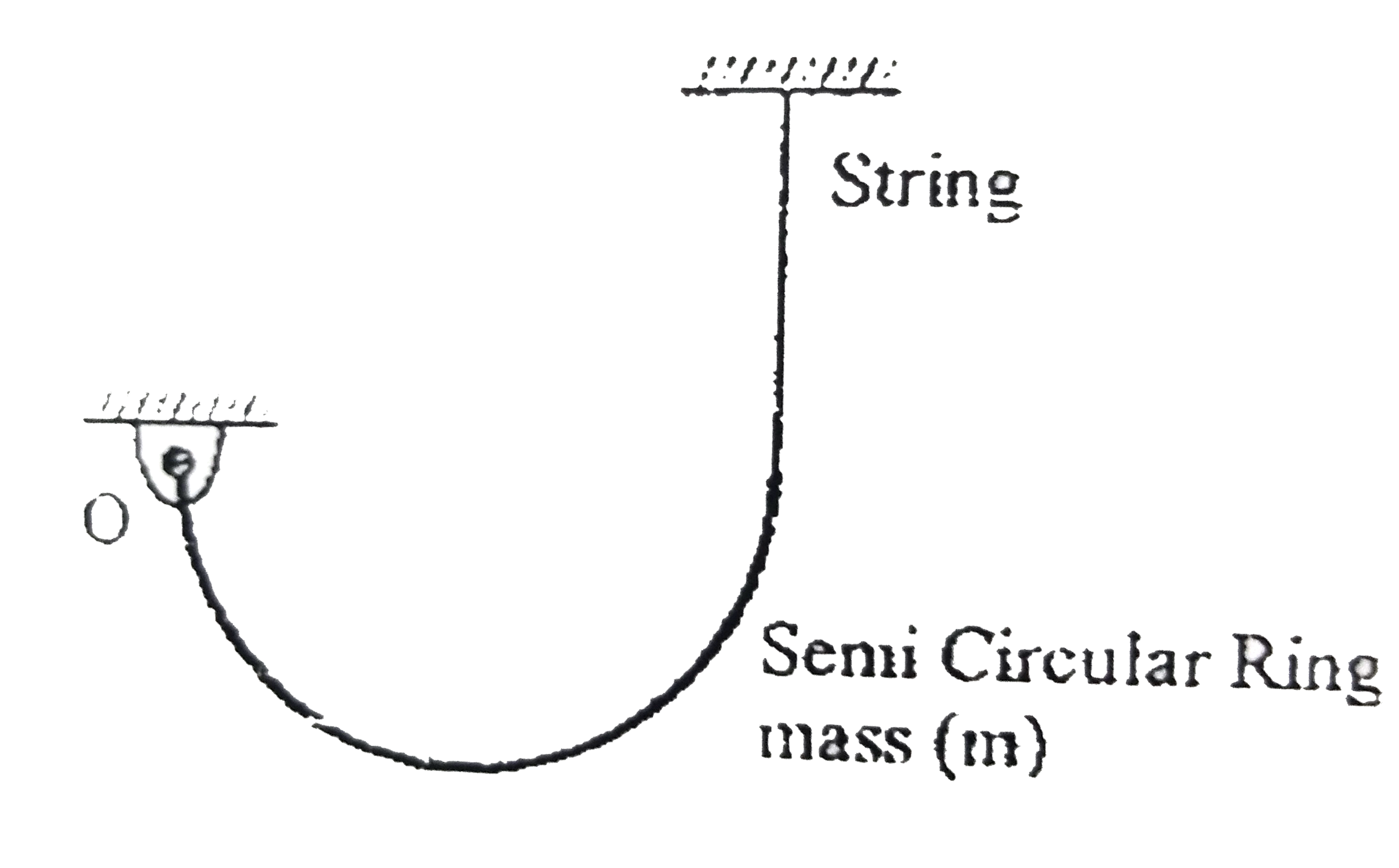
A semi-circular ring of mass m and radius R with linear charge ilensity λ, hinged at its centre. is placed in a uniform electric field as shown in the figure −1.451. Ifthe ring is slightly rotated about O and released find the time period (in sec) of oscillation. Take m=8kg,λ=2C/m and E=2N/c. Assume that coil is rotated in its own plane

The correct Answer is:6.28
Step by step video, text & image solution for A semi-circular ring of mass m and radius R with linear charge ilensity lambda, hinged at its centre. is placed in a uniform electric field as shown in the figure -1.451. Ifthe ring is slightly rotated about O and released find the time period (in sec) of oscillation. Take m = 8 kg, lambda= 2 C//m and E = 2 N//c. Assume that coil is rotated in its own plane by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Advance MCQs
40 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - Advance MCQs
33 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems
107 Videos
Similar Questions
Net electric flux through a sphere of radius 1 m placed in a uniform electric field as shown in the figure is → E = 103 N/C
View SolutionA uniform semicircular ring of mass m and radius r is hinged at end A so that it can rotate freely about end A in the vertical plane as shown in the figure. Calculate angle made by line AB with vertical in equilibrium position and time period of small oscillation of ring.

View Solution
Knowledge Check
A loop of radius R and mass m is placed in a uniform magnetic field B with its plane perpendicular to the field. Current I is flowing in it. Now loop is slightly rotated about its diameter and released. Find time period of oscillation.
A2√πmIBB√2πmIBC2√mπIBD√mπIBA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
Aλ3√3ε0RB2λ3√3ε0R2C23√3λε0RDnone the these
A uniform semicurcular ring having mass m and radius r is hanging at one of its ends freely as shown if Fig. The ring is slightly disturbed so the it oscillates in its own plane. The time period of oscillation of the ring isA2π ⎷rg(1+1π2)B2π ⎷rg(1+4π2)12C2π ⎷rg(1−2π2)12D2π ⎷2rg(1+4π)12
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View SolutionA uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
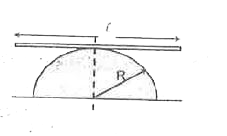
View SolutionThe semi circular ring of radius R and mass m is free to rotate about the point O in shown figure.
View SolutionThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
View Solution
