A capacitors C1 is charged to a potential V and connected to another capacitor in seris with a resistor R as shown. It is observed that heat H1 is dissipated across resistance R, tilll the circuit reaches steady state. Same process is repeated using resistance of 2R. If H2 is heat dissipated in this case then
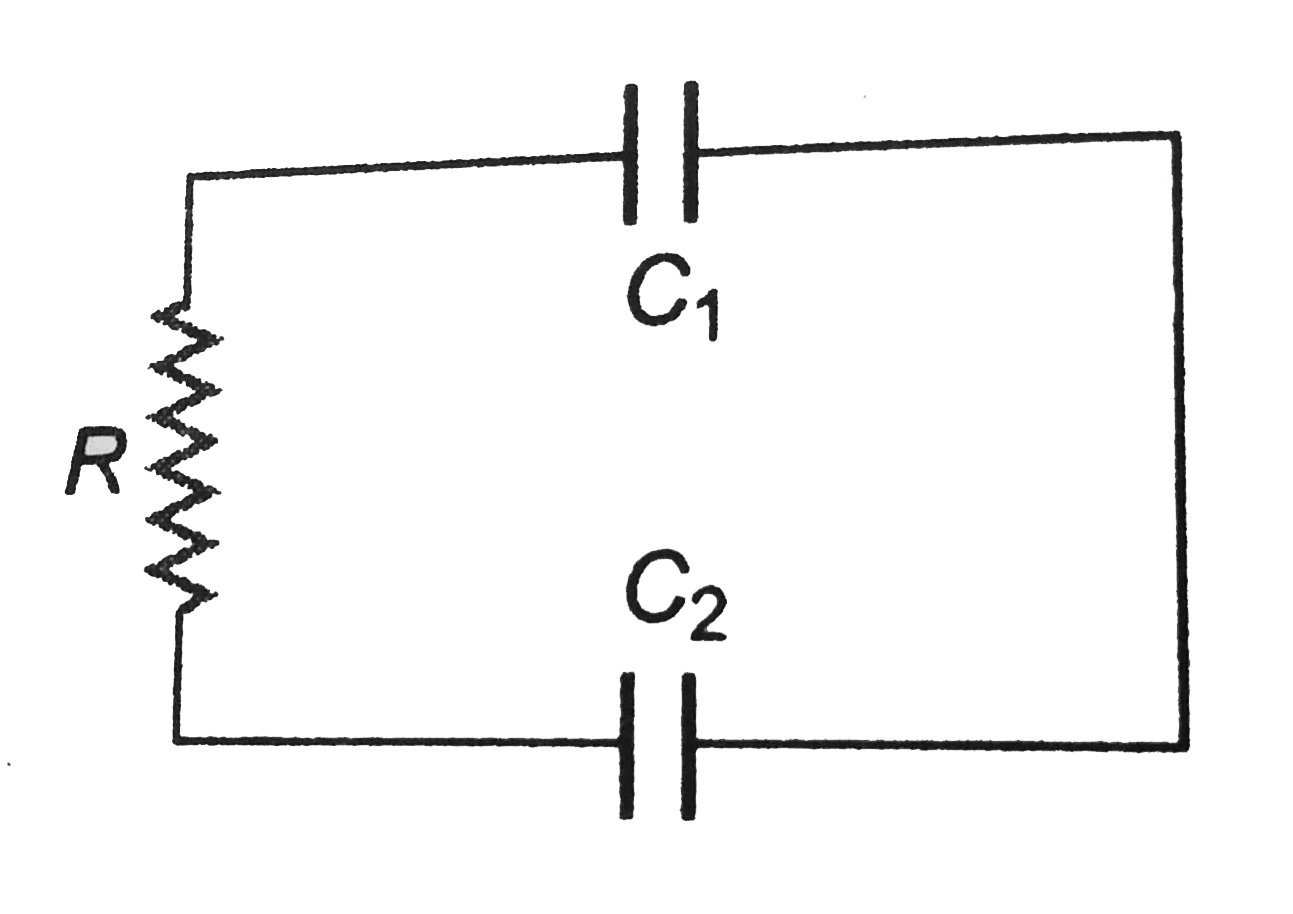
H2H1=1
H2H1=4
H2H1=14
H2H1=2
Step by step video & image solution for A capacitors C_1 is charged to a potential V and connected to another capacitor in seris with a resistor R as shown. It is observed that heat H_1 is dissipated across resistance R, tilll the circuit reaches steady state. Same process is repeated using resistance of 2R. If H_2 is heat dissipated in this case then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A capacitor is charged so that it has a stored potential energy U and then connected in series with an identical, uncharged capacitor and a resistance. Until the current in the circuit becomes negligible, the total heat wasted in the resistance is H. The ratio HU is______.
View SolutionA resistor R1 dissipates the power P when connected to a certain generator. If the resistor R2 is put in series with R1, the power dissipated by R1
View Solution
Knowledge Check
A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is VRBThe current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)CThe charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)DAfter a long time, the potential difference across the capacitor C1is(C1C1+C2)VA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
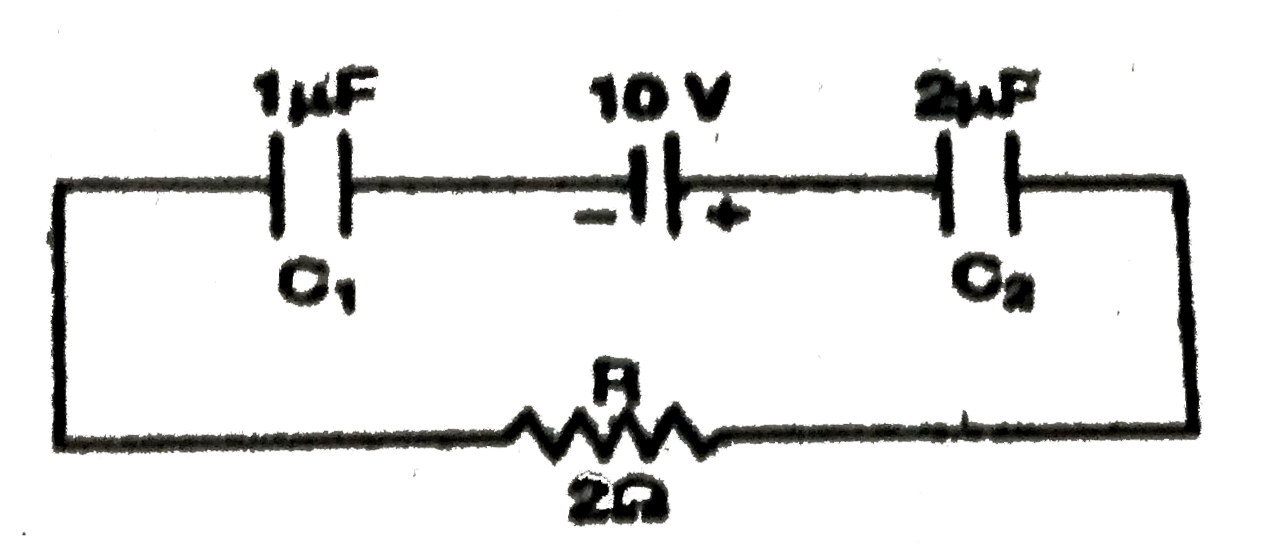 A10 VB5VC3.33 VDzero
A10 VB5VC3.33 VDzeroIn process 1, the energy stored in the capacitor EC and heat dissipated across resistance ED are related by -
AEC=EDBEC=EDin2CEC=2EDDEC=12ED
A resistor R1 dissipates the power P when connected to a certain generator. If the resistor R2 is put in series with R1, the power dissipated by R1
View SolutionTwo capacitors, having equal capacitance C, are having same charges q on each plate. They are connected across a resistor R as shown in the figure. What is the total heat generated in the resistor upto the instant when the steady state has reached
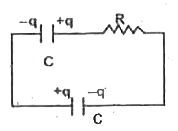
View SolutionThe power dissipated across resistance R which is connected across a battery of potential V is P. If resistance is doubled, then the power becomes
View SolutionIf the capacitors are uncharged prior to the switch being closed, the amount of heat dissipated in resistors R1 and R2 after the switch is closed would be in the ratio of
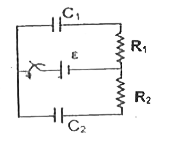
View SolutionA capacitor of capacitance 2μF is charged to a potential difference of 5V. Now, the charging battery is disconected and the capacitor is connected in parallel to a resistor of 5Ω and another unknown resistor of resistance R as shown in figure. If the total heat produced in 5Ω resistance is 10μJ then the unknown resistance R is equal to
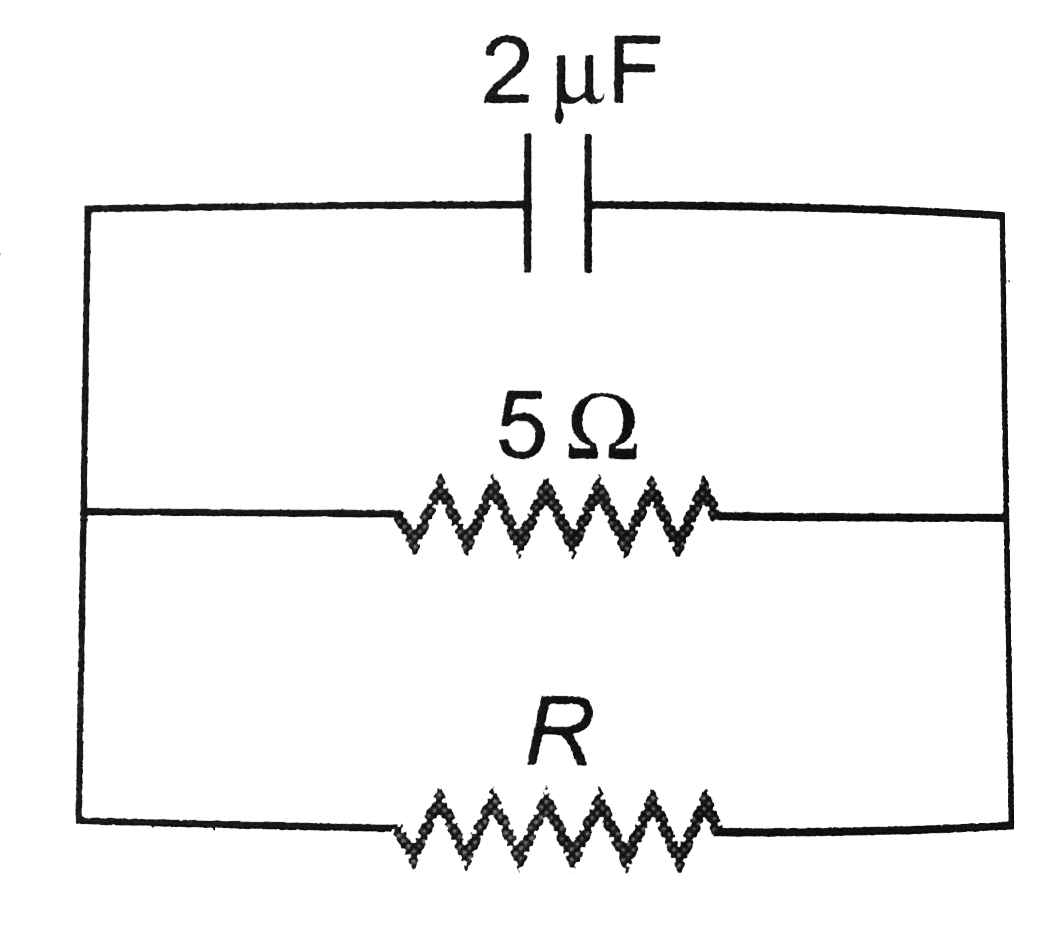
View Solution

