In a long wire of square cross-section of side length l, current density varies with distance x from one edge of cross-section as
J=aehxA/m2
Where a and b are positive constants. Find the current flowing in wire.
[alb(e−1)]
Step by step video & image solution for In a long wire of square cross-section of side length l, current density varies with distance x from one edge of cross-section as J=ae^(hx)A//m^(2) Where a and b are positive constants. Find the current flowing in wire. [(al)/(b)(e-1)] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
AB is a uniformly shaped rod of length L and cross sectional are S, but its density varies with distance from one end A of the rod as ρ=px2+c, where p and c are positive constants. Find out the distance of the centre of mass of this rod from the end A.
View SolutionA current of 4.8 A is flowing in a copper wire of cross-sectional area 3×10−4m2. Find the current density in the wire.
View Solution
Knowledge Check
A long straight wire of circular cross- section carries a current along its length. On the axis inside the wire, it follows that
Astrength of electric and magnetic fields are zeroBstrength of electric field is zero but magnetic field is non− zeroCstrength of electric and magnetic field non−zeroDstrength of electric field is non−zero but magnetic field is zero.Consider a conductor of variable cross section in which current is flowing from cross section 1 to 2. Then
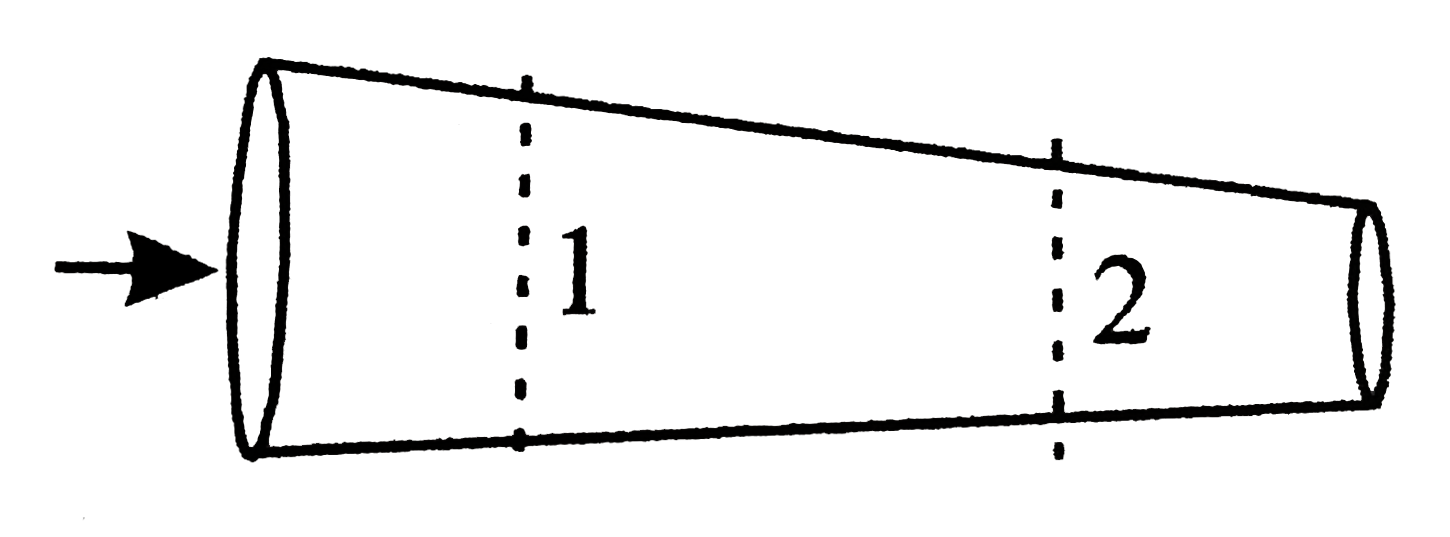 Acurrent passing through both the cross sections in the sameBcurrent through 1 is less then that through 2Cdrift velocity of electrons at 1 is less then that at 2Ddrift velocity is same at both the cross sections
Acurrent passing through both the cross sections in the sameBcurrent through 1 is less then that through 2Cdrift velocity of electrons at 1 is less then that at 2Ddrift velocity is same at both the cross sectionsThe current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
ATotal current passing through the cross-section of the wire isI=πJ0a32BTotal current passing through the cross-section of the wire isI=3πJ0a32CThe field at a distance r gt a is B=μ0J0a34rDThe field at a distance r gt a is B=μ0J0a34a
A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis
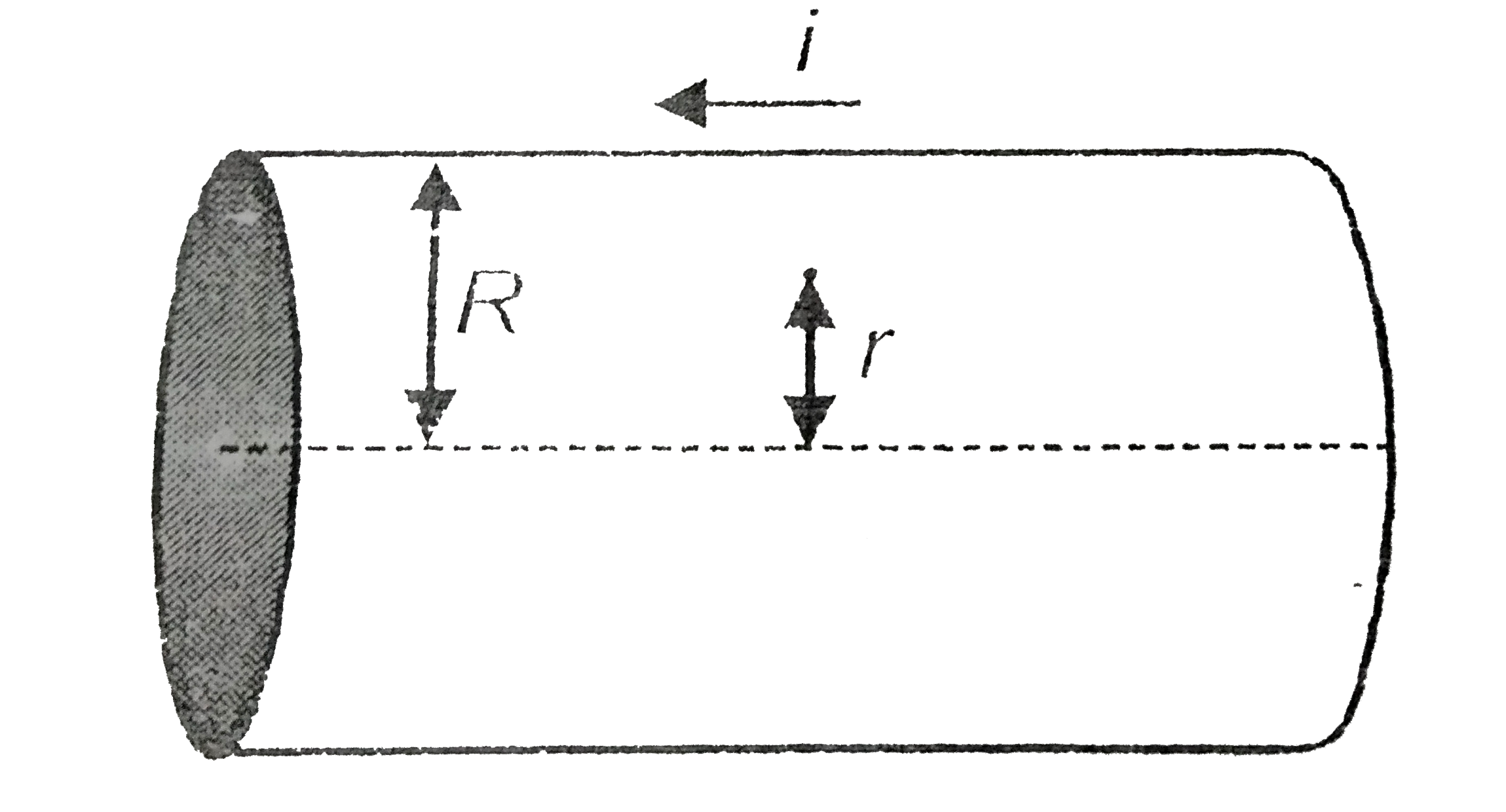
View SolutionA cylindrical wire if radius R = 2 mm is of uniform area of cross-section. The current density through a cross-section varies with radial distance r as J=ar2, where a=3.2×1011A/m2 and r is in metres. What is the current through the outer portion of the wire between radial distances R/2 and R?
View SolutionConsider a long cylindrical wire carrying current along the axis of wire. The current distributed non-uniformly on cross section. The magnetic field B inside the wire varies with distance r from the axis as B=kr4 where k is a cosntant. The current density J varies with distance r as J=crn then the value of n is (where c is another constant).
View SolutionA wire of radius R having uniform cross section in which steady current l is flowing. Then
View SolutionA copper wire has a square cross-section, 2.0 mm on a side. It carries a current of 8 A and the density of free electrons is 8×1028m−3. The drift speed of electrons is equal to
View Solution

