The relationship that exists between the electric displacement and the electric field strength in a ferroeleetric is given by the curve of primary polarization and a hysteresis loop. Are there any points on the hysteresis loop to which we might formally assign a dielectric constant equal to zero or to infinity?
Step by step video & image solution for The relationship that exists between the electric displacement and the electric field strength in a ferroeleetric is given by the curve of primary polarization and a hysteresis loop. Are there any points on the hysteresis loop to which we might formally assign a dielectric constant equal to zero or to infinity? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a certain region of space, the electric potential is V(x,y,z)=Axy−Bx2+Cy, where A, B and C are positive constants.
(a) Calculate the x, y and z- components of the electric field.
(b) At which points is the electric field equal to zero?
View SolutionAnswer question on the basis of your understanding of the following paragraph and the related studied concepts.
Eletric field around a single charges or a charges configuration can be pictorially mapped by drawing electric field lines in space. An electric field line is, in general, a curve drawn in such a way that the tangent to it at each point is in the direction of the net. field point. An arrow on the curve is obviously necessary to specify the direction of electric field from the two possible directions indicated by a tangent to the curve. A field line is a space curve i.e., a curve in three dimensions.
Electric field lines may be taken to be continous curve without any breaks. Relative density (i.e. closeness) of the field lines at different points indicate the relative strength of electric field at those points. The field lines crowd where the field is strong and are spaced apart where it is weak.
Can electrostatic field lines from closed loops?Why
View Solution
Knowledge Check
A parallel plate capacitor is connected to a battery of constant emf. Let the electric field at a given point between the plate be E0, when there is no medium between the plates. The new electric field at the point, If a medium of dielectric constant A is intoduced between them, is
AE04BE02CE0D4E0Following experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
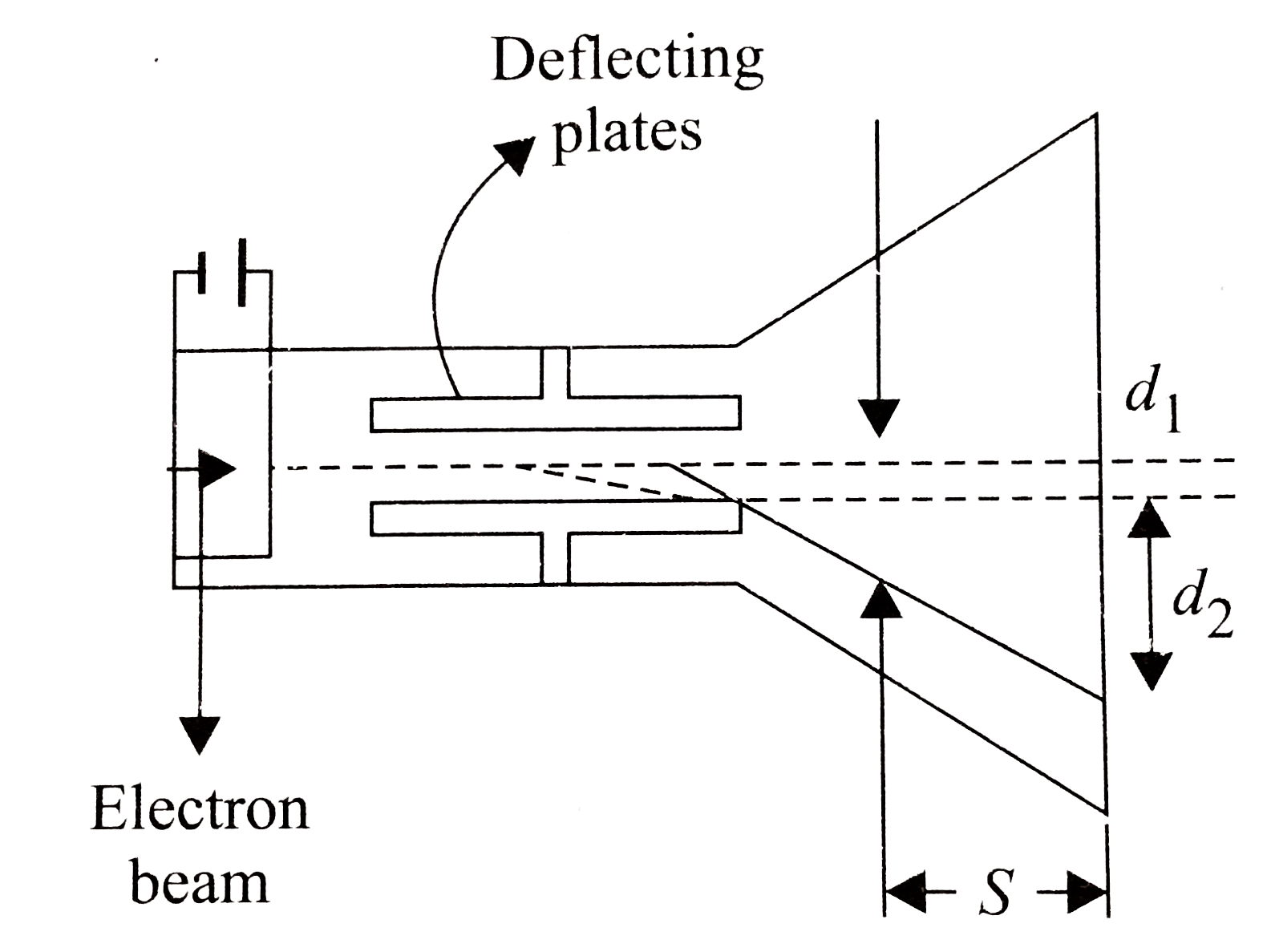
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experimentAThe electric field point to the top, while the magnetic field point into the pageBThe electric field point to the top, while the magnetic field point out of pageCElectric field points to the bottom, while the magnetic field point out of pateDElectric field points to the bottom, while the magnetic field points into the pageSix loops are formed of copper wire of the same cross-sectional area. Loops 1,2,3 and 4 are identical, loop 5 has the same area as the others but is longer. At the instant shown, all the loops are moving at the same speed in the directions indicated. A uniform and constant magnetic field points out of the page in region I, in region II there is no magnetic field. Ignore any interaction between the loops.
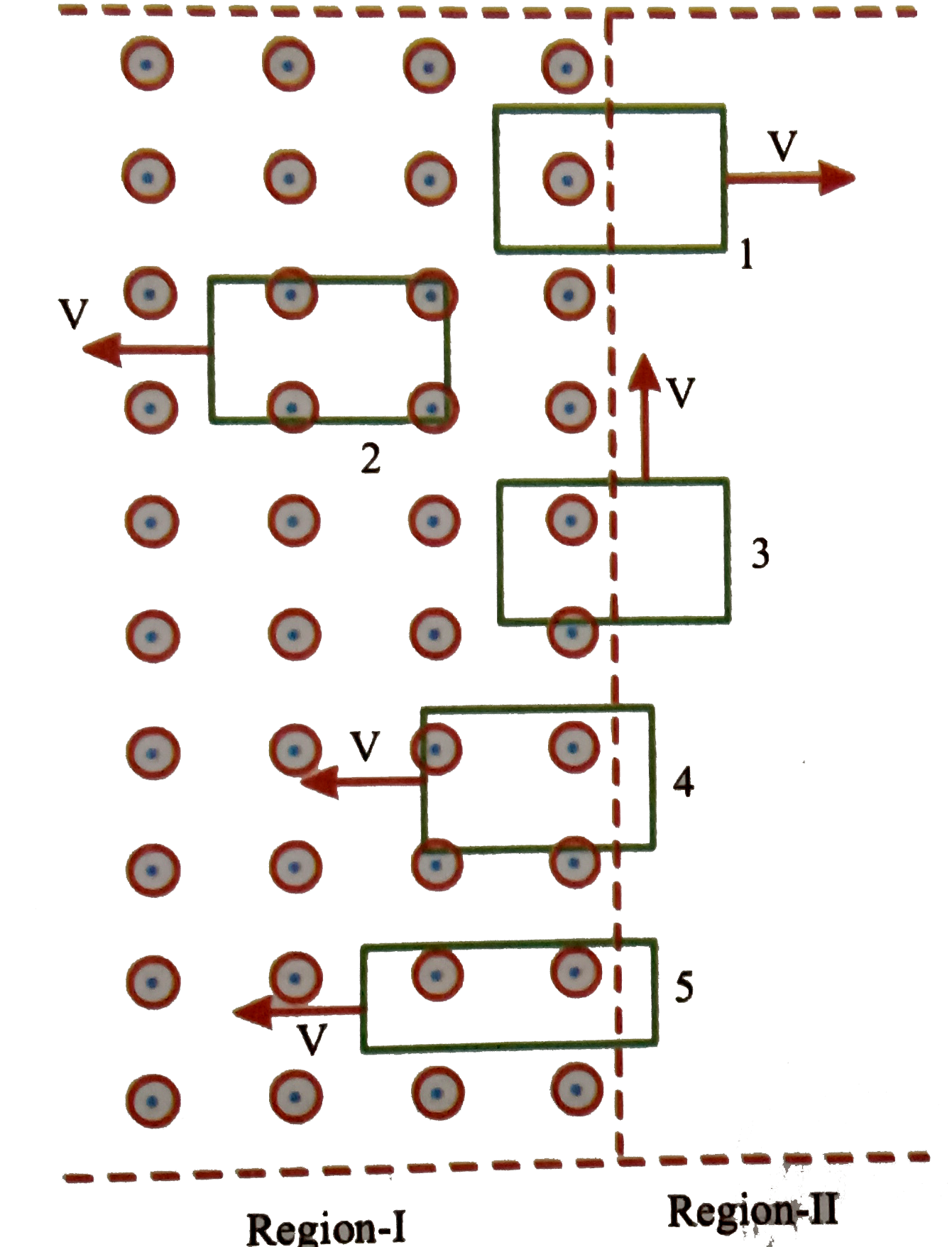
Then the number of loop or loops in which current is nonzero and in clockwise directionAno loopBone loopCtwo loopsDThree loops
On the basis of your understanding of the following paragraph and the related studied concepts.
An electric dipole is a pair of equal and opposite point charges q and -9 separated by a distance '2a'. The total charge of the electric dipole is obviously zero but the field of the electric dipole at a point is non-zero because electric fields due to + qand - q charges at the point do not exactly cancel out. Electric field of a dipole, at large distances, depends on the product 'qa'. So we define a term dipole moment vector →p of an electric dipole as →p=q(2a) and its direction is along the line from q to + q charge. The dipole field at large distances fall off as 1r3. Further, the magnitude and direction of the dipole field depends not only on the distance r but also on the angle between the position vector →r and the dipole moment →p.
Concept of electric dipoles is very significant for different materials. In most molecules, the centres of positive charges and of negative charges exactly coincide and their dipole moment is zero. However they develop a dipole moment when an electric field as applied. Such molecules are termed non-polar molecules. But in some molecules, the centres of positive charges do not exactly coincide with that of negative charges and the molecules has a permanent dipole moment even in the absence of an electric field. Such molecules are called polar molecules. Various materials give rise to interesting properties and important applications in the presence or absence of electric field.
What do you mean by polarisation of a dielectric ?
View SolutionSix point charges , each of the same magnitude q, are arranged in different manners as shown in Column II . In each case, a point M and a line PQ passing through M are shown . Let E be the electric field and V be the electric potential at M (potential at infinity is zero ) due to the given charge distribution when it is at rest . Now, the whole system is set into rotation with a constant angular velocity about the line PQ . Let B be the magnetic field at M and μ be the magnetic moment of the system in this condition . Assume each rotating charge to be equivalent to a steady current .

View SolutionAn infinite plane of uniform dielectric with permittivity ε is uniformly charged with extraneous chagre fo space density ρ. The thickness of the plate is equal to 2d. Find:
(a) the magnitude of the electric field strength and the potential as functions of distance l from the middle point of the plane.(where the potential is assumed to be equal to zero), having chosen teh x coriditnate axis perpendicular to the plate, draw the approximate plots of teh projection Ex(x) of the vector E and the potentail φ(x), plots fo the projection Ex(x) of the vector E adn the potential φ(x),
(b) the surface and space denstites of the bound charge.
View SolutionAssertion: No net charge can exist in the region where electric field is uniform.
Reason: For any type of Gaussian surface selected within the region of a uniform electric field, the angle between electric field intensity and area normal is 90∘ everywhere. Hence, electric flux linked with the selected Gaussian surface is equal to zero. If the net electric flux is zero for some Gaussian surface then according to Gauss's law the net charge enclosed within the surface must be zero.
View SolutionConsider the following statements.
I The magnetic field lines of a magnet (or a solenoid) form continuous closed loops. This is unlike the electric dipole where these field lines begin from a positive charge and end on the negative charge or escape to infinity.
II The tangent to the field line at a given point represents the direction of the net magnetic field B at that point.
III. The larger the number of field lines crossing per unit area, the stronger the magnitude of the magnetic field B.
IV. The magnetic field lines intersect each other. Which of the following statements are correct?
View Solution
