Assertion: No net charge can exist in the region where electric field is uniform.
Reason: For any type of Gaussian surface selected within the region of a uniform electric field, the angle between electric field intensity and area normal is 90∘ everywhere. Hence, electric flux linked with the selected Gaussian surface is equal to zero. If the net electric flux is zero for some Gaussian surface then according to Gauss's law the net charge enclosed within the surface must be zero.
If both assertion and reason are correct and reason is a correct explanation of the assertion .
If both assertion and reason are correct but reason is not the correct explanation of assertion
If assertion is correct but reason is incorrect
If assertion is incorrect but reason is correct.
The correct Answer is:C
To solve the given question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
The assertion states that "No net charge can exist in the region where the electric field is uniform." A uniform electric field means that the electric field has the same magnitude and direction at every point in that region.
2. Applying Gauss's Law:
According to Gauss's Law, the electric flux (Φ) through a closed surface is proportional to the charge (Q) enclosed within that surface:
Φ=Qinϵ0
where ϵ0 is the permittivity of free space.
3. Electric Flux in a Uniform Electric Field:
If we consider a Gaussian surface in a uniform electric field, the electric field lines will enter and exit the surface. For a closed surface in a uniform electric field, the amount of electric field lines entering the surface will equal the amount exiting, leading to a net electric flux of zero:
Φnet=Φin−Φout=0
4. Conclusion from Gauss's Law:
Since the net electric flux is zero, according to Gauss's Law, the net charge enclosed within the Gaussian surface must also be zero:
Qin=0
This supports the assertion that no net charge can exist in a region with a uniform electric field.
5. Understanding the Reason:
The reason states that "For any type of Gaussian surface selected within the region of a uniform electric field, the angle between electric field intensity and area normal is 90 degrees everywhere." This is incorrect because, while the electric field may be uniform, it does not necessarily mean that the angle between the electric field and the area vector (normal) of the surface is always 90 degrees. For example, in the case of a cylindrical surface aligned with the electric field, the lateral surface has an angle of 0 degrees with the electric field.
6. Final Evaluation:
The assertion is correct, but the reason is incorrect. Therefore, the correct answer is:
- Assertion is true, Reason is false.
Final Answer:
The assertion is correct, but the reason is incorrect. Thus, the answer is C.
The assertion states that "No net charge can exist in the region where the electric field is uniform." A uniform electric field means that the electric field has the same magnitude and direction at every point in that region.
According to Gauss's Law, the electric flux (Φ) through a closed surface is proportional to the charge (Q) enclosed within that surface:
Φ=Qinϵ0
where ϵ0 is the permittivity of free space.
If we consider a Gaussian surface in a uniform electric field, the electric field lines will enter and exit the surface. For a closed surface in a uniform electric field, the amount of electric field lines entering the surface will equal the amount exiting, leading to a net electric flux of zero:
Φnet=Φin−Φout=0
Since the net electric flux is zero, according to Gauss's Law, the net charge enclosed within the Gaussian surface must also be zero:
Qin=0
This supports the assertion that no net charge can exist in a region with a uniform electric field.
The reason states that "For any type of Gaussian surface selected within the region of a uniform electric field, the angle between electric field intensity and area normal is 90 degrees everywhere." This is incorrect because, while the electric field may be uniform, it does not necessarily mean that the angle between the electric field and the area vector (normal) of the surface is always 90 degrees. For example, in the case of a cylindrical surface aligned with the electric field, the lateral surface has an angle of 0 degrees with the electric field.
The assertion is correct, but the reason is incorrect. Therefore, the correct answer is:
- Assertion is true, Reason is false.
The assertion is correct, but the reason is incorrect. Thus, the answer is C.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (Matching ) )
Explore 1 Video
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (Matrix))
Explore 2 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:COMPETITION FILE ( Objective Question (D.MCQ) Passage )
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
Knowledge Check
The electric flux through a closed Gaussian surface depends upon
Anet charge enclosed and permittivity of the medium.Bnet charge enclosed, permittivity of the medium and the size of the Gaussian surface.Cet charge enclosed only.Dpermittivity of the medium only.The Gaussian surface needed for calculating the electric field due to a charge distribution is
Aany surface around the charge distributionBonly spherical surface.Cany closed surface around the charge.Donly cylindrical surface.Assertion : In a cavity within a conductor, the electric field is zero.
Reason : Charges in a conductor reside only at its surface.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reasonb is falseDIf both assertion and reason are false.
Which of the following is true for electric flux through a Gaussian surface ?
View SolutionThe position of the point where the net electric field will be zero is
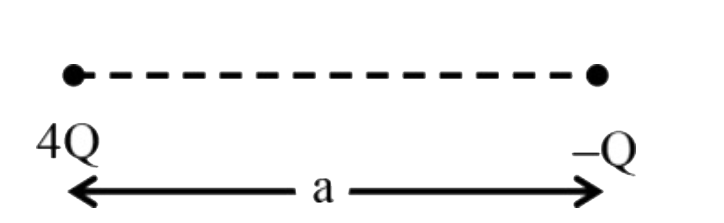
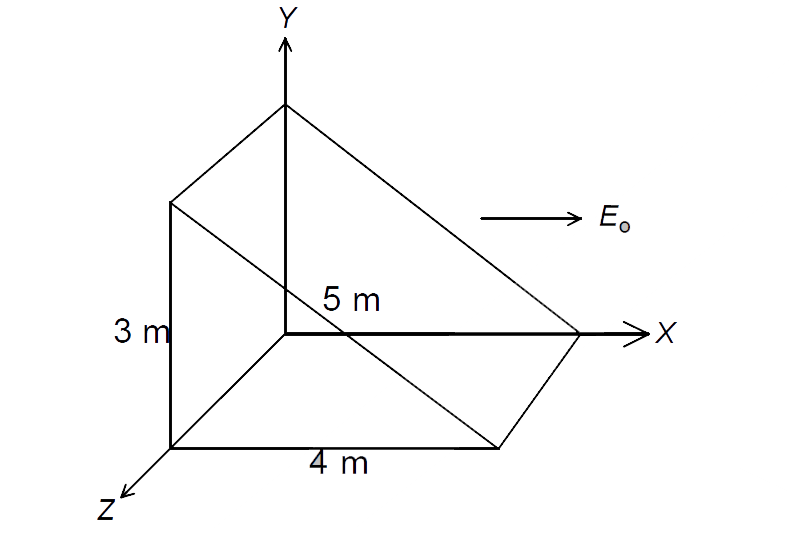
View SolutionThe wedge-shaped surface in figure is in a region of uniform electric field E0 along x axis. The net electric flux for the entire closed surface is -
View SolutionAssertion : If a dipole is enclosed by a surface, then according to Gauss's law, electric flux linked with it will be zero.
Reason : The charge enclosed by a surface is zero.
View SolutionIf the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
View Solution

